Навигация
Правую часть равенства всегда можно сделать неотрицательной , умножая оби части на -1
2. Правую часть равенства всегда можно сделать неотрицательной , умножая оби части на -1 .
Например равенство X1 - 2X2 - S2 = 0 эквивалентно равенству - X1 + 2X2 + S2 = 0
3. Знак неравенства изменяется на противоположный при умножении обеих частей на -1 .
Например можно вместо 2 < 4 записать - 2 > - 4 , неравенство X1 - 2X2 <= 0 заменить на - X1 + 2X2 => 0
Переменные
Любую переменную Yi , не имеющую ограничение в знаке , можно представить как разность двух неотрицательных переменных :
Yi=Yi’-Yi’’, где Yi’,Yi’’=>0.
Такую подстановку следует использовать во всех ограничениях , которые содержат исходную переменную Yi , а также в выражении для целевой функции .
Обычно находят решение задачи ЛП , в котором фигурируют переменные Yi’ и Yi’’ , а затем с помощью обратной подстановки определяют величину Yi . Важная особенность переменных Yi’ и Yi’’ состоит в том , что при любом допустимом решении только одна из этих переменных может принимать положительное значение , т.е. если Yi’>0 , то Yi’’=0, и наоборот . Это позволяет рассматривать Yi’ как остаточную переменную , а Yi’’ - как избыточную переменную , причем лишь одна из этих переменных может принимать положительное значение . Указанная закономерность широко используется в целевом программировании и фактически является предпосылкой для использования соответсвующих преобразований в задаче 2.30
Целевая функция
Целевая функция линейной оптимизационной модели , представлена в стандартной форме , может подлежать как максимизации , так и минимизации . В некоторых случаях оказывается полезным изменить исходную целевую функцию .
Максимизация некоторой функции эквивалентна минимизации той же функции , взятой с противоположным знаком , и наоборот . Например максимизация функции
Z = X1 + 25X2
эквивалентна минимизации функции
( -Z ) = -X1 - 25X2
Эквивалентность означает , что при одной и той же совокупности ограничений оптимальные значения X1 , X2 , в обоих случаях будут одинаковы . Отличие заключается только в том , что при одинаковых числовых значениях целевых функций их знаки будут противоположны .
Симплекс-метод .
В вычислительной схеме симплекс-метода реализуется упорядоченный процесс , при котором , начиная с некоторой исходной допустимой угловой точки ( обычно начало координат ) , осуществляются последовательные переходы от одной допустимой экстремальной точки к другой до тех пор , пока не будет найдена точка , соответствующая оптимальному решению .
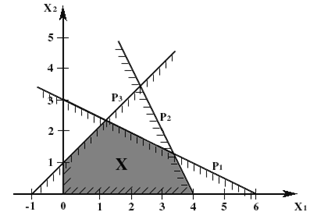
Общую идею симплекс-метода можно проиллюстрировать на примере модели , посроенной для нашей задачи . Пространство решений этой задачи представим на рис. 1 . Исходной точкой алгоритма является начало координат ( точка А на рис. 1 ) . Решение , соответствующее этой точке , обычно называют начальным решением . От исходной точки осуществляется переход к некоторой смежной угловой точке .
Выбор каждой последующей экстремальной точки при использовании симплекс-метода определяется следующими двумя правилами .
1. Каждая последующая угловая точка должна быть смежной с предыдущей . Этот переход осуществляется по границам ( ребрам ) пространства решений .
2. Обратный переход к предшествующей экстремальной точке не может производиться .
Таким образом , отыскание оптимального решения начинается с некоторой допустимой угловой точки , и все переходы осуществляются только к смежным точкам , причем перед новым переходом каждая из полученных точек проверяется на оптимальность .
Определим пространство решений и угловые точки агебраически . Требуемые соотнощшения устанавливаются из указанного в таблице соответствия геометрических и алгебраических определений
.
| Геометрическое определение | Алгебраическое определение ( симплекс метод ) |
| Пространство решений | Ограничения модели стандартной формы |
| Угловые точки | Базисное решение задачи в стандартной форме |
Представление пространства решений стандартной задачи линейного программирования .
Линейная модель , построенная для нашей задачи и приведенная к стандартной форме , имеет следующий вид :
Максимизировать
Z = X1 + 25X2 + 0S1 + 0S2
При ограничениях
5X1 + 100X2 + S1 = 1000
- X1 + 2X2 + S2 = 0
X1=>0 , X2=>0 , S1=>0 , S2=>0
Каждую точку пространства решений данной задачи , представленную на рис.1 , можно определить с помощью переменных X1 , X2 , S1 и S2 , фигурирующими в модели стандартной формы. При S1 = 0 и S2 = 0 ограничения модели эквивалентны равенствам , которые представляются соответствующими ребрами пространства решений . Увеличение переменных S1 и S2 будет соответствовать смещению допустимых точек с границ пространства решений в его внутреннюю область. Переменные X1 , X2 , S1 и S2 , ассоциированные с экстремальными точками А , В , и С можно упорядочить , исходя из того , какое значение ( нулевое или ненулевое ) имеет данная переменная в экстремальной точке .
| Экстремальная точка | Нулевые переменные | Ненулевые переменные |
| А | S2 , X2 | S1 , X1 |
| В | S1 , X2 | S2 , X1 |
| С | S1 , S2 | X1 , X2 |
Анализируя таблицу , легко заметить две закономерности:
1. Стандартная модель содержит два уравнения и четыре
неизвестных , поэтому в каждой из экстремальных точек две ( = 4 - 2 ) переменные должны иметь нулевые значения .
2. Смежные экстремальные точки отличаются только одной пе-
ременной в каждой группе ( нулевых и ненулевых переменных ) ,
Первая закономерность свидетельствует о возможности опре-
деления экстремальных точек алгебраическим способом путем при-
равнивания нулю такого количества переменных , которое равно
разности между количеством неизвестных и числом уравнений .
В этом состоит сущность свойства однозначности экстремальных
точе на рис 1 каждой неэкстремальной точке соответствует
не более одной нулевой переменной . Так , любая точка внутренней
области пространства решений вообще не имеет ни одной нулевой
переменной, а любая неэкстремальная точка , лежащая на границе ,
всегда имеет лишь одну нулевую переменную .
Свойство однозначности экстремальных точек позволяет опре-
делить их алгебраическим методом. Будем считать , что линейная
модель стандартной формы содержит т уравнений и п ( т <= п ) не-
известных ( правые части ограничений — неотрицательные ) . Тогда
все допустимые экстремальные точки определяются как все одно-
значные неотрицательные решения системы m уравнений , в ко-
торых п — m переменных равны нулю.
Однозначные решения такой системы уравнений, получаемые
путем приравнивания к нулю ( п — т ) переменных , называются
базисными решениями . Если базисное решение удовлетворяет
требованию неотрицательности правых частей , оно называется
допустимым базисным решением. Переменные , имеющие нулевое
значение , называются небазисными переменными , остальные —
базисными переменными.
Из вышеизложенного следует , что при реализации симплекс-
метода алгебраическое определение базисных решений соответст-
вует идентификации экстремальных точек , осуществляемой при
геометрическом представлении пространства решений . Таким об-
разом , максимальное число итераций при использовании симплекс-
метода равно максимальному числу базисных решений задачи ЛП ,
представленной в стандартной форме . Это означает , что количество
итерационных процедур симплекс-метода не превышает
Cпт= n! / [ ( n - m )!m! ]
Вторая из ранее отмеченных закономерностей оказывается
весьма полезной для построения вычислительных процедур симп-
лекс-метода , при реализации которого осуществляется последова-
тельный переход от одной экстремальной точки к другой, смежной с ней . Так как смежные экстремальные точки отличаются только
одной переменной, можно определить каждую последующую ( смеж-
ную) экстремальную точку путем замены одной из текущих не-
базисных ( нулевых ) переменных текущей базисной переменной.
В нашем случае получено решение , соответствующее точке А , откуда следует осуществить переход в точку В . Для этого нужно увеличивать небазисную переменную X2 от исходного нулевого значения до значе-
ния , соответствующего точке В ( см. рис. 1 ). В точке B переменная
S1 ( которая в точке А была базисной ) автоматически обращается в
нуль и , следовательно , становится небазисной переменной . Таким
образом , между множеством небазисных и множеством базисных
переменных происходит взаимообмен переменными X2 и S1 . Этот
процесс можно наглядно представить в виде следующей таблицы.
| Экстремальная точка | Нулевые переменные | Ненулевые переменные |
| А | S2 , X2 | S1 , X1 |
| В | S1 , X2 | S2 , X1 |
Применяя аналогичную процедуру ко всем экстремальным точкам
рис. 1 , можно убедиться в том , что любую последующую экстре-
мальную точку всегда можно определить путем взаимной замены
по одной переменной в составе базисных и небазисных переменных
( предыдущей смежной точки ) . Этот фактор существенно упрощает
реализацию вычислительных процедур симплекс-метода.
Рассмотренный процесс взаимной замены переменных приводит
к необходимости введения двух новых терминов . Включаемой пе-
ременной называется небазисная в данный момент переменная ,
которая будет включена в множество базисных переменных на сле-
дующей итерации ( при переходе к смежной экстремальной точке ) .
Исключаемая переменная — это та базисная переменная , которая
на следующей итерации подлежит исключению из множества ба-
зисных переменных .
Вычислительные процедуры симплекс-метода .
симплекс-алгоритм состоит из следующих шагов.
Шаг 0. Используя линейную модель стандартной формы , опреде-
ляют начальное допустимое базисное решение путем приравнива-
ния к нулю п — т ( небазисных ) переменных.
Шаг 1. Из числа текущих небазисных ( равных нулю ) перемен-
ных выбирается включаемая в новый базис переменная , увеличение
которой обеспечивает улучшение значения целевой функции. Если
такой переменной нет , вычисления прекращаются , так как текущее
базисное решение оптимально . В противном случае осуществляется
переход к шагу 2.
Шаг 2. Из числа переменных текущего базиса выбирается исклю-
чаемая переменная , которая должна принять нулевое значение ( стать
небазисной ) при введении в состав базисных новой переменной .
Шаг 3. Находится новое базисное решение , соответствующее
новым составам небазисных и базисных переменных . Осуществляется переход к шагу 1.
Поясним процедуры симплекс-метода на примере решения нашей зада-
чи . Сначала необходимо представить целевую функцию и ограничения модели в стандартной форме:
Z - X1 - 25X2 +0S1 -0S2 = 0 ( Целевая функция )
5X1 + 100X2 + S1 = 1000 ( Ограничение )
-X1 + 2X2 + S2 = 0 ( Ограничение )
Как отмечалось ранее , в качестве начального пробного решения
используется решение системы уравнений , в которой две переменные принимаются равными нулю . Это обеспечивает единст-
венность и допустимость получаемого решения . В рассматриваемом
случае очевидно, что подстановка X1 = X2 = 0 сразу же приводит к следующему результату: S1 = 1000 , S2 = 0 ( т. е. решению , соответствующему точке А на рис. 1 ) . Поэтому точку А можно использовать как начальное допустимое решение . Величина Z в этой точке равна нулю , так как и X1 и X2 имеют нулевое значение . Поэтому , преобразовав уравнение целевой функции так , чтобы его правая часть стала равной нулю , можно убедиться в том , что правые части уравнений целевой функции и ограничений полностью характеризуют начальное решение . Это имеет место во всех случаях , когда начальный базис состоит из остаточных переменных.
Полученные результаты удобно представить в виде таблицы :
| Базисные переменные | Z | X1 | X2 | S1 | S2 | Решение | |
| Z | 1 | -1 | - 25 | 0 | 0 | 0 | Z – уравнение |
| S1 | 0 | 5 | 100 | 1 | 0 | 1000 | S1 –уравнение |
| S2 | 0 | -1 | 2 | 0 | 1 | 0 | S2 – уравнение |
Эта таблица интерпретируется следующим образом. Столбец
« Базисные переменные » содержит переменные пробного базиса S1 ,
S2 , значения которых приведены в столбце « Решение » . При
этом подразумевается , что небазисные переменные X1 и X2 ( не пред-
ставленные в первом столбце ) равны нулю . Значение целевой функ-
ции Z = 1*0 + 25*0 + 0*1000 + 0*1 равно нулю , что и показано в последнем столбце таблицы .
Определим , является ли полученное пробное решение наи-
лучшим ( оптимальным ) . Анализируя Z - уравнение , нетрудно заме-
тить , что обе небазисные переменные X1 и X2 , равные нулю , имеют
отрицательные коэффициенты . Всегда выбирается переменная с большим абсолютным значением отрицательного коэффициента ( в Z - уравнении ) , так как практический опыт вычислений показывает , что в этом случае оптимум достигается быстрее .
Это правило составляет основу используемого в вычислительной
схеме симплекс-метода условия оптимальности , которое состоит в
том , что , если в задаче максимизации все небазисные переменные в
Z - Уравнение имеют неотрицательные коэффициенты , полученное пробное решение является оптимальным . В противном случае в ка-
честве новой базисной переменной следует выбрать ту , которая имеет
наибольший по абсолютной величине отрицательный коэффициент .
Применяя условие оптимальности к исходной таблице , выберем
в качестве переменной , включаемой в базис , переменную Х2 . Исклю-
чаемая переменная должна быть выбрана из совокупности базисных
переменных S1 , S2 . Процедура выбора исключаемой переменной предполагает проверку условия допустимости , требующего , чтобы в качестве исключаемой переменной выбиралась та из пере-
менных текущего базиса , которая первой обращается в нуль при уве-
личении включаемой переменной X2 вплоть до значения , соответствующего смежной экстремальной точке .
Интересующее нас отношение ( фиксирующее искомую точку пе-ресечения и идентифицирующее исключаемую переменную ) можно
определить из симплекс-таблицы. Для этого в столбце , соответствующем вводимой переменной X2 , вычеркиваются отрицательные и нулевые элементы ограничений . Затем вычисляются отношения постоянных , фигурирующих в правых частях этих ограничений , к оставшимся элементам столбца , соответствующего вводимой переменной X2 . Исключаемой переменной будет та переменная текущего базиса , для которой указанное выше отношение минимально.
Начальная симплекс-таблица для нашей задачи , получаемая после проверки условия допустимости ( т. е. после вычисления соответствующих отношений и определения исключаемой переменной ) , воспроизведена ниже . Для удобства описания вычислительных процедур , осуществляемых на следующей итерации , введем ряд необходимых определений . Столбец симплекс-таблицы , ассоциированный с вводимой переменной , будем называть ведущим столбцом . Строку , соответствующую исключаемой переменной , назовем ведущей строкой ( уравнением ) , а элемент таблицы , находящийся на пересечении ведущего столбца и ведущей строки , будем называть ведущим элементом .
После того как определены включаемая и исключаемая пере-
менные ( с использованием условий оптимальности и допустимости ) ,
следующая итерация ( поиск нового базисного решения ) осуществля-
ется методом исключения переменных , или методом Гаусса — Жордана . Этот процесс изменения базиса включает вычислительные процедуры двух типов .
Тип 1 ( формирование ведущего уравнения ) .
Новая ведущая строка = Предыдущая ведущая строка / Ведущий элемент
Тип 2 ( формирование всех остальных уравнений , включая Z - yравнение ) .
Новое уравнение = Предыдущее уравнение —
é Коэффициент ù
ê ведущего столбца ê * ( Новая ведущая строка ) .
ê предыдущего ê
ë уравнения û
Выполнение процедуры типа 1 приводит к тому , что в новом
ведущем уравнении ведущий элемент становится равным единице .
В результате осуществления процедуры типа 2 все остальные коэф-
фициенты , фигурирующие в ведущем столбце , становятся равными
нулю . Это эквивалентно получению базисного решения путем ис-
ключения вводимой переменной из всех уравнений , кроме ведущего .
Применяя к исходной таблице процедуру 1 , мы делим S2 - уравнение на ведущий элемент , равный 1 .
| Базисные переменные | Z | X1 | X2 | S1 | S2 | Решение |
| Z | ||||||
| S1 | ||||||
| S2 | 0 | -1/2 | 1 | 0 | 1/2 | 0 |
Чтобы составить новую симплекс-таблицу , выполним необходимые вычислительные процедуры типа 2 .
Похожие работы
... соответствующее этой точке, обычно называют начальным решением. От исходной точки осуществляется переход к некоторой смежной угловой точке. Выбор каждой последующей экстремальной точки при использовании симплекс-метода определяется следующими двумя правилами. Каждая последующая угловая точка должна быть смежной с предыдущей. Этот переход осуществляется по границам ( ребрам ) пространства решений ...
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
... 0 505/103 0 792/103 669/103 500/103 Анализ Таблицы 6 позволяет сделать вывод о допустимости и оптимальности базиса XБ4=(x5, x7, x1, x2, x4)T. 3.4 Результат решения задачи планирования производства В результате решения поставленной задачи симплекс-методом получили набор производимой продукции x=(x1, x2, x3, x4, x5)=( 15145/103, 8910/103, 0, 1250/103, 3255/103), который удовлетворяет всем ...
... на t3 часов. Прибыль от реализации единицы готового изделия А составляет a рублей, а изделия В - b рублей. Составить план производства изделий А и В, обеспечивающий максимальную прибыль от их реализации. Решить задачу простым симплекс-методом. Дать геометрическое истолкование задачи, используя для этого её формулировку с ограничениями-неравенствами. а1 = 1 b1 = 5 t1 = 10 a = 2 а2 = 3 b2 = 2 t2 ...
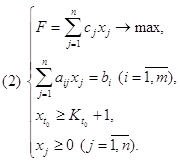
0 комментариев