Навигация
Построение математической модели
3 Построение математической модели
3.1 Корреляционный анализ.
Для оценки степени зависимости между переменными модели построим корреляционную матрицу, и для каждого коэффициента корреляции в матрице рассчитаем V-функцию, которая служит для проверки гипотезы об отсутствии корреляции между переменными.
Таблица 3.1. – Корреляционная матрица
| Y | X1 | X2 | X3 | X4 | X5 | ||
| Y | R | 0,95238 | 0,00950 | 0,21252 | -0,01090 | -0,30012 | -0,42102 |
| V | 8,30380 | 0,04247 | 0,96511 | -0,04873 | -1,38479 | -2,00769 | |
| X1 | R | 0,00950 | 0,95238 | 0,36487 | 0,13969 | 0,50352 | -0,12555 |
| V | 0,04247 | 8,30380 | 1,71054 | 0,62883 | 2,47761 | -0,56445 | |
| X2 | R | 0,21252 | 0,36487 | 0,95238 | 0,23645 | 0,06095 | -0,19187 |
| V | 0,96511 | 1,71054 | 8,30380 | 1,07781 | 0,27291 | -0,86885 | |
| X3 | R | -0,01090 | 0,13969 | 0,23645 | 0,95238 | 0,24228 | 0,25014 |
| V | -0,04873 | 0,62883 | 1,07781 | 8,30380 | 1,10549 | 1,14293 | |
| X4 | R | -0,30012 | 0,50352 | 0,06095 | 0,24228 | 0,95238 | -0,03955 |
| V | -1,38479 | 2,47761 | 0,27291 | 1,10549 | 8,30380 | -0,17694 | |
| X5 | R | -0,42102 | -0,12555 | -0,19187 | 0,25014 | -0,03955 | 0,95238 |
| V | -2,00769 | -0,56445 | -0,86885 | 1,14293 | -0,17694 | 8,30380 |
Гипотеза о нулевой корреляции принимается при –1,96<V<1,96, значения, для которых это условие не выполняется, выделены жирным шрифтом цветом. Следовательно, значимая зависимость имеет место между Y и Х5, а также Х1 и Х4.
3.2Регрессионный анализ.
Для построения математической модели выдвинем гипотезу о наличии линейной зависимости между прибылью (иначе Y) и факторами на нее влияющими (Х1, Х2, Х3, Х4, Х5). Следовательно, математическая модель может быть описана уравнением вида:
![]() , (3.1)
, (3.1)
где ![]() - линейно-независимые постоянные коэффициенты.
- линейно-независимые постоянные коэффициенты.
Для их отыскания применим множественный регрессионный анализ. Результаты регрессии сведены в таблицы 3.2 – 3.4.
Таблица 3.2.-Регрессионная статистика.
| Множественный R | 0,609479083 |
| R-квадрат | 0,371464753 |
| Нормированный R-квадрат | 0,161953004 |
| Стандартная ошибка | 24,46839969 |
| Наблюдения | 21 |
Таблица 3.3. –Дисперсионная таблица.
| Степени свободы | SS | MS | F | Значимость F | |
| Регрессия | 5 | 5307,504428 | 1061,500886 | 1,773002013 | 0,179049934 |
| Остаток | 15 | 8980,538753 | 598,7025835 | ||
| Итого | 20 | 14288,04318 |
Таблица 3.4 – Коэффициенты регрессии.
|
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| B0 | 38,950215 | 35,7610264 | 1,0891805 | 0,29326 | -37,272 | 115,173 | -37,2726 | 115,173 |
| B1 | 4,5371110 | 8,42440677 | 0,5385674 | 0,59808 | -13,419 | 22,4933 | -13,4190 | 22,4933 |
| B2 | 1,8305781 | 8,73999438 | 0,2094484 | 0,83691 | -16,798 | 20,4594 | -16,7982 | 20,4594 |
| B3 | 23,645979 | 27,4788285 | 0,8605162 | 0,40304 | -34,923 | 82,2157 | -34,9237 | 82,2157 |
| B4 | -0,526248 | 0,28793074 | -1,827690 | 0,08755 | -1,1399 | 0,08746 | -1,13995 | 0,08746 |
| B5 | -10,780037 | 4,95649626 | -2,174931 | 0,04604 | -21,344 | -0,21550 | -21,3445 | -0,21550 |
Таким образом, уравнение, описывающее математическую модель, приобретает вид:
Y=4,53711108952303*X1+1,830578196*X2+23,64597929*X3- 0,526248308*X5-10,78003746*X5+38,95021506. (3.2)
Для оценки влияния каждого из факторов на результирующую математическую модель применим метод множественной линейной регрессии к нормированным значениям переменных ![]() , результаты пересчета коэффициентов приведены в таблице 3.5.
, результаты пересчета коэффициентов приведены в таблице 3.5.
Таблица 3.5. – Оценка влияния факторов.
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение | 38,95021506 | 35,76102644 | 1,089180567 |
| Переменная X 1 | 3,828821785 | 7,109270974 | 0,538567428 |
| Переменная X 2 | 1,348658856 | 6,439097143 | 0,209448441 |
| Переменная X 3 | 5,367118917 | 6,237091662 | 0,86051628 |
| Переменная X 4 | -12,43702261 | 6,804774783 | -1,827690556 |
| Переменная X 5 | -12,96551745 | 5,961346518 | -2,174931018 |
Коэффициенты в таблице 3.5 показывают степень влияния каждой из переменных на результат (Y). Чем больше коэффициент, тем сильнее прямая зависимость (отрицательные коэффициенты показывают обратную зависимость).
F-критерий из таблицы 3.3 показывает степень адекватности полученной математической модели.
ВЫВОДЫ
В результате проведенной работы был произведен статистический анализ исходных данных, полученных при исследовании основных показателей деятельности предприятия, с целью выявления доминирующих факторов влияющих на прибыль и построена адекватная математическая модель и спрогнозирована прибыль на последующие периоды.
В процессе выполнения работы изучили и научились применять на практике следующие методы математической статистики:
ü линейный регрессионный анализ,
ü множественный регрессионный анализ,
ü корреляционный анализ,
ü проверка стационарности и независимости выборок,
ü выявление тренда,
ü критерий ![]() .
.
Перечень ссылок
1. Бендод Дж., Пирсол А. Прикладной анализ случайных данных: Пер. с англ. – М.: Мир, 1989.
2. Математическая статистика. Под ред. А. М. Длина, М.: Высшая школа, 1975.
3. Л.Н.Большев, Н.В.Смирнов. Таблицы математической статистики.-М.: Наука, 1983.
4. Н.Дрейпер, Г.Смит. Прикладной регрессионный анализ. Пер. с англ.- М.: Статистика, 1973.
Вероятностные ряды ID
| Месяц | 1994 | 1996 | 1997 | 1998 |
| Январь | 1500000 | 1650000 | 1400000 | 1700000 |
| Февраль | 900000 | 850000 | 890000 | 1200000 |
| Март | 700000 | 600000 | 550000 | 459000 |
| Апрель | 300000 | 125000 | 250000 | 221000 |
| Май | 400000 | 300000 | 100000 | 1000 |
| Июнь | 250000 | 450000 | 150000 | 250000 |
| Июль | 200000 | 600000 | 132000 | 325000 |
| Август | 150000 | 750000 | 142000 | 354000 |
| Сентябрь | 300000 | 300000 | 254000 | 150000 |
| Октябрь | 250000 | 259000 | 350000 | 100000 |
| Ноябрь | 400000 | 453000 | 450000 | 259000 |
| Декабрь | 2000000 | 1700000 | 1000000 | 1900000 |
Регрессионный анализ ID
|
| Прибыль | Коэффициент качества продукции | Доля в общем объеме продаж | Розничная цена | Коэффициент издержек на 1 продукции | Удовлетворение условий розничных торговцев |
| № | Y, % | X1 | X2 | X3 | X4 | X5 |
| 1 | 1,99 | 1,22 | 1,24 | 1,3 | 35,19 | 2,08 |
| 2 | 12,21 | 1,45 | 1,54 | 1,04 | 80 | 1,09 |
| 3 | 23,07 | 1,9 | 1,31 | 1 | 23,31 | 2,28 |
| 4 | 24,14 | 2,53 | 1,36 | 1,64 | 80 | 1,44 |
| 5 | 35,05 | 3,41 | 2,65 | 1,19 | 80 | 1,75 |
| 6 | 36,87 | 1,96 | 1,63 | 1,26 | 68,84 | 1,54 |
| 7 | 4,7 | 2,71 | 1,66 | 1,28 | 80 | 0,47 |
| 8 | 58,45 | 1,76 | 1,4 | 1,42 | 30,32 | 2,51 |
| 9 | 59,55 | 2,09 | 2,61 | 1,65 | 80 | 2,81 |
| 10 | 61,42 | 1,1 | 2,42 | 1,24 | 32,94 | 0,59 |
| 11 | 61,51 | 3,62 | 3,5 | 1,09 | 28,56 | 0,64 |
| 12 | 61,95 | 3,53 | 1,29 | 1,29 | 78,75 | 1,73 |
| 13 | 71,24 | 2,09 | 2,44 | 1,65 | 38,63 | 1,83 |
| 14 | 71,45 | 1,54 | 2,6 | 1,19 | 48,67 | 0,76 |
| 15 | 81,88 | 2,41 | 2,11 | 1,64 | 40,83 | 0,14 |
| 16 | 10,08 | 3,64 | 2,06 | 1,46 | 80 | 3,53 |
| 17 | 10,25 | 2,61 | 1,85 | 1,59 | 80 | 2,13 |
| 18 | 10,81 | 2,62 | 2,28 | 1,57 | 80 | 3,86 |
| 19 | 11,09 | 3,29 | 4,07 | 1,78 | 80 | 1,28 |
| 20 | 12,64 | 1,24 | 1,84 | 1,38 | 31,2 | 4,25 |
| 21 | 12,92 | 1,37 | 1,9 | 1,55 | 29,49 | 3,98 |
|
| Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу | Среднее по столбцу |
| M(X) | 34,91761905 | 2,29 | 2,083809524 | 1,390952381 | 57,46333333 | 1,937619048 |
|
| Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу |
| D(X) | 714,402159 | 0,71215 | 0,542784762 | 0,051519048 | 558,5363233 | 1,446569048 |
| S2 | 26,72830258 | 0,843889803 | 0,736739277 | 0,226978077 | 23,63337308 | 1,202733989 |
| Ковариционная матрица | ||||||
|
| Y | X1 | X2 | X3 | X4 | X5 |
| Y | 680,3830086 | 0,214214286 | 4,18483288 | -0,066102494 | -189,5780492 | -13,53461519 |
| X1 | 0,214214286 | 0,678238095 | 0,226847619 | 0,026757143 | 10,04216667 | -0,127428571 |
| X2 | 4,18483288 | 0,226847619 | 0,516937868 | 0,039539229 | 1,061201587 | -0,170019501 |
| X3 | -0,066102494 | 0,026757143 | 0,039539229 | 0,04906576 | 1,29965873 | 0,068287982 |
| X4 | -189,5780492 | 10,04216667 | 1,061201587 | 1,29965873 | 531,9393556 | -1,12405873 |
| X5 | -13,53461519 | -0,127428571 | -0,170019501 | 0,068287982 | -1,12405873 | 1,377684807 |
| Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего | Отклонение от среднего |
| Y | X1 | X2 | X3 | X4 | X5 |
| -32,92761905 | -1,07 | -0,843809524 | -0,090952381 | -22,27333333 | 0,142380952 |
| -22,70761905 | -0,84 | -0,543809524 | -0,350952381 | 22,53666667 | -0,847619048 |
| -11,84761905 | -0,39 | -0,773809524 | -0,390952381 | -34,15333333 | 0,342380952 |
| -10,77761905 | 0,24 | -0,723809524 | 0,249047619 | 22,53666667 | -0,497619048 |
| 0,132380952 | 1,12 | 0,566190476 | -0,200952381 | 22,53666667 | -0,187619048 |
| 1,952380952 | -0,33 | -0,453809524 | -0,130952381 | 11,37666667 | -0,397619048 |
| -30,21761905 | 0,42 | -0,423809524 | -0,110952381 | 22,53666667 | -1,467619048 |
| 23,53238095 | -0,53 | -0,683809524 | 0,029047619 | -27,14333333 | 0,572380952 |
| 24,63238095 | -0,2 | 0,526190476 | 0,259047619 | 22,53666667 | 0,872380952 |
| 26,50238095 | -1,19 | 0,336190476 | -0,150952381 | -24,52333333 | -1,347619048 |
| 26,59238095 | 1,33 | 1,416190476 | -0,300952381 | -28,90333333 | -1,297619048 |
| 27,03238095 | 1,24 | -0,793809524 | -0,100952381 | 21,28666667 | -0,207619048 |
| 36,32238095 | -0,2 | 0,356190476 | 0,259047619 | -18,83333333 | -0,107619048 |
| 36,53238095 | -0,75 | 0,516190476 | -0,200952381 | -8,793333333 | -1,177619048 |
| 46,96238095 | 0,12 | 0,026190476 | 0,249047619 | -16,63333333 | -1,797619048 |
| -24,83761905 | 1,35 | -0,023809524 | 0,069047619 | 22,53666667 | 1,592380952 |
| -24,66761905 | 0,32 | -0,233809524 | 0,199047619 | 22,53666667 | 0,192380952 |
| -24,10761905 | 0,33 | 0,196190476 | 0,179047619 | 22,53666667 | 1,922380952 |
| -23,82761905 | 1 | 1,986190476 | 0,389047619 | 22,53666667 | -0,657619048 |
| -22,27761905 | -1,05 | -0,243809524 | -0,010952381 | -26,26333333 | 2,312380952 |
| -21,99761905 | -0,92 | -0,183809524 | 0,159047619 | -27,97333333 | 2,042380952 |
| Погрешность | Погрешность | Погрешность | Погрешность | Погрешность | Погрешность |
| -2,84217E-14 | 0 | -9,10383E-15 | 0 | 4,26326E-14 | -5,32907E-15 |
| Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего | Квадраты отклонений от среднего |
| Y | X1 | X2 | X3 | X4 | X5 |
| 1084,228096 | 1,1449 | 0,712014512 | 0,008272336 | 496,1013778 | 0,020272336 |
| 515,6359628 | 0,7056 | 0,295728798 | 0,123167574 | 507,9013444 | 0,71845805 |
| 140,3660771 | 0,1521 | 0,598781179 | 0,152843764 | 1166,450178 | 0,117224717 |
| 116,1570723 | 0,0576 | 0,523900227 | 0,062024717 | 507,9013444 | 0,247624717 |
| 0,017524717 | 1,2544 | 0,320571655 | 0,040381859 | 507,9013444 | 0,035200907 |
| 3,811791383 | 0,1089 | 0,205943084 | 0,017148526 | 129,4285444 | 0,158100907 |
| 913,1045009 | 0,1764 | 0,179614512 | 0,012310431 | 507,9013444 | 2,153905669 |
| 553,7729533 | 0,2809 | 0,467595465 | 0,000843764 | 736,7605444 | 0,327619955 |
| 606,7541914 | 0,04 | 0,276876417 | 0,067105669 | 507,9013444 | 0,761048526 |
| 702,3761961 | 1,4161 | 0,113024036 | 0,022786621 | 601,3938778 | 1,816077098 |
| 707,1547247 | 1,7689 | 2,005595465 | 0,090572336 | 835,4026778 | 1,683815193 |
| 730,74962 | 1,5376 | 0,63013356 | 0,010191383 | 453,1221778 | 0,043105669 |
| 1319,315358 | 0,04 | 0,126871655 | 0,067105669 | 354,6944444 | 0,011581859 |
| 1334,614858 | 0,5625 | 0,266452608 | 0,040381859 | 77,32271111 | 1,386786621 |
| 2205,465225 | 0,0144 | 0,000685941 | 0,062024717 | 276,6677778 | 3,23143424 |
| 616,90732 | 1,8225 | 0,000566893 | 0,004767574 | 507,9013444 | 2,535677098 |
| 608,4914295 | 0,1024 | 0,054666893 | 0,039619955 | 507,9013444 | 0,037010431 |
| 581,1772961 | 0,1089 | 0,038490703 | 0,03205805 | 507,9013444 | 3,695548526 |
| 567,7554295 | 1 | 3,944952608 | 0,15135805 | 507,9013444 | 0,432462812 |
| 496,2923104 | 1,1025 | 0,059443084 | 0,000119955 | 689,7626778 | 5,347105669 |
| 483,8952438 | 0,8464 | 0,033785941 | 0,025296145 | 782,5073778 | 4,171319955 |
| Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу | Дисперсия по столбцу |
| 714,402159 | 0,71215 | 0,542784762 | 0,051519048 | 558,5363233 | 1,446569048 |
| Кореляционная матрица | |||||||
| Y | X1 | X2 | X3 | X4 | X5 | ||
| Y | R | 0,952380952 | 0,009497107 | 0,212516628 | -0,010895886 | -0,300117251 | -0,421022155 |
|
| V | 8,30379958 | 0,042473629 | 0,965111718 | -0,048729813 | -1,384789996 | -2,007692777 |
| X1 | R | 0,009497107 | 0,952380952 | 0,364867065 | 0,139691534 | 0,503519129 | -0,125548489 |
|
| V | 0,042473629 | 8,30379958 | 1,710542787 | 0,628831315 | 2,477605293 | -0,564448173 |
| X2 | R | 0,212516628 | 0,364867065 | 0,952380952 | 0,236445177 | 0,060947845 | -0,191873647 |
|
| V | 0,965111718 | 1,710542787 | 8,30379958 | 1,077808965 | 0,272905301 | -0,868854214 |
| X3 | R | -0,010895886 | 0,139691534 | 0,236445177 | 0,952380952 | 0,242281194 | 0,250144398 |
|
| V | -0,048729813 | 0,628831315 | 1,077808965 | 8,30379958 | 1,105494772 | 1,142929664 |
| X4 | R | -0,300117251 | 0,503519129 | 0,060947845 | 0,242281194 | 0,952380952 | -0,039545194 |
|
| V | -1,384789996 | 2,477605293 | 0,272905301 | 1,105494772 | 8,30379958 | -0,176943758 |
| X5 | R | -0,421022155 | -0,125548489 | -0,191873647 | 0,250144398 | -0,039545194 | 0,952380952 |
| V | -2,007692777 | -0,564448173 | -0,868854214 | 1,142929664 | -0,176943758 | 8,30379958 | |
| Область принятия гипотезы | -1,96 | 1,96 | |||||
Регрессия
| ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
| Множественный R | 0,009971962 |
| R-квадрат | 9,944E-05 |
| Нормированный R-квадрат | -0,052526905 |
| Стандартная ошибка | 27,42129635 |
| Наблюдения | 21 |
| Дисперсионный анализ | ||||||||
|
| df | SS | MS | F | Значимость F | |||
| Регрессия | 1 | 1,42080336 | 1,42080336 | 0,001889548 | 0,965781312 | |||
| Остаток | 19 | 14286,62238 | 751,9274936 | |||||
| Итого | 20 | 14288,04318 | ||||||
|
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | 34,19434691 | 17,68210005 | 1,933839692 | 0,068170144 | -2,814725323 | 71,20341915 | -2,814725323 | 71,20341915 |
| Переменная X 1 | 0,31583936 | 7,265863675 | 0,043468936 | 0,965781312 | -14,89179281 | 15,52347153 | -14,89179281 | 15,52347153 |
| ВЫВОД ОСТАТКА | |||
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 1 | 34,57967093 | -32,58967093 | -1,280111564 |
| 2 | 34,65231399 | -22,44231399 | -0,881526718 |
| 3 | 34,7944417 | -11,7244417 | -0,460532217 |
| 4 | 34,99342049 | -10,85342049 | -0,42631879 |
| 6 | 34,81339206 | 2,056607941 | 0,080782884 |
| 7 | 35,05027158 | -30,35027158 | -1,192148693 |
| 8 | 34,75022419 | 23,69977581 | 0,930919405 |
| 9 | 34,85445118 | 24,69554882 | 0,970033042 |
| 10 | 34,54177021 | 26,87822979 | 1,055768033 |
| 11 | 35,3376854 | 26,1723146 | 1,028039916 |
| 12 | 35,30925985 | 26,64074015 | 1,046439518 |
| 14 | 34,68073953 | 36,76926047 | 1,444284467 |
| 15 | 34,95551977 | 46,92448023 | 1,843178162 |
| 16 | 35,34400218 | -25,26400218 | -0,992361703 |
| 17 | 35,01868764 | -24,76868764 | -0,972905911 |
| 18 | 35,02184604 | -24,21184604 | -0,951033355 |
| 19 | 35,23345841 | -24,14345841 | -0,948347112 |
| 20 | 34,58598772 | -21,94598772 | -0,862031185 |
| 21 | 34,62704684 | -21,70704684 | -0,852645666 |
Анализ У
| Прибыль | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| Y, % | 7 | ||||
| 1,99 | - | 0 | 8 | 12,68132103 | 0,221751084 |
| 12,21 | - | 5 | 2 | 23,37264207 | 0,285525351 |
| 23,07 | - | 7 | 1 | 34,0639631 | 0,313282748 |
| 24,14 | + | 7 | 2 | 44,75528414 | 0,2929147 |
| 35,05 | + | 7 | 0 | 55,44660517 | 0,233377369 |
| 36,87 | + | 7 | 5 | 66,1379262 | 0,158448887 |
| 4,7 | - | 0 | 2 | 76,82924724 | 0,091671119 |
| 58,45 | + | 6 | |||
| 59,55 | + | 6 | |||
| 61,42 | + | 6 | |||
| 61,51 | + | 6 | |||
| 61,95 | + | 6 | |||
| 71,24 | + | 6 | |||
| 71,45 | + | 6 | |||
| 81,88 | + | 6 | |||
| 10,08 | - | 0 | |||
| 10,25 | - | 0 | |||
| 10,81 | - | 0 | |||
| 11,09 | - | 0 | |||
| 12,64 | - | 0 | |||
| 12,92 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 34,91761905 | 22,75082838 | 47,08440971 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 714,402159 | 439,0531267 | 1564,38429 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 26,72830258 | Критерий серий | 4,6762E-100 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 24,14 | 5 | 5 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12,6 | |||
| 79,89 | |||||
| Вариация | Критерий инверсий | ||||
| 77% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 81 | 125 | ||
| 0,370221636 | тренд отсутствует | ||||
| Эксцес | |||||
| -1,551701276 | |||||
Анализ X1
| Коэффициент качества продукции | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X1 | 7 | ||||
| 1,22 | - | 1 | 4 | 1,437555921 | 5,960349765 |
| 1,45 | - | 3 | 3 | 1,775111843 | 8,241512255 |
| 1,9 | - | 5 | 4 | 2,112667764 | 9,71079877 |
| 2,53 | + | 9 | 1 | 2,450223685 | 9,750252967 |
| 3,41 | + | 13 | 4 | 2,787779606 | 8,342374753 |
| 1,96 | - | 5 | 0 | 3,125335528 | 6,082419779 |
| 2,71 | + | 10 | 2 | 3,462891449 | 3,778991954 |
| 1,76 | - | 4 | |||
| 2,09 | + | 4 | |||
| 1,1 | - | 0 | |||
| 3,62 | + | 9 | |||
| 3,53 | + | 8 | |||
| 2,09 | + | 3 | |||
| 1,54 | - | 2 | |||
| 2,41 | + | 2 | |||
| 3,64 | + | 5 | |||
| 2,61 | + | 2 | |||
| 2,62 | + | 2 | |||
| 3,29 | + | 2 | |||
| 1,24 | - | 0 | |||
| 1,37 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 2,29 | 1,905859236 | 2,674140764 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0,71215 | 0,437669008 | 1,559452555 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0,843889803 | Критерий серий | 0,000980756 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 2,09 | 5 | 11 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12,6 | |||
| 2,54 | |||||
| Вариация | Критерий инверсий | ||||
| 37% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 89 | 125 | ||
| 0,290734565 | тренд отсутствует | ||||
| Эксцес | |||||
| -1,161500717 | |||||
Анализ Х2
| Доля в общем объеме продаж | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X2 | 9 | ||||
| 1,24 | - | 0 | 5 | 1,534695711 | 8,613638207 |
| 1,54 | - | 4 | 3 | 1,829391421 | 10,71322271 |
| 1,31 | - | 1 | 5 | 2,124087132 | 11,35446101 |
| 1,36 | - | 1 | 1 | 2,418782843 | 10,25476697 |
| 2,65 | + | 14 | 5 | 2,713478553 | 7,892197623 |
| 1,63 | - | 2 | 0 | 3,008174264 | 5,175865594 |
| 1,66 | - | 2 | 0 | 3,302869975 | 2,892550245 |
| 1,4 | - | 1 | 1 | 3,597565686 | 1,377500344 |
| 2,61 | + | 10 | 1 | 3,892261396 | 0,559004628 |
| 2,42 | + | 7 | |||
| 3,5 | + | 9 | |||
| 1,29 | - | 9 | |||
| 2,44 | + | 6 | |||
| 2,6 | + | 6 | |||
| 2,11 | + | 4 | |||
| 2,06 | + | 3 | |||
| 1,85 | - | 1 | |||
| 2,28 | + | 2 | |||
| 4,07 | + | 2 | |||
| 1,84 | - | 0 | |||
| 1,9 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 2,083809524 | 1,748443949 | 2,419175098 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0,542784762 | 0,333581504 | 1,188579771 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0,736739277 | Критерий серий | 0,000201468 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1,9 | 5 | 10 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12,6 | |||
| 2,83 | |||||
| Вариация | Критерий инверсий | ||||
| 35% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 84 | 125 | ||
| 1,189037981 | тренд отсутствует | ||||
| Эксцес | |||||
| 1,48713312 | |||||
Анализ Х3
| Розничная цена | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X3 | 8 | ||||
| 1,3 | - | 9 | 3 | 1,090791231 | 15,39563075 |
| 1,04 | - | 1 | 0 | 1,181582462 | 24,12028441 |
| 1 | - | 0 | 4 | 1,272373693 | 32,20180718 |
| 1,64 | + | 13 | 3 | 1,363164924 | 36,63455739 |
| 1,19 | - | 1 | 2 | 1,453956155 | 35,51522214 |
| 1,26 | - | 3 | 1 | 1,544747386 | 29,33938492 |
| 1,28 | - | 3 | 3 | 1,635538617 | 20,65381855 |
| 1,42 | + | 5 | 4 | 1,726329848 | 12,38975141 |
| 1,65 | + | 10 | |||
| 1,24 | - | 2 | |||
| 1,09 | - | 0 | |||
| 1,29 | - | 1 | |||
| 1,65 | + | 7 | |||
| 1,19 | - | 0 | |||
| 1,64 | + | 5 | |||
| 1,46 | + | 1 | |||
| 1,59 | + | 3 | |||
| 1,57 | + | 2 | |||
| 1,78 | + | 2 | |||
| 1,38 | + | 0 | |||
| 1,55 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 1,390952381 | 1,287631388 | 1,494273374 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 0,051519048 | 0,031662277 | 0,112815433 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 0,226978077 | Критерий серий | 3,27644E-33 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1,38 | 5 | 8 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12,6 | |||
| 0,78 | |||||
| Вариация | Критерий инверсий | ||||
| 16% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 68 | 125 | ||
| -0,060264426 | тренд отсутствует | ||||
| Эксцес | |||||
| -1,116579819 | |||||
Анализ Х4
| Коэффициент издержек на 1 продукции | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X4 | 5 | ||||
| 35,19 | - | 6 | 5 | 32,76334923 | 0,205311711 |
| 80 | + | 11 | 4 | 42,21669847 | 0,287891016 |
| 23,31 | - | 0 | 1 | 51,6700477 | 0,343997578 |
| 80 | + | 10 | 0 | 61,12339693 | 0,350264029 |
| 80 | + | 10 | 1 | 70,57674617 | 0,30391251 |
| 68,84 | + | 8 | |||
| 80 | + | 9 | |||
| 30,32 | - | 3 | |||
| 80 | + | 8 | |||
| 32,94 | - | 3 | |||
| 28,56 | - | 0 | |||
| 78,75 | + | 5 | |||
| 38,63 | - | 2 | |||
| 48,67 | - | 3 | |||
| 40,83 | - | 2 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 80 | + | 2 | |||
| 31,2 | - | 1 | |||
| 29,49 | - | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 57,46333333 | 46,70536237 | 68,22130429 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 558,5363233 | 343,2620073 | 1223,072241 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 23,63337308 | Критерий серий | 7,37999E-32 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 68,84 | 5 | 11 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12,6 | |||
| 56,69 | |||||
| Вариация | Критерий инверсий | ||||
| 41% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 89 | 125 | ||
| -0,199328538 | тренд отсутствует | ||||
| Эксцес | |||||
| -1,982514776 | |||||
Анализ Х5
| Удовлетворение условий розничных торговцев | Критерий серий | Критерий инверсий | Расчетная частота | Интервалы группировки | Теоретическая частота |
| X5 | 8 | ||||
| 2,08 | + | 12 | 3 | 0,621093595 | 3,826307965 |
| 1,09 | - | 5 | 3 | 1,102187191 | 5,47254967 |
| 2,28 | + | 12 | 3 | 1,583280786 | 6,669793454 |
| 1,44 | - | 6 | 3 | 2,064374382 | 6,927043919 |
| 1,75 | + | 8 | 4 | 2,545467977 | 6,130506823 |
| 1,54 | - | 6 | 1 | 3,026561573 | 4,623359901 |
| 0,47 | - | 1 | 0 | 3,507655168 | 2,971200139 |
| 2,51 | + | 8 | 3 | 3,988748764 | 1,627117793 |
| 2,81 | + | 8 | |||
| 0,59 | - | 1 | |||
| 0,64 | - | 1 | |||
| 1,73 | - | 3 | |||
| 1,83 | + | 3 | |||
| 0,76 | - | 1 | |||
| 0,14 | - | 0 | |||
| 3,53 | + | 2 | |||
| 2,13 | + | 1 | |||
| 3,86 | + | 1 | |||
| 1,28 | - | 0 | |||
| 4,25 | + | 1 | |||
| 3,98 | + | 0 | |||
| Среднее по столбцу | Доверительный интервал | ||||
| 1,937619048 | 1,390131506 | 2,485106589 | |||
| Дисперсия по столбцу | Доверительный интервал | ||||
| 1,446569048 | 0,889023998 | 3,167669447 | |||
| Cреднее квадратичное отклонение | Хи-квадрат критерий | ||||
| 1,202733989 | Критерий серий | 0,066231679 | |||
| Медиана | мин. | рассчетное | макс. | ||
| 1,75 | 5 | 13 | 15 | Табличное значение | |
| Размах | тренд отсутствует | 12,6 | |||
| 4,11 | |||||
| Вариация | Критерий инверсий | ||||
| 62% | мин. | рассчетное | макс. | ||
| Ассиметрия | 64 | 80 | 125 | ||
| 0,527141402 | тренд отсутствует | ||||
| Эксцес | |||||
| -0,580795634 | |||||
Похожие работы
... несколько уравнений, а в каждом уравнении - несколько переменных. Задача оценивания параметров такой разветвленной модели решается с помощью сложных и причудливых методов. Однако все они имеют одну и ту же теоретическую основу. Поэтому для получения начального представления о содержании эконометрических методов мы ограничимся в последующих параграфах рассмотрением простой линейной регрессии. ...
... ПО “Уралмаш”, “АвтоВАЗ”, МИИТ, Казахского политехнического института, Донецкого государственного университета и многих других. Затем Институт в качестве Лаборатории эконометрических исследований разрабатывал эконометрические методы анализа нечисловых данных, а также процедуры расчета и прогнозирования индекса инфляции и валового внутреннего продукта. Институт высоких статистических технологий и ...
... на задний план традиционными постановками. Несколько лет назад при описании современного этапа развития статистических методов нами были выделены [29] пять актуальных направлений, в которых развивается современная прикладная статистика, т.е. пять "точек роста": непараметрика, робастность, бутстреп, интервальная статистика, статистика объектов нечисловой природы. Обсудим их. 5. ...
... и боятся бедности и как следствие воспитывают своих детей в такой же привычке к труду и благосостоянию, а удача доставляет удовлетворение их родительским чувствам и самолюбию. Принадлежит первое в истории экономической мысли достаточно глубокое теоретическое обоснование положений о капитале. Считал, “что деньги сами по себе представляют собой бесплодное богатство, которое ничего не производит”. ...
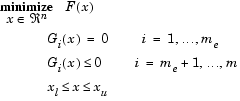
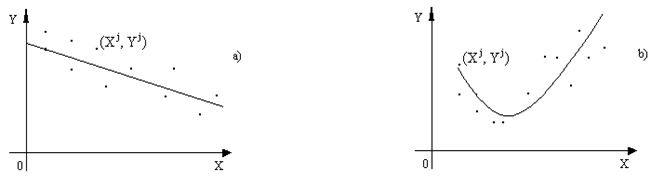

0 комментариев