Момент імпульсу частинки

12 Момент імпульсу частинки.

Аналіз поведінки систем показує, що крім енергії та імпульсу існує ще одна механічна величина, з якою також пов’язаний закон збереження – це момент імпульсу . що це за величина і які її властивості? |[pic] |[pic] | |Рис. 1 |Рис. 2 |

Візьмемо спочатку одну частинку. Нехай [pic][pic] – радіус-вектор, який характеризує її положення відносно деякої точки [pic] вибраної системи відліку, а [pic] – її імпульс в цій системі (рис. 1). Момент імпульсу [pic] матеріальної точки відносно деякої точки [pic] називається векторний добуток радіус-вектора [pic] на її імпульс [pic]:

[pic]. (17)

Модуль цієї величини, що дорівнює [pic], можна представити у вигляді добутку плеча [pic] імпульсу на модуль вектора [pic]:

[pic].

Частинка володіє моментом імпульсу незалежно від форми траєкторії, по якій вона рухається. Розглянемо два випадки. |[pic] | |Рис. 3 |

Частинка рухається вздовж прямолінійної траєкторії (рис. 3). Модуль моменту імпульсу [pic] може змінюватися тільки за рахунок зміни модуля швидкості. |[pic] | |Рис. 4 |

Частинка рухається по колу радіуса [pic] (рис. 4). Модуль моменту імпульсу відносно центру кола дорівнює [pic] і так само, як і в попередньому випадку, може змінюватися лише за рахунок зміни модуля швидкості. Не дивлячись на неперервну зміну напряму вектора [pic], напрям вектора [pic] залишається постійним.

Рівняння моментів.

З’ясуємо яка механічна величина відповідає за зміну вектора [pic] в даній системі відліку. Для цього продиференціюємо рівняння (17) по часу:

[pic].

Оскільки точка [pic] є нерухомою, то вектор [pic] дорівнює швидкості [pic] частинки, тобто співпадає за напрямком з вектором [pic], тому:

[pic].

Далі, згідно з другим законом Ньютона, [pic], де [pic] – рівнодійна всіх сил, які прикладені до частинки. Відповідно:

[pic].

Величину, що стоїть в правій частині цього рівняння, називають моментом сили [pic] відносно точки [pic] (рис. 2). Позначивши його буквою [pic], запишемо:

[pic].

Модуль цього вектора дорівнює:

[pic], де [pic] – довжина перпендикулярна, опущеного з точки [pic] на пряму, вздовж якої напрямлений імпульс частинки. Ця відстань називається плечем вектора [pic] відносно точки [pic].

Отже, похідна по часу від моменту імпульсу [pic] частинки відносно деякої точки [pic] вибраної системи відліку дорівнює моменту [pic] рівнодійної сили [pic] відносно тієї ж точки [pic]:

[pic]. (18)

Це рівняння називається рівнянням моментів. Зауважимо, що якщо система відліку є неінерціальною, то момент сили [pic] включає в себе як момент сил взаємодії, так і момент сил інерції (відносно тієї ж точки [pic]).

Із рівняння моментів (18) слідує, що якщо [pic], то [pic]. Іншими словами, якщо відносно деякої точки [pic] вибраної системи відліку момент усіх сил, що діють на частинку, дорівнює нулю протягом певного проміжку часу, який нас цікавить, то відносно цієї точки момент імпульсу частинки залишається постійним протягом цього часу. Рівняння моментів (18) дозволяє отримати відповідь на два питання: знайти момент сили [pic] відносно довільної точки [pic] в будь-який проміжок часу [pic], якщо відома залежність від часу моменту імпульсу [pic] частинки відносно тієї ж точки; визначити приріст моменту імпульсу частинки відносно точки [pic] за довільний проміжок часу, якщо відома залежність від часу моменту сили [pic], що діє на цю частинку (відносно тієї ж точки [pic]).

Вирішення першого питання зводиться до знаходження похідної по часу від моменту імпульсу, тобто [pic], яка і дорівнює шуканому моменту сили [pic].

Вирішення другого питання зводиться до інтегрування рівняння (18). Помноживши обидві частини цього рівняння на [pic], отримаємо [pic] – вираз, який визначає елементарний приріст вектора [pic]. Проінтегрувавши цей вираз по часу, знайдемо приріст вектора [pic] за скінчений проміжок часу [pic]:

[pic].

Величину, яка стоїть в правій частині цього рівняння, називають імпульсом моменту сили. Таким чином, приріст моменту імпульсу частинки за довільний проміжок часу дорівнює імпульсу моменту сили за той же час.

Момент імпульсу і момент сили відносно осі.

Візьмемо в деякій системі відліку довільну нерухому вісь [pic]. Нехай відносно деякої точки [pic] на осі [pic] момент імпульсу частинки [pic] дорівнює [pic], а момент сили, що діє на частинку, [pic].

Моментом імпульсу відносно осі [pic] називають проекцію на цю вісь вектора [pic], визначеного відносно довільної точки [pic] даної осі (рис. 5). |[pic] | |Рис. 5 |

Аналогічно вводиться і поняття моменту сили відносно осі. Їх позначають відповідно [pic] і [pic]. Далі ми побачимо, що [pic] та [pic] не залежать від вибору точки [pic] на осі [pic].

З’ясуємо властивості цих величин. Спроектувавши (18) на вісь [pic], отримаємо:

[pic], тобто похідна по часу від моменту імпульсу частинки відносно осі [pic] дорівнює моменту сили відносно цієї осі. Якщо [pic], то [pic]. Іншими словами, якщо момент сили відносно деякої нерухомої осі [pic] дорівнює нулю, то момент імпульсу частинки відносно цієї осі залишається постійним. При цьому сам вектор [pic] може і змінюватися.

Знайдемо тепер аналітичний вираз для [pic] і [pic]. Неважко побачити, що ця задача зводиться до знаходження проекцій нам вісь [pic] векторних добутків [pic] і [pic].

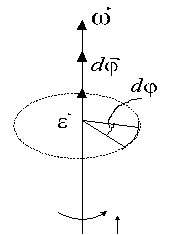
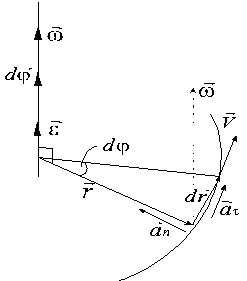
Скористуємось циліндричною системою координат [pic], [pic], [pic], пов’язавши з частинкою [pic] (рис. 6) орти [pic], [pic], [pic], які напрямлені в бік зростання відповідних координат. |[pic] | |Рис. 6 |

В цій системі координат радіус-вектор [pic] та імпульс [pic] частинки записують так:

[pic], [pic], де [pic], [pic], [pic] – проекції вектора [pic] на відповідні орти. З векторної алгебри відомо, що векторний добуток [pic] можна представити визначником:

[pic].

Звідси одразу видно, що моменти імпульсу частинки відносно осі [pic]:

[pic], де [pic] – відстань частинки від осі [pic]. Перетворимо цей вираз до виду, який більш зручніший для практичного застосування. Маючи на увазі, що [pic], отримаємо:

[pic], де [pic] – проекція кутової швидкості [pic], з якою обертається радіус- вектор частинки.

Запишемо момент сили відносно осі [pic]:

[pic], де [pic] – проекція вектора сили [pic] на орт [pic].

Звернемо увагу, що проекція [pic] і [pic] дійсно не залежать від вибору точки [pic] на осі [pic], відносно якої визначені вектори [pic] і [pic]. Крім того, [pic] і [pic] – величини алгебраїчні, їх знаки відповідають знакам проекції [pic] і [pic].

Закон збереження моменту імпульсу.

Виберемо довільну систему частинок. Введемо поняття моменту імпульсу даної системи як векторну суму моментів імпульсів її окремих частин:

[pic], (19) де всі вектори визначені відносно однієї і тієї ж точки [pic] заданої системи відліку. Зауважимо, що момент імпульсу системи – величина адитивна: момент імпульсу системи дорівнює сумі моментів імпульсів її окремих частин незалежно від того, взаємодіють вони між собою, чи ні.

З’ясуємо, яка величина визнає зміну моменту імпульсу системи. Для цього продиференціюємо (19) по часу:

[pic].

А похідна [pic] дорівнює моменту всіх сил, що діють на [pic]-ту частинку. Представимо цей момент у вигляді суми моментів внутрішніх і зовнішніх сил, тобто [pic]. Тоді:

[pic].

Тут перша сума – це сумарний момент всіх внутрішніх сил відносно точки [pic], друга сума – сумарний момент всіх зовнішніх сил відносно тієї ж точки [pic].

Покажемо, що сумарний момент всіх внутрішніх сил відносно довільної точки дорівнює нулю. Дійсно, внутрішні сили – це сили взаємодії між частинками даної системи. За третім законом Ньютона, ці сили попарно однакові по модулю, протилежні за напрямком і лежать на одній прямій, тобто мають однакове плече. Тому моменти сил кожної пари взаємодії рівні по модулю і протилежні за напрямком, тобто зрівноважують одна одну, а значить, сумарний момент всіх внутрішніх сил завжди дорівнює нулю.

В результаті останнє рівняння приймає вигляд:

[pic], (20) де [pic] – сумарний момент всіх зовнішніх сил, [pic].

Рівняння (20) стверджує: похідна моменту імпульсу системи по часу дорівнює сумарному моменту всіх зовнішніх сил.

Як і у випадку однієї частинки, з рівняння (20) випливає, що приріст моменту імпульсу системи за скінчений проміжок часу [pic]:

[pic], (21) тобто приріст моменту імпульсу системи дорівнює імпульсу сумарного моменту всіх зовнішніх сил за відповідний проміжок часу. І тут обидва моменти, [pic] і [pic], визначені відносно однієї і тієї ж точки [pic] вибраної системи відліку.

Рівняння (20) і (21) справедливі як в інерційній, так і в неінерційній системах відліку. Тільки в неінерціальній системі відліку потрібно враховувати і дію сил інерції, які відіграють роль зовнішніх сил, тобто за [pic] в цих рівняннях приймати суму [pic], де [pic] – сумарний момент зовнішніх сил взаємодії, [pic] – сумарний момент сил інерції (відносно однієї і тієї ж точки [pic] системи відліку).

Отже, ми прийшли до важливого висновку: згідно з рівнянням (20), момент імпульсу системи може змінюватися під дією лише сумарного моменту всіх зовнішніх сил. Звідси безпосередньо випливає і інший важливий висновок – закон збереження моменту імпульсу: в інерціальній системі відліку момент імпульсу замкнутої системи частинок залишається постійним, тобто не змінюється з часом.

Причому це справедливо для моменту імпульсу, взятого відносно будь- якої точки інерціальної системи відліку.

Таким чином, в інерціальній системі відліку момент імпульсу замкнутої системи частинок:

[pic].

Якісним підтвердженням закону збереження моменту імпульсу може бути дослід з лавкою Жуковського. Демонстраційна лавка, яку запропонував Жуковський, являє собою металевий круг, який обертається з досить малим тертям навколо вертикальної осі. Людина з гантелями в руках сідає на лавку, Момент зовнішніх сил дорівнює нулю (моментом сил тертя можна знехтувати, оскільки сили невеликі; центр тяжіння системи людина – площадка лежить на осі обертання, тобто момент сили тяжіння дорівнює нулю). Лавку приводять в обертання з кутовою швидкістю [pic], коли людина тримає гантелі на витягнутих в сторони руках. Якщо людина піднесе гантелі до грудей, кутова швидкість помірно зросте; при розведенні рук – знову зменшиться. Змінюючи положення гантелей, людина знімає момент інерції.

Закон збереження моменту кількості руху справедливий і для системи твердих тіл. При додаванні рівнянь руху і рівнянь моментів внутрішні сили і моменти внутрішніх сил взаємно знищуються. Тому якщо момент зовнішніх сил, що діють на систему, дорівнює нулю, то загальний момент кількості руху системи залишається незмінним.

Так сила тяжіння, що діє з боку Сонця, не може змінити швидкості обертання Землі навколо осі. Її вплив на швидкість обертання Місяця навколо Землі дуже малий. Тому сума моментів обертання Місяця навколо Землі і обертання Землі навколо осі підкоряються закону збереження моментів. Тертя приливів в земному океані і земній корі, які виникають під дією притягання Місяця, постійно сповільнюють обертання Землі. Дія закону збереження моментів обумовлює збільшення швидкості обертання Місяця навколо Землі. Прискорення руху Місяця на орбіті супроводжується деяким віддаленням його від Землі (біля 1,5 км у століття). Колись, в далекому майбутньому, періоди обертання Місяця навколо Землі і Землі навколо осі стануть однаковими.

Уже з цього прикладу видно, що застосовуючи закон збереження моменту імпульсу до системи тіл, потрібно пам’ятати, що при цьому тіла часто розглядати як матеріальні точки. Тверде тіло може обертатися навколо осі, що проходить через нього і, розглядаючи тіло як точку, ми не враховуємо момент імпульсу.

Із закону збереження моменту імпульсу випливає, що внутрішні сили не можуть змінити момент імпульсу тіла або системи тіл, однак це не означає, що внутрішні сили не можуть змінити момент імпульсу тіла або системи тіл. Однак це не означає, що внутрішні сили не можуть визвати обертання частин всередині системи. Якщо деяка частина системи починає обертатися в одному напрямі, то інша, еквівалентна її частина почне обертатися в протилежному напрямі так, що в цілому для системи закон збереження моменту імпульсу буде виконуватися.

Закон збереження моменту імпульсу відіграє таку ж важливу роль, як і закони збереження енергії та імпульсу. Уже сам по собі від дозволяє зробити в деяких випадках ряд суттєвих висновків про властивості тих чи інших процесів, зовсім не вникаючи в їх детальний розгляд.

Особливий інтерес викликають випадки, коли момент імпульсу [pic] зберігається для незамкнутих систем, у яких, як відомо, імпульс [pic] змінюється з часом. Якщо відносно деякої точки [pic] вибраної системи відліку сумарний момент зовнішніх сил [pic] протягом певного проміжку часу, то момент імпульсу системи відносно точки [pic] зберігається за цей час. У незамкнутих системах, взагалі кажучи, такої точки може і не бути, що слід перш за все з’ясувати для кожного конкретного випадку.

У більш обмеженому випадку в незамкнутих системах може зберігатися не сам момент імпульсу [pic], а його проекція на деяку нерухому вісь [pic]. Це буває тоді, коли проекція сумарного моменту [pic] всіх зовнішніх сил на цю вісь дорівнює нулю. Дійсно, спроектувати рівняння (20) на вісь [pic], сприймаємо:

[pic]. (22) тут [pic] і [pic] – момент імпульсу і сумарний момент зовнішніх сил відносно осі [pic]:

[pic], [pic], де [pic] і [pic] – момент імпульсу і момент зовнішніх сил відносно осі [pic] для [pic]-тої частинки системи.

Із рівняння (22) випливає, що якщо відносно деякої нерухомої в даній системі відліку осі [pic] проекція [pic], то момент імпульсу системи відносно цієї осі зберігається:

[pic].

При цьому сам вектор [pic], визначений відносно довільної точки [pic] на цій осі, може змінюватися. Наприклад, якщо система рухається в однорідному полі тяжіння, то сумарний момент всіх сил тяжіння відносно довільної нерухомої точки [pic] перпендикулярний до вертикалі, а значить, відносно довільної вертикальної осі [pic] і [pic], чого не можна сказати про вектор [pic].

Міркування, які приводять до закону збереження моменту імпульсу, цілком спираються на справедливість законів Ньютона.

Враховуючи значну роль, яку відіграє закон збереження моменту імпульсу в механіці, у фізиці поняття моменту імпульсу поширюють на немеханічні системи (які не підкоряються законам Ньютона) і постулюють закон збереження моменту імпульсу для всіх фізичних процесів.

Такий розширений закон збереження моменту імпульсу уже не є наслідком законів Ньютона, а являє собою самостійний загальний принцип, який є узагальненням дослідних фактів. Поряд із законами збереження енергії та імпульсу закон збереження моменту імпульсу є одним із найважливіших фундаментальних законів природи.

ВИСНОВОК

Кожен із розглянутих законів збереження є унікальним і являється є законом природи. Повна енергія (сума кінетичної і потенціальної енергії) ізольованої системи, в якій діють лише консервативні сили, є величиною сталою, які б механічні зміни не відбувалися при цьому всередині системи. Це твердження називається законом збереження і перетворення механічної енергії. У разі, коли в системі діє і сила тертя, повна механічна енергія не залишається сталою. Дія сил тертя призводить до збільшення внутрішньої енергії. Точні експериментальні дослідження показали, що всі “втрати” механічної енергії дорівнюють збільшення внутрішньої енергії. Це підтверджує, що в природі діє закон збереження і перетворення будь-якого виду енергії.

Енергія ніколи не виникає і не зникає. Вона лише переходить з одного виду в інший.

Закон збереження і перетворення енергій відкритий у 1840 р. Р. Майєром. Незважаючи на те, що вчений здійснив відкриття на основі медико- біологічних досліджень, відкритий ним закон виявився справедливим для усієї природи. Повний імпульс замкнутої системи є величина стала. Це є закон збереження імпульсу. З нього випливає, що внутрішні сили, які діють в системі, не можуть змінити повний імпульс системи, вони можуть зумовити тільки обмін імпульсами окремих тіл системи. Оскільки закон збереження імпульсу є універсальним законом, то він справджується в усіх відомих взаємодіях. Імпульс можуть мати не тільки тіла, а й поля. Прикладом прояву імпульсу електромагнітного поля є тиск світла. При відсутності моменту зовнішніх сил ([pic]). Момент імпульсу тіла залишається незмінним. Це є закон збереження моменту імпульсу. Він охоплює більш широке коло явищ, ніж закон збереження імпульсу. Цей закон дозволяє при вивченні конкретних видів руху повністю виключати із розгляду внутрішні сили, а відповідним вибором осі моментів виключити і ряд зовнішніх сил, моменти, яких відносно даної осі дорівнюють нулю. Тому він широко застосовується не лише в теоретичних дослідженнях, але й в технічних розрахунках.

Закони збереження розглядаються у шкільному курсі фізики в 9 класі. Вводяться поняття енергії, імпульсу та відповідно закони збереження енергії та імпульсу, однак момент імпульсу вивчається лише поверхнево. Оскільки ці закони є дуже важливими і необхідними для кращого опанування матеріалу, то в школі слід детальніше вивчати дану тему.

ЛІТЕРАТУРА

1. Архангельський М.М. Курс физики. Механика. – М.: Просвещение,

1975. – с. 186-190

2. Иродов И.Е. Основные законы механики. – М.: Высшая школа, 1978.

– с. 62-64, 82-91, 100-105, 129-140

3. Савельев И.В. Курс физики. Механика. Молекулярная физика. – М.:

Наука, 1989. – т. 1 – с. 57-60, 89-92

4. Стрелков С.П. Механика. – М.: Наука, 1975. – с. 95-96