Навигация
Шумовые характеристики волоконно-оптического контура
2.2. Шумовые характеристики волоконно-оптического контура
В оптической гироскопии для намотки чувствительного контура используют три вида волокна: многомодовое, одномодовое и одномодовое с устойчивой поляризацией. Длина периметра контура определяется исходя из двух предпосылок. С одной стороны, увеличение длины контура повышает точность системы в целом, так как величина невзаимного фазового сдвига пропорциональна длине волокна, с другой стороны для более длинного контура в большей степени на работу системы оказывают влияние параметры затухания и нерегулярности волокна. Системы, где требуется высокая чувствительность к низким скоростям вращения подразумевают выбор оптимальной длины контура с учетом всех возможных факторов влияющих на точностные характеристики системы. Обычно используются волокна длиной от 200 до 1500 м.
Диаметр катушки выбирается по критерию минимизации потерь в волокне на изгибах и с учетом габаритных размеров устройства. Типовое значение от 6 до 40 см.
В зависимости от числа распространяющихся на рабочей частоте волн (мод) могут использоваться одно- и многомодовые световоды.
Для характеристик световода важное значение имеет профиль показателя преломления в поперечном сечении. Используя возможности неоднородных световодов в широких пределах изменять свои характеристики в зависимости от закона изменения диэлектрической проницаемости по поперечному сечению, можно для каждого конкретного применения подобрать световод с наилучшим соответствием его характеристик решению задачи.
Важной характеристикой световода является числовая апертура NA, представляющая собой синус максимального угла падения лучей на торец световода, при котором в световоде луч на границу «сердцевина-оболочка» падает под критическим углом. От значения NA зависят эффективность ввода излучения светодиода в световод, потери на микроизгибах, дисперсия импульсов, число распространяющихся мод.
В практике волоконно-оптической гироскопии важно иметь оценочные характеристики волокон различной структуры, не прибегая к сложным расчетам представлять общую модель ошибок, которые могут заметно снизить точностные характеристики системы. Получим приближенные соотношения для статистических характеристик потерь в волокнах с различными свойствами и структурой определяющей их. Так как многомодовые световоды имеют дисперсионные характеристики, сильно ограничивающие точность приборов остановимся на рассмотрении одномодовых волокон в составе общей теории распространения волн.
Рассмотрим механизм потерь мощности в одномодовом волоконном световоде. При распространении электромагнитной энергии вдоль нерегулярного световода часть световой мощности рассеивается. Часть рассеивающейся мощности перераспределяется между вперед и назад распространяющимися модами, а остальная часть излучается. Интерес представляет вывод выражений для определения численной оценки величины рассеивающейся мощности для волокон с известными характеристиками профиля показателя преломления и допусковыми значениями нерегулярностей.
Неоднородности нерегулярных световодов удобно представлять как источники вынужденных токов, находящихся внутри регулярного световода. При этом может быть описано возбуждение как направленных мод, так и поля излучения.
Нерегулярности световодов приводят к зависимости показателя преломления от продольной координаты, т.е. n=n(x,y,z). Полные электрическое и магнитное поля E (x,y,z) и H(x,y,z) в любой точке внутри нерегулярного световода связаны между собой уравнениями Максвелла для среды без источников. С другой стороны, эти поля можно представить в виде поля регулярного световода, в котором имеются источники тока :
![]() (2.1)
(2.1)
Здесь
![]() - волновое число в свободном пространстве;
- волновое число в свободном пространстве;
![]() - профиль того же световода без неоднородностей.
- профиль того же световода без неоднородностей.
Величину
![]() (2.2)
(2.2)
называют вынужденной плотностью тока, обусловленной неоднородностью. Источник вынужденного тока (2.2) существует только внутри области неоднородности и целиком определен при условии известности полного электрического поля Е. Если световод является слабонаправляющим и n » n, то поля мод являются приблизительно поперечными и в первом приближении можно считать, что E = Ex, а
![]() (2.3)
(2.3)
Индекс x означает поперечную компоненту поля, а n1 - показатель преломления сердцевины волокна, иначе n(a)= n1 при а<r, где r - радиус сердцевины волокна.
Таким образом из (2.2) и (2.3) имеем:
![]() (2.4)
(2.4)
В этом приближении не учтены все поляризационные эффекты, обусловленные неоднородностями, поскольку в рамках приближения слабонаправляющего световода поперечные поля всех мод ортогональны друг другу. В частности, поляризованная вдоль оси x чётная основная мода не может быть возбуждена нечётной или поляризованной вдоль оси y основной модой.
Подставив в (2.4) выражение для электрического поля в гауссовом приближении рассмотренном в [1], получим следующее выражение для плотности тока, если на неоднородность в круглом световоде падает основная мода, поляризованная вдоль оси x :
![]() , (2.5)
, (2.5)
где ![]() - фундаментальное решение скалярного волнового уравнения для поля основной моды, определяемой в зависимости от профиля показателя преломления .
- фундаментальное решение скалярного волнового уравнения для поля основной моды, определяемой в зависимости от профиля показателя преломления .
Вследствие того что, волоконные световоды, используемые в волоконной гироскопии, являются слабонаправляющими, т.е. относительная разность между максимальным и минимальным значениями профиля показателя преломления n ( r ) мала, векторы Е и H аппроксимируются решениями скалярного волнового уравнения. Постоянная распространения b основной моды, направляемой по световоду, ограничивается интервалом между двумя экстремумами, которые определяются значениями b для плоских волн. В бесконечных средах с показателями преломления n1 и n2 :
![]() , (2.6)
, (2.6)
где n1 , n2 - максимальное и минимальное значения показателя преломления n ( r ); ![]() - длина волны в вакууме.
- длина волны в вакууме.
В силу слабой канализации волн в световодах, т.е. n1 »n2 из (2.6) следует b » 2 p n / l, что совпадает с постоянной распространения плоской волны в направлении Z в бесконечной среде с показателем преломления n2 £ n £ n1 .
Таким образом, основная мода волоконного световода является квазипоперечной электромагнитной (Т) волной. В простейшем случае - это волна, однородно поляризованная только в одном направлении в отличии от мод высших порядков. Если обозначить направление поляризации через Х, поле в световоде можно представить в виде
![]()
![]() , (2.7)
, (2.7)
где ![]() - магнитная проницаемость среды;
- магнитная проницаемость среды;
![]() =
= ![]() - диэлектрическая проницаемость среды;
- диэлектрическая проницаемость среды;
![]() - диэлектрическая проницаемость вакуума.
- диэлектрическая проницаемость вакуума.
Здесь неявно подразумеваем временную зависимость ![]() . Компоненты поля Ey, Ez, Hx, Hzне учитываются поскольку они пренебрежимо малы, Y описывает пространственное изменение поля в плоскости, перпендикулярной оси световода. Следует отметить, что отражение плоской волны от границы раздела диэлектрических сред с близкими параметрами практически не чувствительно к поляризации падающей волны. Соответственно, и пространственное изменение поля Y должно быть нечувствительно к поляризационным эффектам, поэтому Y - решение скалярного волнового уравнения, т.е.
. Компоненты поля Ey, Ez, Hx, Hzне учитываются поскольку они пренебрежимо малы, Y описывает пространственное изменение поля в плоскости, перпендикулярной оси световода. Следует отметить, что отражение плоской волны от границы раздела диэлектрических сред с близкими параметрами практически не чувствительно к поляризации падающей волны. Соответственно, и пространственное изменение поля Y должно быть нечувствительно к поляризационным эффектам, поэтому Y - решение скалярного волнового уравнения, т.е.
![]() , (2.8)
, (2.8)
где:
![]()
n ( r ) - профиль показателя преломления; l - длина волны в вакууме.
Таким образом, основная мода описывается решением уравнения (2.8), соответствующим наибольшему b и ![]() , не зависящей от угла
, не зависящей от угла ![]() . Для регулярного световода n ( r ) не зависит от длины, в случае нерегулярного световода n=n(x,y,z).
. Для регулярного световода n ( r ) не зависит от длины, в случае нерегулярного световода n=n(x,y,z).
В практически интересных случаях применяют в одномодовых световодах оптические волокна как со ступенчатым, так и градиентным профилем. При этом наибольшее распространение получили оптические волокна с гауссовым и ступенчатым профилями. Эти волокна целесообразно применять и в волоконной гироскопии поэтому остановимся на их анализе подробнее.
При изготовлении световодов в следствии диффузии границы между оболочкой и сердцевиной реальные профили могут отличаться как от ступенчатого, так и от гауссова, занимая некоторое промежуточное положение (сглаженный ступенчатый профиль). При этом профиль показателя преломления представляют в виде :
![]() (2.9)
(2.9)
где 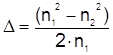 - параметр высоты профиля.
- параметр высоты профиля.
Численные решения волнового уравнения для ступенчатого и степенного профилей волокна [2] показывают, что форма Y (r) примерно гауссова. В соответствии с этими исследованиями поле моды HE11 можно представить в виде:
![]() (2.10)
(2.10)
где r0 - размер светового пятна, определенный вариационным методом в [2].
Для решения волнового уравнения умножим его на ![]()
и воспользуемся тождеством:
![]() (2.11)
(2.11)
После интегрирования в пределах от 0 до ¥ получаем
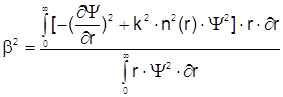 (2.12)
(2.12)
Кроме (2.12) появляется дополнительный член ![]() ,
,
который вычисляется при значениях r = 0 и ¥. Этот член равен нулю, поскольку ![]() конечно при r = 0 и экспоненциально стремиться к нулю при r ® ¥.
конечно при r = 0 и экспоненциально стремиться к нулю при r ® ¥.
Размер пятна r0 выбирается из условия обеспечения наибольшего b, которое соответствует основной моде. Подставляя приближенное выражение (2.10) в (2.12), можно определить r0 из условия db2/ dr0 = 0. Приближение для постоянной распространения b получается далее подстановкой найденного r0 в выражение (2.12). Таким образом, зная r0 и b можно полностью характеризовать поле с помощью формул (2.7) и (2.10). Используем полученную методику для определения параметров r0 и b для профилей применяемых в волокнах для оптической гироскопии.
В случае гауссова профиля показателя преломления:
![]() , (2.13)
, (2.13)
где
![]() .
.
Таким образом, n(r) с ростом r от 0 до ¥ уменьшается плавно от n1 до n2. Поскольку чёткой границы между сердцевиной и оболочкой нет, то форму профиля определяет радиус сердцевины a. Такая форма профиля показателя преломления представляет практический интерес, так как является хорошим приближением реального случая, когда в процессе изготовления волоконных световодов происходит взаимная диффузия материала сердцевины и оболочки.
Подставляя (2.13) в (2.10) и (2.12), из условия db2/dr0 = 0 находим величину
![]() (2.14)
(2.14)
Выражение (2.14) имеет физический смысл только при V >>1 (r0 - положительно), однако это не уменьшает его практической ценности, так как при V £ 1 вблизи оси световода распространяется лишь малая доля мощности основной моды. Подставляя r0 в (2.12) получаем выражение для
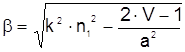 , (2.15)
, (2.15)
где
 (2.16)
(2.16)
Размер пятна r0 и постоянная распространения b полностью характеризуют поле основной моды, а следовательно, и передаточные свойства одномодовых световодов.
Распределение плотности мощности или профиль интенсивности S(r) имеет вид :
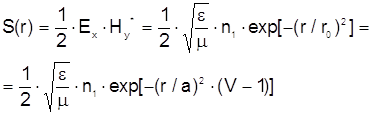 , (2.17)
, (2.17)
где e,m - относительная диэлектрическая и магнитная проницаемость вакуума.
С увеличением расстояния от оси световода интенсивность падает экспоненциально. При меньших значениях V спад происходит медленнее, поэтому чем меньше V, тем меньшая часть полной мощности распространяется вблизи оси волокна. Доля мощности, распространяющейся в интервале от 0 до r, равна
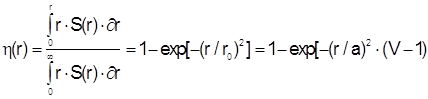 (2.18)
(2.18)
Таким образом в световодах с малым V распространяющееся излучение захватывает большую область поперечного сечения. Поскольку в практических ситуациях такое положение нежелательно, ограничение на V >1 (2.14) не важно. Практический интерес представляет определить ширину a профиля показателя преломления, при которой мощность пучка света будет наиболее сильно концентрироваться вблизи оси волокна при фиксированных значениях D и длины волны излучения, т.е. определить значение радиуса сердцевины, обеспечивающего минимальный размер пятна r0. Дифференцируя (2.14) по a и учитывая, что согласно (2.16) V пропорционально a, получим оптимальное значение a, соответствующее V=2, т.е.
![]() ) (2.19)
) (2.19)
При V = 2 имеем r0 = a, т.е. распределение интенсивности S(r) совпадает с формой профиля показателя преломления.
В случае световода со ступенчатым профилем показателя преломления:
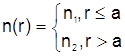 (2.20)
(2.20)
( S =1, f = 0 при r £ a и S =0, f =1 при r > a).
Следуя методике определения r0 и b для световодов с гауссовым профилем, получаем
![]() (2.21)
(2.21)
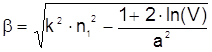 (2.22)
(2.22)
Все физические процессы имеющие место в волокнах с гауссовым профилем преломления, справедливы и для волокна со ступенчатым профилем. Радиус сердцевины a, обеспечивающий максимальную концентрацию света в волокне, определим в данном случае из условия V = exp(1/2) » 1.65 что соответствует
![]() (2.23)
(2.23)
Таким образом, плотность мощности в ступенчатом волоконном световоде выше на 17%. Доля мощности, распространяющейся в пределах радиуса r, будет равна
![]() (2.24)
(2.24)
Получим основные характеристики одномодовых световодов на основе выводов сделанных ранее. Рассмотрим амплитуду излучения и мощность распространяющихся мод.
Для j - й вперёд и назад распространяющихся мод полная мощность определяется соотношениями :
![]() (2.25)
(2.25)
![]() , (2.26)
, (2.26)
где Nj, N-j- параметры нормировки.
Полная мощность, возбуждённая во всех направляемых модах, будет равна
![]() (2.27)
(2.27)
Если световод является слабонаправляющим и круглым, а источники тока излучают вдоль оси x поперечного сечения световода, то мощность в каждой моде равна
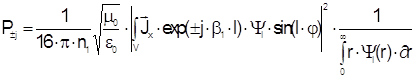 (2.28)
(2.28)
где bl- скалярные постоянные распространения;
Yl- решение скалярного волнового уравнения (2.11).
Для определения мощности излучения воспользуемся приближением свободного пространства, суть которого сводится к замене слабонаправляющего световода неограниченной однородной средой с показателем преломления оболочки n2 . В большинстве практических случаях излученная мощность достаточно точно описывается в рамках этого приближения.
Решение уравнений Максвелла для полного поля в световоде с произвольным показателем преломления, согласно методике, приведённой в [2], можно выразить через векторный потенциал А, декартовы составляющие которого удовлетворяют уравнению
![]() ,
(2.29)
,
(2.29)
где ![]() - распределение плотности тока; Ñ2 - скалярный оператор Лапласа. Решение уравнения (2.29) для каждой составляющей выражается через функцию Грина в виде
- распределение плотности тока; Ñ2 - скалярный оператор Лапласа. Решение уравнения (2.29) для каждой составляющей выражается через функцию Грина в виде
![]() , (2.30)
, (2.30)
где V - объём, в котором распределены источники тока;
![]() - радиусы-векторы точки наблюдения поля и точки расположения источника соответственно (рис 2.1.а).
- радиусы-векторы точки наблюдения поля и точки расположения источника соответственно (рис 2.1.а).
Функция Грина находится путём решения соответствующего уравнения для свободного пространства с показателем преломления n2 и имеет вид
![]() ,
(2.31)
,
(2.31)
где ![]() , а c - угол между векторами
, а c - угол между векторами ![]() и
и ![]() .
.
Подстановка (2.31) в (2.30) приводит к выражению
![]() , (2.32)
, (2.32)
где
![]()
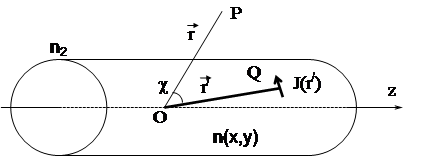
a)
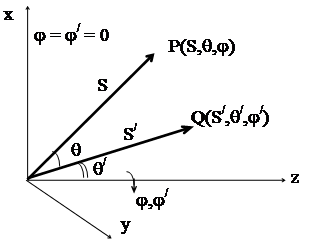
б)
Рис 2.1. Возмущение поля в точке P источником с плотностью тока J в точке Q (а) и сферические полярные координаты точек Р и Q (б).
Достаточно далеко в оболочке поля всех источников являются локально плоскими и имеют вид .
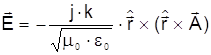 (2.33)
(2.33)
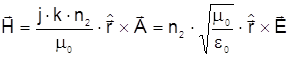 (2.34)
(2.34)
Отсюда запишем полную мощность излучения в виде
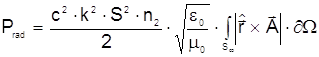 , (2.35)
, (2.35)
![]() где с - скорость света; S¥ - сферическая поверхность с радиусом ¥; W - пространственный угол; S = | r | - радиус среды;
где с - скорость света; S¥ - сферическая поверхность с радиусом ¥; W - пространственный угол; S = | r | - радиус среды;![]() - единичный вектор, параллельный радиальному вектору.
- единичный вектор, параллельный радиальному вектору.
Если векторы P и Q выразить в сферической системе координат (S,Q,j) (рис 1.б), которая ориентирована так, что если угол j равен нулю, радиус-вектор расположен в плоскости Z, то уравнение (2.35) с использованием (2.32) и (2.33) можно записать так
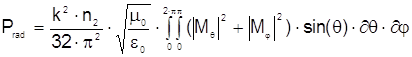 , (2.36)
, (2.36)
где Mq и Mj, q и j - составляющие вектора ![]() в точке Р
в точке Р
В случае поперечно-ориентированного источника (токи параллельны оси x) вектор ![]() будет иметь только составляющую Мх. Полную излученную мощность можно определить подстановкой в (2.36):
будет иметь только составляющую Мх. Полную излученную мощность можно определить подстановкой в (2.36):
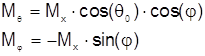 (2.37)
(2.37)
Здесь q0 - угол, под которым происходит излучение источника к оси световода. Из рис 2.1.б следует, что
![]() , (2.38)
, (2.38)
где a = S/ sin (q/) и z = S/ cos (q/) на трубке.
Подставляя (2.38) и (2.37) в (2.33) получаем
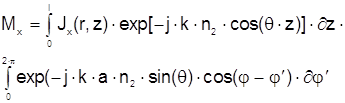 (2.39)
(2.39)
Интеграл по j/ является интегральным представлением функций Бесселя первого рода, нулевого порядка и тогда
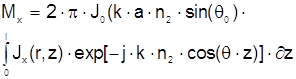 , (2.40)
, (2.40)
где J0(...) - функция Бесселя первого рода нулевого порядка.
Запишем величину плотности тока трубчатого источника (2.5) с учетом выражения полученного в [2]
![]() (2.41)
(2.41)
где DS(r,z) - отклонение функции профиля показателя преломления вследствие нерегулярностей.
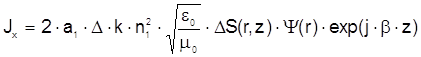 (2.42)
(2.42)
Подставив (2.41) в (2.40) получим
![]()
![]() , (2.43)
, (2.43)
где B = 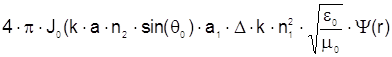
Поскольку Мx является случайной величиной, в (2.36) необходимо подставить средний квадрат <| Мx|2>. Воспользовавшись результатами полученными в [3] запишем
![]() , (2.44)
, (2.44)
где DDS - дисперсия функции профиля показателя преломления; rDS (t) - нормированная корреляционная функция распределения неоднородностей по длине световода DS (r,z).
При радиусе корреляции l0<<l
![]() , (2.45)
, (2.45)
где GDS (0) - спектральная плотность распределения неоднородностей по длине световода, определяемая соотношением :
![]() (2.46)
(2.46)
Поскольку аргумент спектральной плотности должен быть равен нулю, находим величину угла, под которым в среднем происходит излучение
![]() (2.47)
(2.47)
Полная средняя излученная мощность будет равна
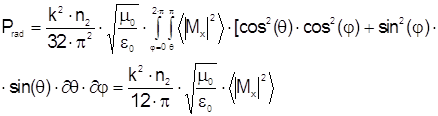 (2.48)
(2.48)
Таким образом, мы получили выражение для нахождения характеристик излученной мощности по известным статистическим характеристикам функций профиля показателя преломления, определяющих трубчатый источник тока DDS и GDS (0) или rDS (t).
Мощность основной моды P(z) на длине световода при наличии нерегулярностей затухает вследствие потерь на излучение. Если нерегулярный участок разделить на элементарные участки длиной dz, малые по сравнению с длиной z, то можно записать выражение для потери мощности моды на участке длиной dz:
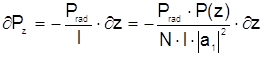 , (2.49)
, (2.49)
в котором использовались соотношения (2.25),(2.26)
![]() ,
(2.50)
,
(2.50)
где a1 - амплитуда моды; N - параметр нормировки.
Интегрируя (50) по длине l, получаем:
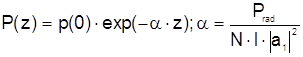 [Нп/км], (2.51)
[Нп/км], (2.51)
где a - коэффициент затухания мощности.
Подстановка выражения для N с произвольным профилем,
![]() ,
,
где R0 = r0 / a и использование выражения (2.51) дают
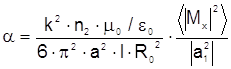 (2.52)
(2.52)
Полученное выражение даёт возможность, подставляя R0 для различных профилей показателя преломления, определять коэффициенты затухания вследствие потерь мощности на излучение для любого профиля показателя преломления.
В практике волоконно-оптических гироскопов интерес представляют волокна с различными профилями показателя преломления. Определим необходимые для разработчиков устройства параметры волокон используемых в этой области.
Рассмотрим световод со ступенчатым профилем показателя преломления, в котором граница между сердцевиной и оболочкой по длине деформирована случайным образом, т.е.
r(z) = a + F(z) , (2.53)
где а - радиус сердцевины регулярного световода;
F(z) - функция искажения границы, которая может отражать изгибы оси, изменение радиуса сердцевины или эллиптичность поперечного сечения.
При этом в случаях
искривления оси:
F(z) = f(z) / a (2.54)
отклонения радиуса:
F(z) = - x(z) / a, (2.55)
эллиптичности:
F(z) = - h(z) cos 2j / a. (2.56)
На рис 2.2. показано изменение радиуса сердцевины. Отклонение показателей преломления регулярного и нерегулярного световодов Dn = n - ![]() изменяется как ± (n1 - n2) в области нерегулярностей и равно нулю во всех остальных областях. Поскольку отклонения F(z) малы, можно предположить , что вынужденные токи сосредоточены в области границы сердцевины с оболочкой, поэтому имеем:
изменяется как ± (n1 - n2) в области нерегулярностей и равно нулю во всех остальных областях. Поскольку отклонения F(z) малы, можно предположить , что вынужденные токи сосредоточены в области границы сердцевины с оболочкой, поэтому имеем:
Dn = (n1 - n2) d (r-a) F(z), (2.57)
a
DS = F(z). (2.58)

Рис 2.2. Нерегулярный ступенчатый световод со случайными колебаниями радиуса сердцевины и эквивалентное распределение токов.
Таким образом, нерегулярный световод заменяем регулярным, возбуждаемым трубчатым источником тока, радиус которого равен радиусу сердцевины световода, ток направлен параллельно оси x, а амплитуда его определяется выражением (2.57).
Корреляционная функция DS будет равна
![]() ,
,
где rF (t) - нормированная корреляционная функция распределения неоднородностей по длине.
Дисперсия DS равна
DDS = KDS(0) = DF,
а соответствующая rF (t) спектральная плотность имеет вид:
![]()
В случае гауссова профиля отклонение функции профиля показателя преломления определяется выражениями полученными в [2]:
изменения радиуса сердцевины
DS(r,z) = (2 r2 / a3) x(z) exp [-(r/a)2]
случайные изгибы оси
DS(r,z) = (2 r/ a2) x(z) exp [-(r/a)2]
эллиптичность сердцевины
S(r,z) = exp [-(r/(a+h(z)cos 2j)]
Определим статистические характеристики DS
для изменения радиуса сердцевины
DDS = ( 4r4/ a6 )Dx exp [-2(r/a)2] (2.59)
rDS (t) = rx (t)
для случайных изгибов оси:
DDS = ( 4r2/a4Dfexp [-2(r/a)2]
rDS (t) = rf(t)
для эллиптичности
DDS = ( 2r4/a6Dhexp [-2(r/a)2]
rDS (t) = rh(t)
Для световодов со степенным профилем показателя преломления отклонение функции профиля преломления описывается выражением :
DS(r,z) = - [q (r/a)q x(z)]/a
для флуктуаций радиуса,
DS(r,z) = q (r/a)q f(z)]/r
для случайных изгибов и эллиптичности,
Исходя из этих выражений запишем:
для флуктуаций радиуса:
DDS = (q2/a2)(r/a)2q Dx
rDS(t) = rx(t)
для случайных изгибов оси
DDS = (q2/a2)(r/a)2q Df
rDS (t) = rf(t)
для эллиптичности
DDS = (q2/2a2)(r/a)2q Dh
rDS(t) = rh(t)
На основании полученных выражений можно проводить оценку статистических характеристик волокон с различными профилями показателя преломления. Численная оценка параметров волокна обеспечивающего одномодовый режим работы показывает, что с уменьшением радиуса корреляции нерегулярностей (точности изготовления и эксплуатационных параметров) коэффициент затухания падает, причём у световодов со ступенчатым профилем показателя преломления его относительная величина превышает коэффициент затухания световода с гауссовым профилем примерно в 1.6 раза. (рис 2.3.)
В волоконно-оптической гироскопии целесообразно использование импульсной модуляции для повышения точности детектирования и дальнейшей обработки сигналов. В связи с этим представляет интерес оценка искажения импульсов при наличии различного рода неоднородностей в волоконном контуре, которые приводят к появлению невзаимностей для лучей бегущих во встречных направлениях.
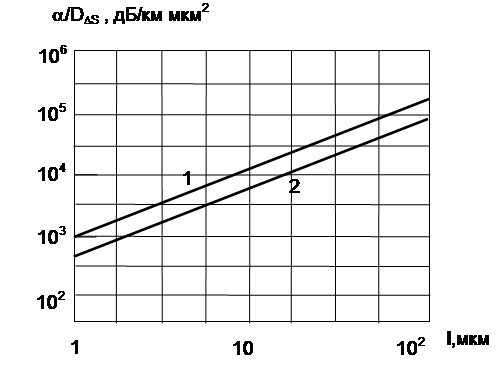
Рис 2.3. Зависимость коэффициента затухания от радиуса корреляции нерегулярностей функции профиля показателя сердцевины : 1 - для ступенчатого профиля; 2 - для гауссова профиля.
(n1=1.5; D=0.01;l=1.3 мкм; V=2.4;a=2.3 мкм)
Импульсы конечной длительности, возбуждаемые реальными источниками, обладают протяженным спектром и по мере распространения по световоду уширяются, что связано как с частотной зависимостью показателя преломления, так и с волноводной (внутримодовой) дисперсией, обусловленной нелинейной зависимостью b от частоты. Оба эффекта в зависимости от природы материальной дисперсии могут комбинироваться различным образом и при определённых длинах волн обычно компенсируются .
Рассмотрим влияние волноводной дисперсии на уширение импульсов. Среднюю скорость распространения импульсного сигнала по волокну определяет групповая скорость
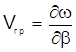 (2.60)
(2.60)
которая может быть получена для различных профилей показателя преломления дифференцированием выражений для b .
Для
гауссова профиля :
1/Vгр = (wmaea1 /b)(1-2D/V)
ступенчатого профиля :
1/Vгр = (wmaea1 /b)(1-2D/V2) (2.61)
сглаженного ступенчатого профиля :
1/Vгр = (wmaea1 /b)(1-2D/V2(m+1)/(m+2))
Степень отклонения групповой скорости от полученных значений определит отклонение коэффициента распространения вследствие нерегулярностей. Отклонение коэффициента распространения вследствие нерегулярностей в случае гауссова профиля определяется в зависимости от вида нерегулярностей. Воспользуемся полученными выражениями [2].
Для
изменения радиуса сердцевины
![]()
случайных изгибов
![]() (2.62)
(2.62)
случайной эллиптичности
![]() ,
,
где l0f , l0e, l0h - радиусы корреляции соответствующих нерегулярностей.
Для ступенчатого профиля показателя преломления :
![]() (2.63)
(2.63)
где DF и l0 - дисперсия и радиус корреляции соответствующих неоднородностей.
Численный анализ соотношений позволяет сделать выводы о том, что при прочих равных условиях наибольшее влияние на дисперсионные характеристики световодов с гауссовым профилем показателем преломления оказывают случайные изгибы оси световода, которые превышают действие нерегулярностей отражающей границы как минимум на порядок. Меньшее влияние оказывает эллиптичность сердцевины световода. Дисперсия отклонений уширения импульсов для волокон со ступенчатым профилем показателя, вне зависимости от вида нерегулярностей, одного порядка со случайными изгибами оси световода с гауссовым профилем показателя преломления.
Таким образом полученные соотношения описывают математическую модель нерегулярных одномодовых волоконных световодов с произвольной формой поперечного сечения и произвольным профилем показателя преломления. При этом не требуется привлечение сложного математического аппарата, численных или графических методов. Это дает возможность наиболее просто анализировать особенности технологии изготовления различных волоконных световодов и принимать решения по улучшению их качественных характеристик при использовании в волоконной гироскопии.
Оценим потери мощности и уширение импульсного сигнала в одномодовом ступенчатом оптическом волокне dс = (5±0.01) мкм со случайными колебаниями радиуса сердцевины (радиус корреляции примем типичным для современных волокон изготавливаемых зарубежом l0x = 0.01 мкм ). Показатель преломления сердцевины n1= 1.5; показатель преломления оболочки - n2 = 1.495 мкм.
Величину коэффициента затухания мощности определим по выражению (2.52) . Радиус светового пятна r0 находим по формуле (2.21), принимая V=2.4. Дисперсию функции колебания радиуса Dx определим из условия нормального закона распределения x(z): Dx = (0.005/3)2 = 2.78 10-6 мкм2 . Соответственно DDS находим по (2.59) . Угол, под которым происходит излучение, принимаем равным нулю, вследствие чего функция Бесселя равна 1 , а потери мощности по (2.52) будут равны »0.6 дБ/км.
Уширение импульса вследствие волноводной дисперсии находим по (2.63) . Подстановка численных значений даёт
DDt(l) = 3.02 10-8 x l пс2 , а максимальное уширение импульса на длине l ( l в км ) будет равно Dtmax = ±5.2 10-4 ![]() пс.
пс.
Полученные значения позволяют оценить невзаимность условий распространения волн бегущих во встречных направлениях и сделать вывод о необходимости точного соблюдения технологии изготовления волокон и обеспечения требуемых технологических параметров при сборке волоконного контура и его дальнейшей эксплуатации.
Как уже отмечалось, в круглом одномодовом световоде основная мода может существовать в двух ортогональных поляризациях ![]() и
и ![]() . В идеальном аксиально-симметричном и свободном от механических напряжений волоконном световоде эти моды вырождены. В реальных световодах наблюдается различие в постоянных распространения указанных мод, вызванное отклонением геометрии от идеальной и различием в значениях остаточных напряжениях в направлениях x и y. Остаточные напряжения являются результатом процесса вытяжки световода. Наличие связи между двумя ортогонально поляризованными модами приводит к вращению плоскости поляризации вдоль оси световода. Определенное состояние поляризации может сохраняться в круглом волоконном световоде на длине не более чем несколько метров.
. В идеальном аксиально-симметричном и свободном от механических напряжений волоконном световоде эти моды вырождены. В реальных световодах наблюдается различие в постоянных распространения указанных мод, вызванное отклонением геометрии от идеальной и различием в значениях остаточных напряжениях в направлениях x и y. Остаточные напряжения являются результатом процесса вытяжки световода. Наличие связи между двумя ортогонально поляризованными модами приводит к вращению плоскости поляризации вдоль оси световода. Определенное состояние поляризации может сохраняться в круглом волоконном световоде на длине не более чем несколько метров.
В волоконно-оптических гироскопах для решения этой проблемы на входе и выходе волоконного контура помещают специальное устройство - поляризатор, позволяющее отфильтровать моды с нежелательной поляризацией. Параметры этого устройства не идеальны, к тому же при распространении энергии по волокну происходит взаимодействие мод с различными поляризациями что приводит к изменению уровней сигналов а следовательно и фазовых задержек. Необходимо обеспечить распространение по волокну сигнала только с одной поляризацией и тем самым снизить требования к поляризатору и устранить взаимное влияние мод друг на друга .
Разработаны однополяризационные световоды с линейной и круглой поляризациями. Световоды с линейной поляризацией представляют собой аксиально-несимметричные структуры, в которых может распространяться или мода только одной поляризации, или две моды различной поляризации, но с большой разностью между значениями постоянных распространения этих мод. Первые являются абсолютно поляризационными световодами, вторые - световодами с линейным двулучепреломлением.
Устойчивость поляризации в световоде можно реализовать, если использовать двухслойные прямоугольные эллиптические световоды или круглые световоды с осесимметричным распределением показателя преломления. В этих световодах снимается вырождение ортогонально поляризованных мод, и две ортогональные компоненты фундаментальной моды будут иметь разные фазовые постоянные распространения. Это уменьшит связь по мощности между двумя поляризациями и, следовательно, уменьшит преобразование мод на нерегулярностях.
Вырождение можно снять комбинацией геометрической анизотропии и (или) анизотропии силовых напряжений в поперечной xy-плоскости световода. Можно вводить либо геометрическую эллиптичность сердечника волокна, либо индуцированное двулучепреломление материала световода.
В последнем случае для изготовления световода можно использовать разнородные материалы с различными температурными коэффициентами расширения. Это позволит вводить анизотропию напряжений в волокно посредством эффекта фотоупругости, что приводит к соответствующему двулучепреломлению. При изготовлении такого волокна оболочка (SiO2) легируется В2O3 , можно использовать также GeO2 . P2O5 . Сердечник изготавливается из безпримесного кремния. Вследствие разных коэффициентов термического расширения и поверхностных натяжений получаемое волокно имеет цилиндрический сердечник, эллиптическую внутреннюю оболочку и круговое внешнее покрытие. При такой структуре наблюдается сильная анизотропия напряжений. Мерой этой анизотропии является так называемое модальное двулучепреломление:
![]() (2.64)
(2.64)
Чем больше модальное двулучепреломление В, тем меньше связь между поляризационными модами.
Для количественного измерения В часто вводят новое понятие - так называемую «длину биений» Lб, связанную с модальным двулучепреломлением соотношением:
![]() (2.65)
(2.65)
или
![]()
Длину биений Lб можно непосредственно измерить несколькими способами (например, модуляционным способом). Требуемое большое значение модального двулучепреломления В, существенно уменьшающее поляризационную связь, будет определять весьма малое значение длины биений Lб (длина биений должна быть много меньше критического периода возмущений,действующих на волокно).
Таким образом, наилучшим способом обеспечения работы световода на одной собственной поляризационной моде является увеличение двулучепреломления между двумя собственными поляризационными модами. В соответствии с этим возможны три структуры волокна.
В первой структуре предлагается использовать геометрически асимметричный профиль показателя преломления (рис 2.4.). Двулучепреломление, обусловленное асимметричным профилем показателя преломления, не всегда достаточно для ряда применений: кроме того в этой структуре трудно уменьшить потери, так как на границе сердечник-оболочка имеет место резкий перепад показателя преломления.
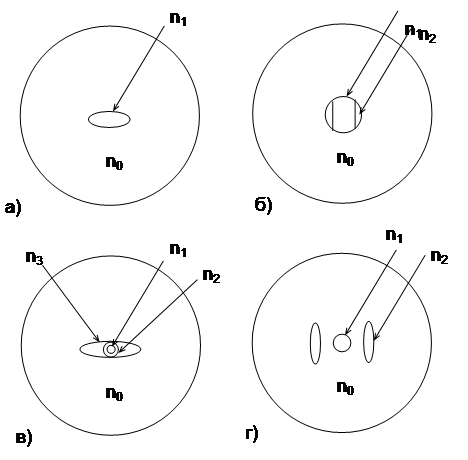
Рис 2.4. Структуры одномодовых световодов с устойчивой поляризацией: а - волокно с эллиптическим сердечником; б - волокно с боковым ячеечным распределением показателя преломления; в - волокно с эллиптической внешней оболочкой; г - волокно с боковым ячеечным напряжением.
Во второй структуре предлагается использовать двулучепреломление, индуцированное внеосевым внутренним напряжением. Эта структура имеет большие преимущества, чем структуры с простой анизотропией профиля, как с точки зрения увеличения двулучепреломления, так и вследствие уменьшения потерь. Длина биений менее 1 мм может быть получена в волокне с эллиптической оболочкой, легированной ![]() . В волокне, структура которого показана на рис 2.4.г, составляют порядка 0.3-0.5 дБ/км. В таких световодах распределенные перекрестные искажения между двумя линейно-поляризованными модами определяются, главным образом, случайными изгибами и скрутками.
. В волокне, структура которого показана на рис 2.4.г, составляют порядка 0.3-0.5 дБ/км. В таких световодах распределенные перекрестные искажения между двумя линейно-поляризованными модами определяются, главным образом, случайными изгибами и скрутками.
Дисперсия поляризованной моды в этих световодах составляет (0.1...2) нс/км, что все же велико по сравнению с обычным одномодовым волокном. Но в волоконно-оптическом гироскопе принципиальное значение имеют не потери в волокне, а невзаимность условий прохождения лучей в противоположных направлениях, что по существу и определяется именно искажениями поляризованных мод. Именно поэтому применение в ВОГ волокон с устойчивой поляризацией могут заметно снизить погрешности гироскопа и повысить его чувствительность.
При изготовлении одномодовых световодов с устойчивой поляризацией применяют также комбинированные структуры, сочетающие принцип создания двулучепреломления как с по мощью геометрической асимметрии анизотропии, так и с помощью напряжений.
Третья структура одномодового световода с устойчивой поляризацией использует крученое одномодовое волокно. Эта структура волокна отличается от рассмотренных выше тем, что две собственные поляризационные моды являются циркулярно поляризованными, а не линейно-поляризованными. Длина биений крученого волокна 5..10 см при частоте скрутки в несколько оборотов (5..15) на метр.
Это значение длины биений очень велико по сравнению с достигнутым для волокна с внеосевым напряжением. Поляризационное состояние в крученном волокне сохраняется на длинах волокна 1...1,2 км при любой входной поляризации (это достаточно для использования в ВОГ). Объясняется это тем, что модовая дисперсия в крученном волокне уменьшается с увеличением частоты скрутки, и поэтому нежелательные поляризационные компоненты могут быть исключены фазовой компенсацией. Модовые перекрестные искажения в крученом волокне между двумя циркулярно поляризованными модами определяются главным образом изгибами. Крученое волокно более чувствительно к внешним возмущениям, что объясняется относительно большой длиной биений.
Таким образом можно сделать важный вывод о том, что использование волокон с сохранением поляризации в ВОГ имеет две стороны. С одной стороны, оно позволяет существенно повысить чувствительность устройства засчет снижения поляризационных искажений и невзаимностей, но с другой увеличивает требования налагаемые на режим эксплуатации прибора и делает необходимым более точное изготовление всех его элементов и сохранение постоянными параметров окружающей среды (температурные градиенты, магнитные и электрические поля).
Похожие работы
... большие габариты, малый КПД, потребность во внешнем устройстве накачки являются основными причинами, по которым этот источник не используется в современных ВОСП. Практически во всех волоконно-оптических системах передачи, рассчитанных на широкое применение, в качестве источников излучения сейчас используются полупроводниковые светоизлучающие диоды и лазеры. Для них характерны в первую очередь ...
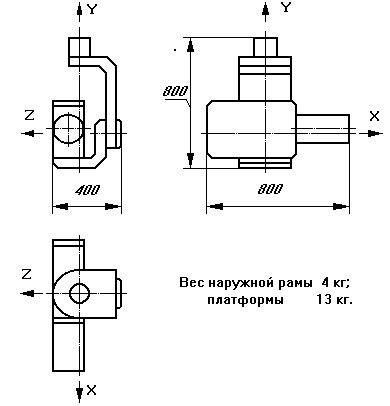
... за счет использования двигателя стабилизации меньших габаритов, имеющего меньший момент сухого трения вокруг оси вращения и меньший коэффициент демпфирования. Габаритные размеры гиростабилизатора телекамеры с наружным кардановым подвесом оказываются меньше, чем с внутренним, т.к. в последнем случае для получения достаточных рабочих углов поворота платформы необходимо выполнение подвеса по ...
... , подобных квантовым точкам, обещает большую точность и снижение стоимости путем использования методов производства, разработанных для полупроводниковой промышленности [2]. Приложения современных нанотехнологии в медицине Сегодня мы еще довольно далеки от описанного Фейнманом микроробота, способного через кровеносную систему проникнуть внутрь сердца и произвести там операцию на клапане. ...

0 комментариев