Составление уравнений

2. Составление уравнений.

система с ожиданием в случае простейшего потока и показательного времени обслуживания представляют собой случайный процесс Маркова.

Найдём те уравнения, которым удовлетворяют вероятности P_k(t). Одно из уравнений очевидно, а именно для каждого t

. (2)

Найдем сначала вероятность того, что в момент t+h все приборы свободны. Это может произойти следующими способами:

в момент t все приборы были свободны и за время h новых требований не поступало;

в момент t один прибор был занят обслуживанием требования, все остальные приборы свободны; за время h обслуживание требования было завершено и новых требований не поступило.

Остальные возможности, как-то: были заняты два или три прибора и за время h работа на них была закончена - имеют вероятность o(h), как легко в этом убедится.

Вероятность первого из указанных событий равна

вероятность второго события

Таким образом,

Отсюда очевидным образом приходим к уравнению

(3)

Перейдем теперь к составлению уравнений для P_k(t) при k ³ 1. Рассмотрим отдельно два различных случая: 1 £ k < m и k ³ m. Пусть вначале 1 £ k < m. Перечислим только существенные состояния, из которых можно прийти в состояние E_k в момент t+h. Эти состояния таковы:

В момент t система находилась в состоянии E_k, за время h новых требований не поступило и ни один прибор не окончил обслуживания. Вероятность этого события равна

В момент t система находилась в состоянии E_k-1, за время h поступило новое требование, но ни одно ранее находившееся требование не было закончено обслуживанием. Вероятность этого события равна

В момент t система находилась в состоянии E_k+1 , за время h новых требований не поступило, но одно требование было обслужено. Вероятность этого равна

Все остальные мыслимые возможности перехода в состояние E_k за промежуток времени h имеют вероятность, равную 0(h).

Собрав воедино найденные вероятности, получаем следующее равенство:

Несложные преобразования приводят нас к такому уравнению для 1 £ k < m:

(4)

Подобные же рассуждения для k ³ m приводят к уравнению

` (5)

Для определения вероятностей P_k(t) мы получили бесконечную систему дифференциальных уравнений (2)-(5). Ее решение представляет несомненные технические трудности.

3. Определение стационарного решения.

В теории массового обслуживания обычно изучают лишь установившееся решение для t ® ¥. Существование таких решений устанавливается так называемыми эргодическими теоремами, некоторые из них позднее будут нами установлены. В рассматриваемой задаче оказывается, что предельные или, как говорят обычно, стационарные вероятности существуют. Введем для них обозначения P_k . Заметим дополнительно, (этого мы также сейчас не станем доказывать), что  при t®¥.

Сказанное позволяет заключить, что уравнения (3), (4) и (5) для стационарных вероятностей принимают следующий вид:

(6)

при 1 £ k < m

(7)

при k ³ m

(8)

К этим уравнениям добавляется нормирующее условие

(9)

Для решения полученной бесконечной алгебраической системы введем обозначения: при 1£ k<m

при k ³ m

Система уравнений (6)-(8) в этих обозначениях принемает такой вид:

z₁=0, z_k-z_k+1=0 при k ³ 1

Отсюда заключается, что при всех k ³ 1 z_k =0

т.е. при 1 £ k < m

kmP_k=lP_{k-1 (10)}

_{и при k ³ m}mmP_k=lP_{k-1 (11)}

Введем для удобства записи обозначение

r=l/m.

Уравнение (10) позволяет заключить, что при 1 £ k < m

(12)

При k ³ m из уравнения (11) находим, что

и следовательно, при k ³ m

(13)

Остается найти P₀. Для этого в (9) подставляем выражения P_k из (12) и (13). В результате

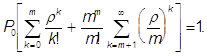
Так бесконечная сумма, стоящая в квадратных скобках, находится только при условии, что

r < m (14)

то при этом положении находим равенство

(15)

Если условие (14) не выполнено, т.е. если r ³ m, то ряд, стоящий в квадратной скобке уравнения для определения P₀ , расходится и, значит, P₀ должно быть равно 0. Но при этом, как следует из (12) и (13), при всех k ³ 1 оказывается P_k =0.

Методы теории цепей Маркова позволяют заключить, что при r ³ m с течением времени очередь стремится к ¥ по вероятности.