Навигация
6 К 6
| A¢1 |
| A2 |
4
| A3 |
2
| A4 |
| B2 |
| B1 |
y Решение. Матрица имеет размерность 2 х 4. Строим прямые, соответствующие стратегиям игрока 1. Ломанная А1 K А¢4 соответствует верхней границе выигрыша игрока 1, а отрезок N K –цене игры. Решение игры таково
U = (
; 
); Х = (
; 0; 0; 
); u = 
.
Сведение матричной игры к задаче линейного программирования
Предположим, что цена игры положительна (u > 0). Если это не так, то согласно свойству 6 всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.
Итак, пусть дана матричная игра с матрицей А порядка m х n. Согласно свойству 7 оптимальные смешанные стратегии х = (х1, ..., хm), y = (y1, ..., yn) соответственно игроков 1 и 2 и цена игры u должны удовлетворять соотношениям.
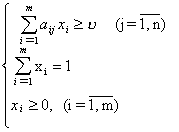
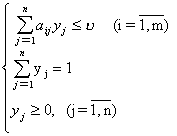
Разделим все уравнения и неравенства в (1) и (2) на u (это можно сделать, т.к. по предположению u > 0) и введём обозначения :
, 
,
Тогда (1) и (2) перепишется в виде :
, 
, 
, 
,
, 
, 
, 
.
Поскольку первый игрок стремится найти такие значения хi и, следовательно, pi , чтобы цена игры u была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений pi 
, при которых
, 
.
Поскольку второй игрок стремится найти такие значения yj и, следовательно, qj, чтобы цена игры u была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений qj, 
, при которых
, 
.
Формулы (3) и (4) выражают двойственные друг другу задачи линейного программирования (ЛП).
Решив эти задачи, получим значения pi 
, qj 
и u.Тогда смешанные стратегии, т.е. xi и yj получаются по формулам :
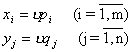
Пример. Найти решение игры, определяемой матрицей.
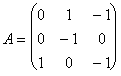
Решение. При решении этой игры к каждому элементу матрицы А прибавим 1 и получим следующую матрицу
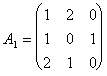
Составим теперь пару взаимно-двойственных задач :
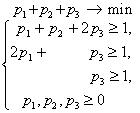
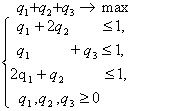
Решим вторую из них
|
| q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
| -1 | -1 | -1 | 0 | 0 | 0 | 0 | -3 | ||
|
| 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | — |
| q5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | — |
Б.п.
q4
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
|
| 0 | -1 | 0 | 0 | 1 | 0 | 1 | 1 | |
|
| 1 | 2 | 0 | 1 | 0 | 0 | 1 | 5 | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | — |
| q6 | 2 | 1 | 0 | 0 | 0 | 1 | 1 | 5 | |
q4
| Б.п. | q1 | q2 | q3 | q4 | q5 | q6 | Решение | å | Отношение |
|
| | 0 | 0 | | 1 | 0 | | | |
| q2 | | 1 | 0 | | 0 | 0 | | | |
| q3 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 4 | |
| q6 | | 0 | 0 |
| 0 | 1 | | |
Из оптимальной симплекс-таблицы следует, что
(q1, q2, q3) = (0;
; 1),
а из соотношений двойственности следует, что
( p1, p2, p3) = (
; 1; 0).
Следовательно, цена игры с платёжной матрицей А1 равна
. 
,
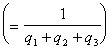а игры с платёжной матрицей А :
.
При этом оптимальные стратегии игроков имеют вид:
Х = (х1, х2, х3) = (uр1; uр2; uр3) = 
= 
Y = (y1, y2, y3) = (uq1; uq2; uq3) = 
= 
.
Похожие работы
... систем стимулирования. Она полезна также для формирования и развития внутрифирменных культур. Важный вклад в использование теории игр вносят экспериментальные работы. Многие теоретические выкладки отрабатываются в лабораторных условиях, а полученные результаты служат импульсом для практиков. Теоретически было выяснено, при каких условиях двум эгоистически настроенным партнерам целесообразно ...
... общую цель. Однако разные члены коллектива могут быть по-разному информированы об обстановке проведения игры. Выигрыш или проигрыш сторон оценивается численно, другие случаи в теории игр не рассматриваются, хотя не всякий выигрыш в действительности можно оценить количественно. Игрок - одна из сторон в игровой ситуации. Стратегия игрока - его правила действия в каждой из возможных ситуаций игры. ...
... запасов сырья, материалов, полуфабрикатов, когда противоборствуют две тенденции: увеличение запасов, гарантирующих бесперебойную работу производства, сокращения запасов в целях минимизации затрат на их хранение. В сельском хозяйстве теория игр может применяться при решении таких экономических задач, как посева одной из возможных культур, урожай которой зависит от погоды, если известны цена единицы ...
... , находящихся в обслуживающей системе, обслуживаемых и ожидающих обслуживания: или 8.Среднее число свободных обслуживающих каналов . 9.Коэффициент простоя обслуживающего канала: II. Практическое применение теории игр в задачах моделирования экономических процессах Пример №1 На базе торговой фирмы имеется n типов товара ассортиментного минимума. В магазин фирмы должен ...
0 комментариев