Колебаниями называются движения или процессы, которые характеризуются определённой повторяемостью во времени. Колебания бывают:
Вынужденные
Гармонические
Затухающие
Периодические
Внешняя сила, обеспечивающая незатухающие колебания системы, называется вынужденной, а колебания системы – вынужденными.
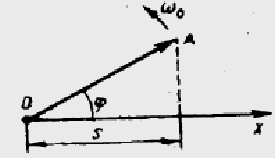
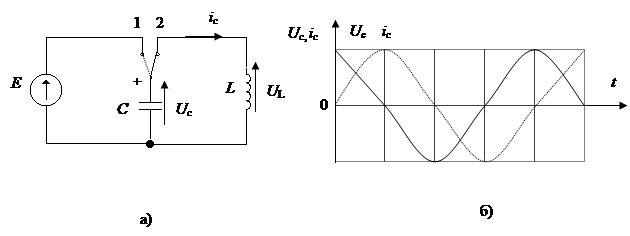
Гармоническим называют колебание, при котором изменение колеблющейся величины со временем происходит по закону синуса (или косинуса, если точка М (материальная точка) проецируется на горизонтальный диаметр).
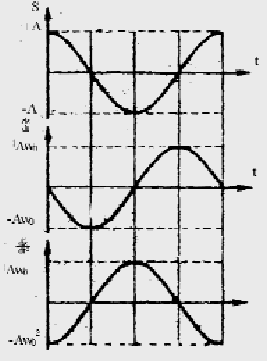
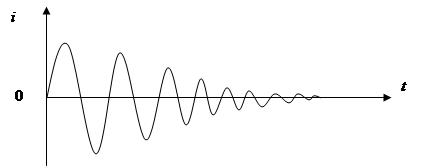
Колебательное движение реальной механической системы всегда сопровождается трением, на преодоление которого расходуется часть энергии колебательной системы. Поэтому энергия колебания в процессе колебания уменьшается, переходя в теплоту. Т.к. энергия колебания пропорциональна квадрату амплитуды, то постепенно уменьшается и амплитуда колебаний (см. Рисунок: х - смещение, t – время). Когда вся энергия колебания перейдёт в теплоту, колебание прекратится. Такого рода колебания называются затухающими.
Периодическим называется колебание, при котором, система отклоняется от своего состояния равновесия, и каждый раз возвращается к нему через одинаковые промежутки времени.
Колебательные процессы широко распространены в природе и технике: вибрация натянутой струны, движение поршня дизеля и ножей косилки, суточные и годичные изменения температуры воздуха, морские приливы и отливы, волнение водной поверхности, биение сердца, дыхание, тепловое движение ионов кристаллической решётки твёрдого тела, переменный ток и его электромагнитное поле, движение электронов в атоме, и, конечно, движение часового маятника. Рассмотрим колебания математического маятника:
Математическим маятником называется материальная точка, колеблющаяся на невесомой и недеформируемой нити.
Момент инерции математического маятника равен:
J = ml2 ,
Где m – масса материальной точки, l – длина нити.
Подставляя это выражение в выражение периода колебание маятника (T = 2 / = 2 J/(mgl)), получим окончательную формулу периода колебаний математического маятника:
T = 2 l/g.
Отсюда следует, что при малых отклонениях период колебания математического маятника пропорционален квадратному корню из длины маятника, обратно пропорционален квадратному корню из ускорения свободного падения и не зависит от амплитуды колебаний и массы маятника.
Колебательные явления могут возникать помимо нашего желания и играть вредную роль: часто наблюдаются нежелательные и опасные колебания сооружений, вибрации механизмов и т.д.
Список литературыР.И. ГРАБОВСКИЙ (Курс Физики)
О.Ю. ШМИДТ, Ф.Н. ПЕТРОВ (Большая Советская Энциклопе
Похожие работы
... колеблющуюся величину представляют комплексным числом. Согласно формуле Эйлера, для комплексных чисел (7) где - мнимая единица. Поэтому уравнение гармонического колебания (1) можно записать в комплексной форме: (8)вещественная часть выражения (8) представляет собой гармоническое колебание. Обозначение Re вещественной ...
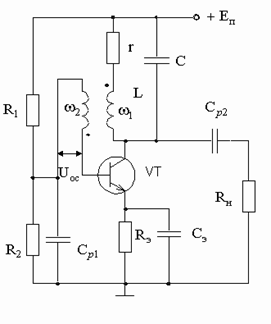
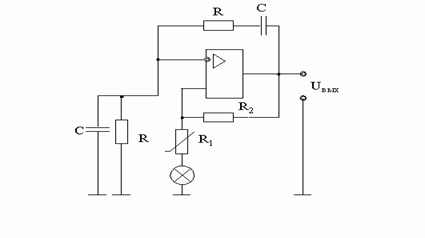
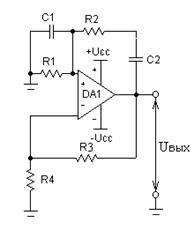
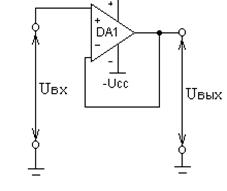
... систему, совершающую колебания). Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменятся со временем по закону синуса (косинуса). Генератором гармонических колебаний называют устройство, создающее переменное синусоидальное напряжение при отсутствии входных сигналов. В схемах генераторов всегда используется положительная обратная связь. ...
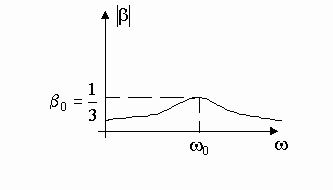
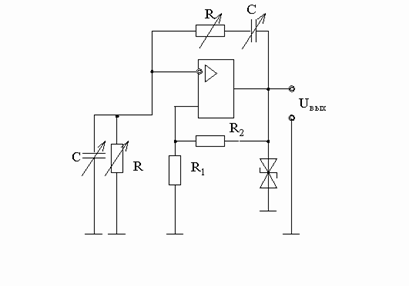
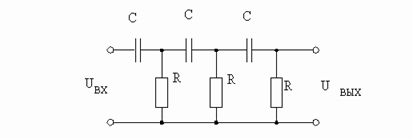
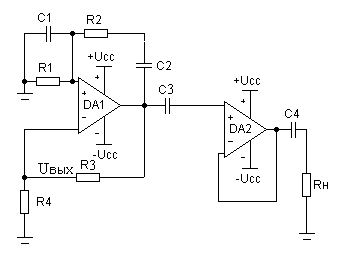
... колебаний, частоты которых достигают сотен килогерц. Учитывая все выше написанное и то, что необходимо выполнить генератор гармонических колебаний с частотой fг = 8 кГц. в качестве частотно избирательной цепочки ПОС выбираю RC-цепь, а усилительным элементом по заданию является операционный усилитель (ОУ). §3. Выбор RC-цепочки RC-цепочка может быть подключена как к инвертирующему, так и к ...
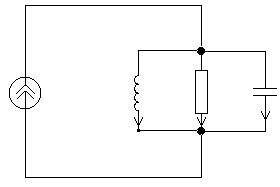
... контуров являются одним из основных, т.к. они зависят от первичных параметров, и их называют вторичными параметрами контура. Рис. 4 2. Возможные режимы установившихся гармонических колебаний в параллельном колебательном контуре Параллельным колебательным контуром называют цепь, составленную из элементов индуктивности, емкости и сопротивления, соединенных параллельно. Схема контура ...

0 комментариев