Навигация
X3 + 2/7 x4 + x5 – 5/14 x6– 2/7 x7 = 5
2 x3 + 2/7 x4 + x5 – 5/14 x6– 2/7 x7 = 5
x1 - Ѕ x3 + x4 + 2/7 x6 – 1/14 x7 = 31
(18)
x2 + x3 - 1/7 x4 – 1/14 x6 + 1/7 x7 = 12
4 x3 + 3 x4 + 8 x6 + 2x7 = 1500
- z
Первые три уравнения системы (18) представляют некоторый предпочитаемый
эквивалент системы уравнений (5) и определяют базисноенеотрицательное решение
системы условий рассматриваемой задачи
x1=37, x2=0, x3=0, x4=0, x5=29, x6=0, x7=84
(19)
т.е. определяют производственную программу x1=37, x2=0, x3=0, x4=0 (20)
и остатки ресурсов:
первого вида х5=5
второго вида х6=0
(21)
третьего вида х7=0
Последнее уравнение системы (18) мы получаем, исключая х2. В последнем уравнении
системы (18) среди коэффициентов принеизвестных в левой части уравнения нет ни
одного отрицательного. Если из этого уравнения выразить функцию цели z через
остальные неотрицательныепеременные
z = 1500 - 4 x3 - 3 x4 - 8 x6 - 2x7 (22)
то становится совершенно очевидным (в силу того, что все xj³0), чтоприбыль будет
наибольшей тогда, когда
x3=0, x4=0, x6=0, x7=0
(23)
Это означает, что производственная программа (20) является наилучшей и
обеспечивает предприятию наибольшую прибыль zmax= 1500
(24)
Итак, организовав направленный перебор базисных неотрицательных решений системы
условий задачи, мы пришли к оптимальнойпроизводственной программе и указали
остатки ресурсов, а также максимальную прибыль.
Следует обратить внимание на экономический смысл элементов последней строки
последней симплексной таблицы. Например, коэффициентD3=4 при переменной х3
показывает, что если произвести одну единицу продукциитретьего вида (она не
входит в оптимальную производственную программу), то прибыль уменьшится на 4
единиц.
Воспользуемся тем, что в оптимальной производственной программе x3=0, x4=0.
Предположим, что четвертую и третьюпродукции мы не намеревались выпускать с
самого начала. Рассмотрим задачу с оставшимися двумя переменными, сохранивих
нумерацию. Математическая модельзадачи будет выглядеть следующим образом:
Следует при этом обратить внимание на то, что последовательное улучшение
производственной программы (x1=0, x2=0) ® (x1=37,x2=0) ® (x1=31, x2=12) на
графике означает движение от одной вершины многогранникадопустимых решений к
другой вершине по связывающей их стороне многоугольника.
ДВОЙСТВЕННАЯЗАДАЧА
Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску
четырехвидов продукции с использованием трех видов ресурсов по заданным
технологиям.
Теперь представим себе, что знакомый предприниматель П, занимающийся
производством каких-то других видов продукции, но сиспользованием трех таких же
видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным
ценам все имеющиеся у нас ресурсы иобещает платить у1 рублей за каждую единицу
первого ресурса, у2 руб – второго, у3 руб – третьего. Возникает вопрос: при
каких ценаху1, у2, у3 мы можем согласиться с предложением П.
Величины у1, у2, у3принято называть расчетными, или двойственными, оценками
ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.
Напомним, что в нашей задаче технологическая матрица А, вектор объемов ресурсов
В и вектор удельной прибыли С имели вид
Для производства единицы продукции первого вида мы должны затратить, как видно
изматрицы А, 2 единицы ресурса первого вида, 4 единицы ресурса второго вида и 2
единицы третьего (элементы первого столбца матрицы). В ценах у1, у2,у3 наши
затраты составят 2у1 + 4у2 + 2у3, т.е. столько заплатит предприниматель П за все
ресурсы, идущие на производствоединицы продукции первого вида. На рынке за
единицу первой продукции мы получили бы прибыль 36 руб. Следовательно, мы можем
согласиться с предложениемП только в том случае, если он заплатит не меньше 2у1
+ 4у2 + 2у3 ³36.
Аналогично, для трех оставшихся видов продукции:
3у1 + 2у2 + 8у3³32
4у1 + 7у3³10
у1 + 2у2 ³13
Учтем, что за все имеющиеся у нас ресурсы нам должны заплатить 103у1 + 148у2 +
158у3рублей. При поставленных нами условиях предприниматель П будет искать такие
значения величин у1, у2, у3, чтобы эта суммабыла как можно меньше. Подчеркнем,
что здесь речь идет не о ценах, по которым мы когда-то приобретали этиресурсы,
а об этих ценах, которые существенно зависят от применяемых нами технологий,
объемов ресурсов и от ситуации на рынке.
Таким образом, проблема определения расчетных оценок ресурсов приводит к
задачелинейного программирования: найти вектор двойственных оценок у(у1, y2,
y3)минимизирующий общую оценку всех ресурсов f = 103у1 +
148у2 + 158у3 (1)
при условии, что по каждому виду продукции суммарная оценка всех ресурсов,
затрачиваемых на производство единицы продукции, неменьше прибыли, получаемой от
реализации единицы этой продукции
2у1 + 4у2 + 2у3 ³ 36
3у1 + 2у2 + 8у3³32 (2)
4у1 + 7у3³10
у1 + 2у2 ³13
причем оценки ресурсов не могут быть отрицательными y10, y20, y30. (3)
Решение полученной задачи легко найти с помощью второй основной теоремы
двойственности, согласно которой для оптимальных решений (х1, х2,
х3, х4) и (y1, y2, y3) парыдвойственных задач необходимо и достаточно
выполнение условий
x 1 (2у1 + 4у2 + 2у3 - 36) = 0 y1 (2x1 +3x2+ 4x3
+ x4 - 103) = 0
x 2 (3у1 + 2у2 + 8у3 - 32) = 0 y2 (4x1 +2x2
+ 2x4 - 148) = 0
x 3 (4у1 + 7у3- 10) = 0 y3 (2x1 +8x2 +
7x3 - 158) = 0 .
x 4 (у1 + 2у2 - 13) = 0
Ранее было найдено, что в решении исходной задачи х1>0, x2>0. Поэтому
2y1 +4y2 + 2y3 - 36 =
0
3y1 + 2y2
+8y3 - 32 = 0
Если же учесть, что первый ресурс был избыточным и, согласно той же теореме
двойственности, ее двойственная оценка равна нулю у1=0,
то приходим к системе уравнений
4y2 + 2y3 -36 = 0
2y2 + 8y3 - 32 = 0
откуда следует у2=8, у3=2.
Таким образом, получили двойственные оценки ресурсов у1=0; у2=8;
у3=2, (4)
причем общая оценка всех ресурсов равна 1500.
Заметим, что решение (4) содержалось в последней строке последней симплексной
таблицыисходной задачи. Важен экономический смысл двойственных оценок. Например,
двойственная оценка третьего ресурса у3=2 показывает, что добавлениеодной
единицы третьего ресурса обеспечит прирост прибыли в 2 единицы.
ЗАДАЧА О "РАСШИВКЕ УЗКИХ МЕСТ ПРОИЗВОДСТВА"
При выполнении оптимальной производственной программы второй и третий ресурсы
используются полностью, т.е. образуют ²узкиеместа производства². Будем их
заказывать дополнительно. Пусть T(t1,t2,t3)-вектор дополнительных объемов
ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов,
то должно выполняться условие H + Q-1T 0.
Задача состоит в том, чтобы найти вектор T (0, t2, t3), максимизирующий
суммарный приростприбыли W = 8t2 + 2t3
(1) при условии сохранения двойственныхоценок ресурсов (и,
следовательно, структуры производственной программы)
(2)
предполагая, что можно надеяться получить
дополнительно не более 1/3 первоначального объема ресурса каждоговида
(3)
причем по смыслу задачи t2 0, t3 0.
(4)
Переписав неравенства (2) и (3) в виде:
(5)
из условия (3) следует t2£148/3, t3£158/3 (6)
приходим к задаче ЛП: максимизировать (1) при условиях (5), (6) и (4).
Эту задачу легко решить графически: см. рис. 2. Программа ²расшивки² имеет вид
t1=0, t2=14, t3=0 и прирост прибыли составит 112.
Сводка результатов приведена в таблицe 2.
сj 36 32 10 13 b x4+i yi ti
2 3 4 1 103 5 0 0
aij 4 2 0 2 148 0 8 14
2 8 7 0 158 0 2 0
xj 31 12 0 0 1500 112
Dj 0 0 4 3
ТРАНСПОРТНАЯЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Однородный продукт, сосредоточенный в 3 пунктах производства (хранения) в
количествах 40;60; 70 единиц, необходимо распределить между 4 пунктами
потребления, которым необходимо соответственно 36; 32; 40; 53 единиц. Стоимость
перевозки единицыпродукта из пункта отправления в пункт назначения известна для
всех маршрутов и равна С = . Необходимо составить план перевозок, при
котором запросы всех пунктов потребления были бы удовлетворены за счет имеющихся
продуктов впунктах производства и общие транспортные расходы по доставке
продуктов были минимальными.
Для решения транспортной задачи чаще всего применяется метод потенциалов.
Общий объем производства åаi =40+60+70=170 больше, чемтребуется всем
потребителям åbi = 36+32 +40 +53 =161, т.е. имеем открытую модель транспортной
задачи. Для превращенияее в закрытую вводим фиктивный пункт потребления с
объемом потребления 170-161 = 9 единиц, причем тарифы на перевозку в этот пункт
условимся считать равныминулю, помня, что переменные, добавляемые к левым частям
неравенств для превращения их в уравнения, входят в функцию цели с нулевыми
коэффициентами.
Первое базисное допустимое решение легко построить по правилу ²северо-западного
угла².
Потребление b1 =36 b2 =32 b3 =40 b4 =53 b5 =9
Производство
а1 =40 36 4 p1 =0
a2 =60 28 32 p2 =
a3 =70 * 8 53 9 p3 =
q1 = q2 = q3 = q4 = q5 =
Общая стоимость всех перевозок для первого базисного допустимого решения:
L= 36* 2 + 4 *3 + 28 *2 + 32 + 8* 7+ 53 =281
Один из потенциалов можно выбрать произвольно, так как в системе (3), (4)
одноуравнение линейно зависит от остальных. Положим, что р1 = 0. Остальные
потенциалы находим из условия, что для базисных клеток . В данном случае
получаем
D11 = 0, p1 + q1 - c11= 0, 0+q1 -2 = 0,
q1 = 2
D12 = 0, p1 + q2 - c12= 0, 0+q2 -3 = 0,
q2 = 3
D22 = 0, p2 + q2 - c22 = 0, р2+3-2 = 0, р2 = -1
и т.д., получим: q3=2, p3=5, q4= -4, q5= -5.
Затем по формуле (6) вычисляем оценки всех свободных клеток:
D21 = p2 + q5 - c21 = -1+2-4 = -3
D31 = p3 + q1 - c31 = 5+2-2 = 5
D32 = 1; D13 =-2; D14 = -5; D24 =0; D15 = -5; D25 = -6.
Находим наибольшую положительную оценку max () = 5 =
Для найденной свободной клетки 31 строим цикл пересчета - замкнутую ломаную
линию, соседниезвенья которой взаимно перпендикулярны, сами звенья параллельны
строкам и столбцам таблицы, одна из вершин находится в данной свободной клетке,
а всеостальные - в занятых клетках. Это будет 31-11-12-22-23-33. Производим
перераспределение поставок вдоль цикла пересчета
36 4 36-r 4+r 28 12
28 32 28-r 32+r 20 40
8 r 8-r 8
= 8
Получаем второе базисное допустимое решение:
bj b1 =36 b2 =32 b3 =40 b4 =53 b5=9
ai
а1 =40 28 12 * p1 =0
a2 =60 20 40 p2 = -1
a3 =70 8 53 9 p3 =0
q1 =2 q2 = 3 q3 = 2 q4 = 1 q5=0
Находим новые потенциалы, новые оценки.
D13 = -2; D14 = 0; D15 = 0; D21 = -3; D24 = -2; D25 = -1; D32 = -4; D33 =
-5,
т.е. все Dij £ 0 i = 1,m; j = 1,n
Общая стоимость всех перевозок для второго базисного допустимого решения:
L= 28* 2 + 12 *3 + 20 *2 + 40 + 8* 2+ 53 =241 – минимальная стоимость.
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ. РАСПРЕДЕЛЕНИЕКАПИТАЛЬНЫХ ВЛОЖЕНИЙ
Пусть производственное объединениесостоит из четырех предприятий (n=4). Общая
сумма капитальных вложений равна700 тыс. рублей (b=700), выделяемые предприятиям
суммы кратны 100 тыс. рублей.Значения функций fj(xj) приведены в таблице 1, где,
например, число 50означает, что если третье предприятие получит 600 тыс. руб.
капитальныхвложений, то прирост прибыли на этом предприятии составит 50 тыс.
руб.
Таблица I
Прежде всего заполняем табл. 2. Значенияf2(x2) складываем со значениями F1(x -
x2) = f1(x- x2) и на каждойсеверо-восточной диагонали находим наибольшее число,
которое отмечаемзвездочкой и указываем соответствующее значение . Заполняем
таблицу 3.
Продолжая процесс, табулируем функцииF3(x), (x) и т.д. В табл. 6 заполняем
только одну диагональ для значения x=700.
Таблица 2
x - x2 0 100 200 300 400 500 600 700
x2 F1(x- x2)
f2(x2) 0 15 24 30 36 40 43 45
0
0 0 15 24 30 36 40 43 45
100 18 18* 33* 42* 48 54 58 61
200 26 26 41 50* 56 62 66
300 34 34 49 58* 64* 70*
400 39 39 54 63 69
500 42 42 57 66
600 44 44 59
700 46 46
Таблица 3
x 0 100 200 300 400 500 600 700
F2(x) 0 18 33 42 50 58 64
70
` (x)
0 0 100 100 200 300 300 300
Таблица 4
x- x3 0 100 200 300 400 500 600 700
x3 F2(x- x3)
f3(x3) 0 18 33 42 50 58 64 70
0
0 0 18* 33 42 50 58 64 70
100 16 16 34* 49* 58 66 74 80
200 27 27 45 60* 69 77 85
300 37 37 55 70* 79* 87*
400 44 44 62 77 86
500 48 48 66 81
600 50 50 68
700 56 56
Таблица 5
x 0 100 200 300 400 500 600 700
F3(x) 0 18 34 49 60 70 79
87
(x)
0 0 100 100 200 300 300 300
Таблица 6
x - x4 0 100 200 300 400 500 600 700
x4 F3(x- x4)
f4(x4) 0 18 34 49 60 70 79 87
0 0
87
100 10
89*
200 17 87
300 23 83
400 29 78
500 34 68
600 38 56
700 41 41
.
Наибольшее число на этой диагонали: Zmax = 89 тыс. руб.,
причем четвертому предприятию должно бытьвыделено х*4 = 4 (700) = 100 тыс.
руб.
На долю остальных трех предприятийостается 600 тыс. руб. Из табл. 5 видно, что
третьему предприятию должно бытьвыделено x*3 = 3 (700-x*4) = 3 (600) =
Похожие работы
... лучей, исходящих из одной точки, называется многогранным выпуклым конусом с вершиной в данной точке. 1.4 Математические основы решения задачи линейного программирования графическим способом 1.4.1 Математический аппарат Для понимания всего дальнейшего полезно знать и представлять себе геометрическую интерпретацию задач линейного программирования, которую можно дать для случаев n = 2 и n = ...
... решения останется неизменным, т.е. будет состоять из переменных (Х3,Х6,Х4,Х5). СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного программирования. Ч.1. – Мн.: БГУИР, 1995. 2. Смородинский С.С., Батин Н.В. Методы и алгоритмы для решения оптимизационных задач линейного ...
... . 1.3. Построение ограничений и градиента целевой функции : 1.4. Область допустимых решений – отрезок AB. 1.5. Точка А – оптимальная. Координаты т. А: ; ; . 2. Решение задачи линейного программирования симплекс-методом. Прямая задача. Задачу линейного программирования для любой вершины в компактной форме можно представить в виде: Для получения используем алгоритм, приведённый в ...
... к решению параметрической задачи квадратичного программирования. 55 5.Экономическая часть 57 6.Библиография 65 1. Введение В настоящей работе рассматривается применение метода субоптимизации на многообразиях к решению задачи квадратичного программирования с параметром в правых частях ограничений. Метод субоптимизации на многообразиях, предложенный У.Зангвиллом в 1968 году для решения задач ...





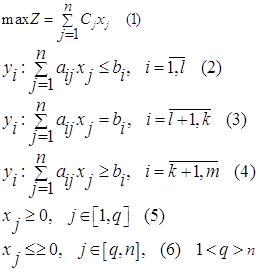
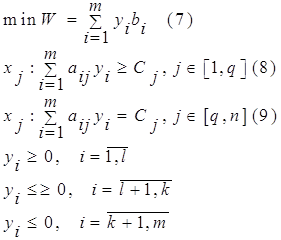
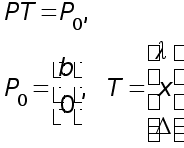
0 комментариев