Навигация
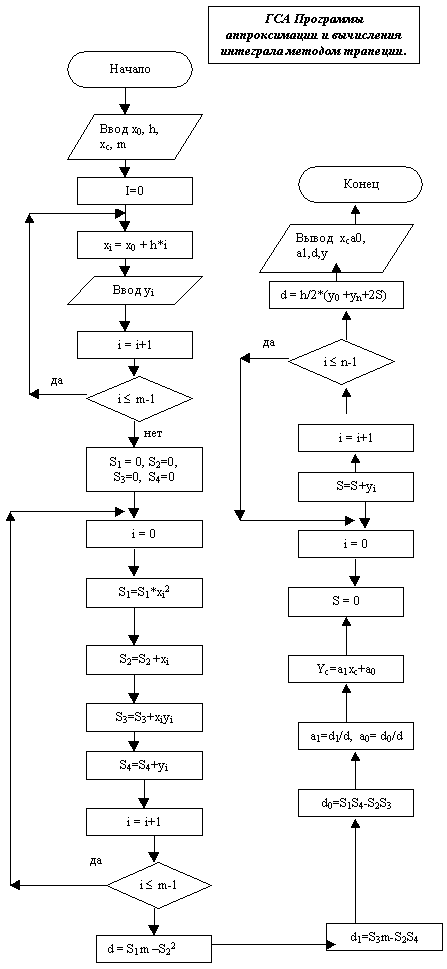
9.1 Выводы.
Данная программа очень эффективна, так как машина выполняет все действия гораздо быстрее, чем человек при ручном счете. Так же во время ручного счета могут произоити ошибки, что приведет к повторному перещитыванию, а у машины, при правильном алгоритме, таких сбоев не бывает (если только "зависает"). Следовательно эта программа во многом облегчает жизнь человеку.
II. Экономическая часть. Разработка модуля исключения нуль-уравнений в комплексе “Решение задачи линейного программирования”.
1.2 Постановка задачи линейного программирования и задание на разработку модуля.
Рассмотрим задачу оптимального планирования производства [1]. Пусть предприятие выпускает n изделий, для производства которых используется m ингредиентов. Ингредиенты это – детали определенного сортамента, станки, работники, электроэнергия и т.д., иначе говоря, все что требуется для осуществления производственного цикла. Запасы ингредиентов задаются вектором b=(b1, b2,…, bm ), где bi - запас i-го ингридиента (i=1,…,m). Задана матрица А, элемент которой aij определяет расход i-го ингридиента для производства единицы j-го изделия (i=1,…,m; j=1,…,n). Кроме того, задан вектор рыночных цен изделий p=(p1, p2,…, pn), где p - цена j-го изделия (j=1,…,n).
Требуется составить такой план производства х=(х1, х2,…, хn), чтобы при выполнение условий
| a11x1 + a12x2 + … + a1nxn £ b1 | ||
| ||
| …………………………….……………………. | ||
| am1x1 + am2x2 + … + amnxn £ bm | ||
| xj ³ 0, (j=1,…,n). |
достигался максимум функции
|
Z= p1x1 + p2x2 + … + pnxn
Функция Z называется целевой.
i-е ограничение из (1) означает, что нельзя израсходовать i-го ингредиента больше, чем имеется в наличии. Ограничения (1) задают множество W. Переменные, удовлетворяющие условию xj³0, называются несвободными. В нашей задаче это означает, что при xj=0 - ничего не производится или при xj>0 производится некоторое количество изделий.
Переменные, на которые условия неотрицательности не накладываются, называются свободными.
Задача (1)-(1') и есть задача оптимального производственного планирования, решение которой обеспечивает достижение в конкретных условиях максимальной прибыли.
Сформулируем двойственную к (1)-(1') задачу о приобритении ингридиентов по минимальной рыночной стоимости. Пусть то же самое предприятие, что и в задаче (1)-(1'), собирается приобрести на рынке m ингридиентов для производства тех же n изделий. При этом количество приобретаемых ингридиентов определяется вектором b=(b1, b2, …, bm). Задана та же матрица А, элемент которой aij определяет расход i-го ингридиента для производства j-го изделия. Кроме того задан вектор цен p=(p1, p2, …, pn) на продукцию предприятия. Требуется отыскать вектор цен ингридиентов u=(u1, u2, …, um), где ui - цена единицы i-го ингридиента (i=1, …,m), чтобы выполнялись условия:
| a11u1 + a21u2 + … + am1um ³ p1 | ||
| ||
| …………………………….……………………. | ||
| a1nu1 + a2nu2 + … + amnum ³ pn | ||
| ui ³ 0, (i=1,…,m) |
при достижении минимума целевой функции
|
W=b1u1 + … + bmum
j-ое условие (2) означает, что стоимость всех ингридиентов, идущ на производство j-го изделия, не меньше рыночной цены этого изделия.
Условие несвободности uj³0 означает, что j-й ингредиент либо бесплатен (uj=0), либо стоит положительное количество рублей (uj >0).
Опорным решением задачи (1)-(1') называется точка множества W, в которой не менее чем n ограничений из (1) обращается в верное равенство. Это - так называемая, угловая точка множества. Для n=2 это - вершина плоского угла.
Опорным решением задачи (2)-(2') называется точка, в которой не менее чем m ограничений из (2) обращается в верное равенство.
В задаче (1)-(1') опорное решение - точка х=(0,…,0), начало координат. В задаче (2)-(2') начало координат - точка u=(0,…,0), опорным решением не является.
Опорное решение, доставляющее максимум функции (1') или минимум функции (2') называется оптимальным. В работе [1] показано, что оптимальное решение можно всегда искать среди опорных решений.
Среди линейных ограничений задачи (1)-(1') кроме неравенств могут быть и равенства. Тогда условимся писать эти равенства первыми. Если их количество равно k, то область W запишется в виде:
| a11x1 + a12x2 + … + a1nxn = b1 | ||
| …………………………….……………………… | ||
| ||
| ak+1, 1x1+ak+1, 2x2+…+ak+1, n xn£bk+1 | ||
| …………………………….……………………… | ||
| am1x1 + am2x2 + … + amnxn £ bm | ||
| xj ³ 0, (j=1,…,n) |
Требуется найти максимум функции
|
Z=p1x1 + p2x2 + … + pnxn
В общем случае среди переменных xj могут быть свободные. Номера свободных переменных будем хранить в отдельном массиве.
При формировании двойственной задачи к задаче (3)-(3') i-му ограничению - равенству будет соответствовать свободная переменная ui (i=1,…,k), а свободной переменной xj ограничение - равенство:
a1j u1 + a2j u2 + … + amj um =pj
Введем вспомогательные переменные yi³0 (i=1,…,n) и запишем ограничения (3) и функцию Z в виде:
| 0 = a11 (-x1) + a12 (-x2) + … + a1n (-xn) + a1, n+1 | ||
| …………………………………………………….……………………………………… | ||
| ||
| yk+1 = ak+1, 1 (-x1) + ak+1, 2(-x2)+ … + ak+1, n(-xn) + ak+1, n+1 | ||
| …………………………………………………….……………………………………… | ||
| ym = am1 (-x1) + am2 (-x2) + … + amn(-xn) + am, n+1 | ||
| Z= am+1, 1 (-x1) + am+1, 2(-x2)+ … + am+1, n(-xn) + am+1, n+1 |
Условие несвободности отдельных или всех переменных здесь не отмечено. Обозначения:
ai, n+1 = bi (i=1, …, m),
am+1, j = -pj (j=1, …, n)
am+1, n+1 = 0.
Таким образом, матрицу а мы дополнили столбцом свободных членов и строкой коэффициентов целевой функции, изменив знаки этих коэффициентов на противоположные. Тогда задачу (4) можно представить в виде таблицы. 1:
Прямая задача Таблица 1
| -x1 | -x2 | -xn | 1 | ||
| 0 = | a11 | a12 | … | a1n | a1, n+1 |
| …… | …………………………… | ……… | |||
| 0 = | .. | ak, n+1 | |||
| yk+1 = | ak1 | ak2 | … | akn | ak+1, n+1 |
| …… | ak+1, 1 | ak+1, 2 | … | ak+1, n | ……… |
| ym = | …………………………… | ……… | |||
| am1 | am2 | … | amn | am, n+1 | |
| Z = | am+1, n | am+1, 2 | … | am+1, n | am+1, n+1 |
Номера свободных переменных запоминаются отдельно.
Совместим таблицу двойственной задачи с таблицей. 1 и получим таблицу. 2.
Прямая и двойственная задачи Таблица 2
| v1 = | v2 = | vn = | W = | |||
| -x1 | -x2 | -xn | 1 | |||
| u1 | 0 = | a11 | a12 | … | a1n | a1, n+1 |
| …… | ……………...……………… | ……… | ||||
| uk | 0 = | ak1 | ak2 | … | akn | ak, n+1 |
| uk+1 | yk+1 = | ak+1, 1 | ak+1, 2 | … | ak+1, n | ak+1, n+1 |
| …… | …………………………… | ……… | ||||
| um | ym = | am1 | am2 | … | amn | am, n+1 |
| 1 | Z = | am+1, n | am+1, 2 | … | am+1, n | am+1, n+1 |
vj - вспомогательные переменные двойственной задачи.
Тогда j-е ограничение из таблицы имеет вид:
vj = a1j u1 + a2j u2 + … + amj um + am+1, j ³ 0, если xj ³ 0
Если переменная xj свободна, то ей соответствует ограничение-равенство двойственной задачи:
0=a1j u1 + a2j u2 + … + amj um + am+1, j
т.е. вместо vj фактически будет нуль.
Кроме того первые k переменных двойственной задачи свободны, а остальные несвободны.
Целевая функция двойственной задачи
W= a1, n+1 u1 + a2, n+1 u2 + … + am, n+1 um + am+1, n+1
Совмещение в одной таблице прямой и двойственной задачи неслучайно. Решая прямую задачу, мы получаем о дновременно решение двойственной задачи, причем
max Z = min W = am+1, n+1
Сделаем замену переменных в таблице 1 , перебросив вспомогательную переменную yr на верх таблицы со знаком минус, а основную пременную xs на бок таблицы (ars¹0). Это означает движение из вершины x=(0, …, 0) в другую вершину многогранника W по его ребру. Элемент аrs называется разрешающим, строка r - разрешающей строкой, столбец s - разрешающим столбцом. Такая замена переменных носит название модифицированных жордановых исключений (МЖИ). Элементы матрицы а, не принадлежащие разрешающему столбцу или разрешающей строке, назовем рядовыми.
2.2 Описание исходных данных и результатов решения задачи линейного программирования.
Обсудим исходные данные (текстовой файл simp.dat) и результаты решения задачи линейного программирования (текстовой файл simp.res). В начале файла simp.dat расположены, так называемые, представительские данные - строковые данные, каждое из которых распологается в файле с новой строки:
1. Строка с номером варианта,
2. Строка с русским названием модуля,
3. Строка с координатами студента (ФИО, факультет, курс, группа),
4. Строка с датой исполнения.
Далее следуют строки файла с числовыми исходными данными:
1. Управляющий вектор kl - отдельная строка состоящая из трёх чисел kl1 , kl2 , kl3:
kl1=0, если необходимо получить решение только прямой задачи.
kl1=1, если необходимо получить решение только двойственной задачи.
kl1=2, если необходимо получить решение обеих задач.
kl2=0, если нет свободных переменных, иначе kl2 равен числу этих нуль-уравнений.
2. Число ограничений и переменных (отдельная строка ввода).
3. Коэффициенты расширенной матрицы a, начиная с отдельной строки ввода.
4. Вектор номеров свободных переменных, если они есть, начиная с отдельной строки ввода.
Результаты решения зависят от значения kl .
Если kl1=0, то при благоприятном исходе это будет вектор оптимального решения прямой задачи и оптимальное значение целевой функции. При неблагоприятном исходе, это одно из сообщений: либо "Система ограничений несовместна", либо "Целевая функция неограничена".
Если kl2=1, то же для двойственной задачи.
Если kl2=2, то сначала выдается решение прямой, а потом двойственной задачи. При не благоприятном исходе сообщения справедливы только для прямой задачи (для двойственной аналогичные сообщения не выдаются). Результаты помещаются в файл simp.res.
Похожие работы
... [a,b]. Теперь мы можем рассматривать функции в произвольных нормированных пространствах. III. Методы аппроксимации 3.1 Приближение функций многочленами. Алгебраическим многочленом степени n называется функция - действительные числа, называемые коэффициентами. Алгебраические многочлены являются простейшими функциями. Они непрерывны при любом x. Производная многочлена- так же многочлен, степень ...
... u(x1, x2) в пяти точках сетки, а именно в точках (x1i, x2j), (x1i± 1, x2j), (x1i, x2 j± 1). Указанное множество точек называется шаблоном разностного оператора. Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих большее число точек. 2. Исследование аппроксимации и сходимости 2.1. Аппроксимация дифференциального уравнения. Ранее рассматривалась краевая задача (k(x) ...
... PRINT X, Y NEXT X END XC= 10 Х Y 1.3 -6.56 5.4 -3.77 9.5 -1.84 13.6 .1 17.7 2.29 21.8 4.31 25.9 5.86 30 8.82 34.1 11.33 38.2 11.27 S=-1.594203 АППРОКСИМАЦИЯ ФУНКЦИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. В инженерной деятельности часто ...
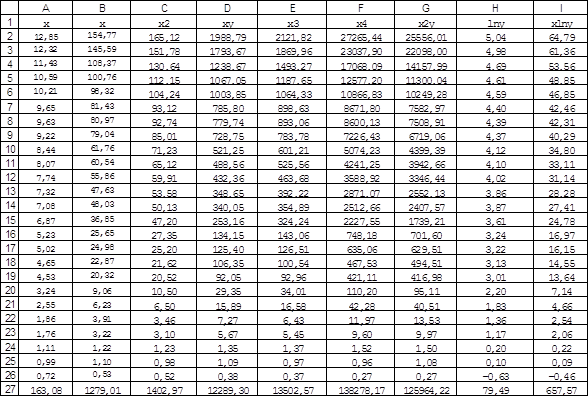
... считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные. 3. Расчет коэффициентов аппроксимации в Microsoft Excel. Вариант №22 Функция y=f(x) задана таблицей 1 Таблица 1 Исходные данные. 12.85 154.77 9.65 81.43 7.74 55.86 5.02 24.98 1.86 3.91 12.32 145.59 9.63 80.97 7.32 ...
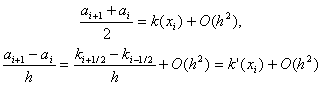
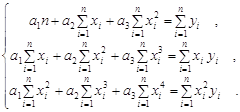
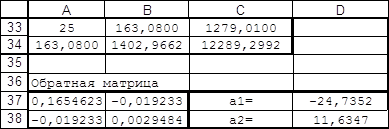
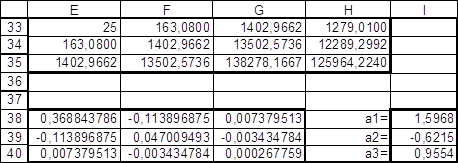
0 комментариев