Навигация
Блок-схема и параметры реализованной процедуры
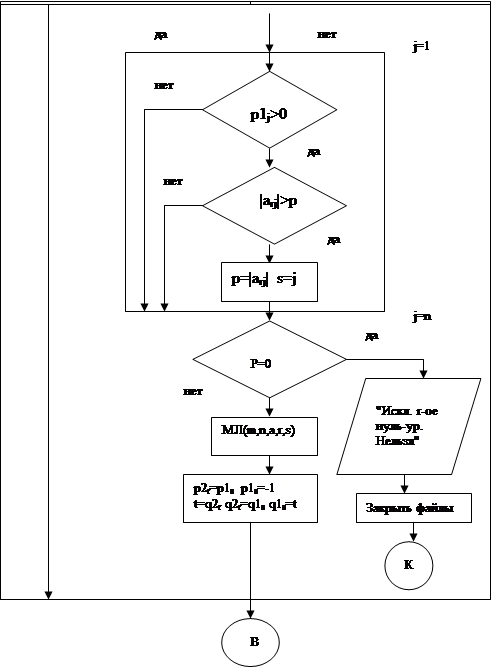
6.2 Блок-схема и параметры реализованной процедуры.
|
 | |||
| |||
Обращащение: isnu(k1,m,n,a,p1,q1,p2,q2). Используются модули typesm, mjim.
Параметры подпрограммы isnu:
| Наименование | Обозначение |
| Число ограничений | m |
| Число переменных | n |
| Матрица задачи | a |
| Отслеживающие векторы | p1, q1, p2, q2 |
В итоге успешной работы алгоритма все нуль-уравнения будут исключены, и в отслеживающем векторе p1 это будет отмечено как -1, что даст возможность в дальнейшем соответствующие столбцы матрицы А при выборе разрешающего элемента не трогать. Если же алгоритм применить нельзя, то будет выдано сообщение (см. блок-схему), и работа программы закончится.
7.2 Листинг модуля, исходных данных и результатов машинного расчета.
unit isnum;
interface
uses typesm,mjim;
procedure isnu(var k1:k1t;m,n:integer; var a:at;
var p1,q1:vec1it; var p2,q2:vec2it);
implementation
procedure isnu;
var p:real;k,s,r,j,t:integer;
begin
for r:=1 to k do begin
if p2[r]<0 then p1[abs(p2[r])]:=-1;end;
p:=0;
for j:=1 to n do begin
if p1[j]>0 then begin
if abs(a[r,j])>p then begin p:=abs(a[r,j]);s:=j;end;
end;end;
if p=0 then begin writeln(fo,'Исключить r',r:6,'-ое нуль-уравнение нельзя');
close(fi);close(fo);halt end;
mji(m,n,a,r,s);
p2[r]:=p1[s];p1[s]:=-1;
t:=q2[r];q2[r]:=q1[s];q1[s]:=t;
end;
end.
Исходный файл simp.dat:
12
Исключение нуль-уравнений
Моносов ЭОУС-1-2 преподаватель Марьямов А. Г.
12.05.98
2 2 0
5 3
-2 -1 1 -2
1 -1 0 -1
-1 -1 0 -2
0 1 0 2
2 1 0 4
4 4 0 0
1 2
Файл результатов simp.res:
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА ИНФОРМАТИКИ И ПРИКЛАДНОЙ МАТЕМАТИКИ
Лабораторная работа по информатике
Факультет ЭОУС, 2-ой семестр обучения
Решение задачи линейного программирования
Вариант 12
модуль: Исключение нуль-уравнений
Исполнил студент Моносов ЭОУС-1-2 преподаватель Марьямов А. Г.
Дата исполнения: 12.05.98
Управляющий вектор:
2 2 0
Число ограничений: 5
Число переменных: 3
Матрица задачи
Н-р Коэффициенты Св. члены
строки
1 -2.00000 -1.00000 1.00000 -2.00000
2 1.00000 -1.00000 0.00000 -1.00000
3 -1.00000 -1.00000 0.00000 -2.00000
4 0.00000 1.00000 0.00000 2.00000
5 2.00000 1.00000 0.00000 4.00000
6 4.00000 4.00000 0.00000 0.00000
Вектор номеров свободных переменных:
1 2
Вектор решения прямой задачи:
1.00000 2.00000 3.00000
Значение целевой функции прямой задачи= 12.00000
Вектор решения двойственной задачи:
0.00000 4.00000 0.00000 8.00000 0.00000
Значение целевой функции двойственной задачи= 12.00000
8.2 Ручной расчет задачи линейного программирования.
Требуется максимизировать функцию
z=4x1+5x2
при ограничениях:
-2x1-x2+x3=-2
x1-x2£ -1
- x1 - x2 £ -2
0x1+ 1x2 £ 2
2x1 + 1x2 £ 4
x3 ³ 0
Коэфициенты ограничений, записанных в таком виде, переписываются со своими знаками, в последней строке таблицы записываются коэффициенты целевой функции с противоположными знаками. Сперва следует исключить свободные переменные, перекинув их на бок таблицы:
| -x1 | -x2 | -x3 | 1 | |
| 0= | -2 | -1 | 1 | -2 |
| y2= | 1 | -1 | 0 | -1 |
| y3= | -1 | -1 | 0 | -2 |
| y4= | 0 | 1 | 0 | 2 |
| y5= | 2 | 1 | 0 | 4 |
| z= | -4 | -4 | 0 | 0 |
| -x1 | -y4 | -x3 | 1 | |
| 0= | -2 | 1 | 1 | 0 |
| y2= | 1 | 1 | 0 | 1 |
| y3= | -1 | 1 | 0 | 0 |
| *x2= | 0 | 1 | 0 | 2 |
| y5= | 2 | -1 | 0 | 2 |
| z= | -4 | 4 | 0 | 8 |
| -y2 | -y4 | -x3 | 1 | |
| 0= | -2 | 3 | 1 | 2 |
| *x1= | 1 | 1 | 0 | 1 |
| y3= | -1 | 2 | 0 | 0 |
| *x2= | 0 | 1 | 0 | 2 |
| y5= | 2 | -3 | 0 | 0 |
| z= | 4 | 8 | 0 | 12 |
После этого следует исключить нуль-уравнение:
| * | ||||
| -y2 | -y4 | -y1 | 1 | |
| x3= | -2 | 3 | 1 | 2 |
| *x1= | 1 | 1 | 0 | 1 |
| y3= | -1 | 2 | 0 | 0 |
| *x2= | 0 | 1 | 0 | 2 |
| y5= | 2 | -3 | 0 | 0 |
| z= | 4 | 8 | 0 | 12 |
Мы видим, что свободные члены в непомеченных строках неотрицательны, следовательно опорное решение получено и надо перейти к поиску оптимального решения. Находим непомеченные столбцы с отрицательными коэфициентами целевой функции, исключая последний. У нас таких нет, поэтому оптимальное решение получено и переходим к извлечению результатов. Для этого составим еще одну таблицу, где содержаться переменные прямой и двойственной задач. Для извлечения решений нужны только столбец свободных членов и строка коэффициентов целевой функции. Поэтому внутренняя часть таблицы не преведена.
| u2= | u4= | u1= | w= | ||
| -y2 | -y4 | -y1 | 1 | ||
| v3= | x3= | -2 | 3 | 1 | 2 |
| v1= | x1= | 1 | 1 | 0 | 1 |
| u3= | y3= | -1 | 2 | 0 | 0 |
| v2= | x2= | 0 | 1 | 0 | 2 |
| u5= | y5= | 2 | -3 | 0 | 0 |
| 1 | z= | 4 | 8 | 0 | 12 |
В итоге получаем следующие результаты:
1. Прямая задача. Переменные прямой задачи, находящиеся сверху таблицы равны в решении 0, а сбоку - соответствующим свободным членам:
x1=1; x2=2; x3=2.
2. Двойственная задача. Переменные двойственной задачи, находящиеся сверху таблицы равны 0, а сбоку - соответствующим коэфициентам целевой функции:
u1=0; u2=4; u3=0; u4=8; u5=0.
Значение целевых функций обеих задач zmax= wmin=12.
9.2 Выводы.
Полученные результаты при ручном расчёте совпадают с данными машинного счёта. Это подтверждает правильность составления алгоритма и написания программы.
Список использованной литературы.
· Турчак Л. И. "Основы численных методов".
· Марьямов А. Г. "Применение модульного способа програмирования в среде Turbo Pascal 7.0 с целью решения полной задачи линейного программирования".
Похожие работы
... [a,b]. Теперь мы можем рассматривать функции в произвольных нормированных пространствах. III. Методы аппроксимации 3.1 Приближение функций многочленами. Алгебраическим многочленом степени n называется функция - действительные числа, называемые коэффициентами. Алгебраические многочлены являются простейшими функциями. Они непрерывны при любом x. Производная многочлена- так же многочлен, степень ...
... u(x1, x2) в пяти точках сетки, а именно в точках (x1i, x2j), (x1i± 1, x2j), (x1i, x2 j± 1). Указанное множество точек называется шаблоном разностного оператора. Возможны разностные аппроксимации оператора Лапласа и на шаблонах, содержащих большее число точек. 2. Исследование аппроксимации и сходимости 2.1. Аппроксимация дифференциального уравнения. Ранее рассматривалась краевая задача (k(x) ...
... PRINT X, Y NEXT X END XC= 10 Х Y 1.3 -6.56 5.4 -3.77 9.5 -1.84 13.6 .1 17.7 2.29 21.8 4.31 25.9 5.86 30 8.82 34.1 11.33 38.2 11.27 S=-1.594203 АППРОКСИМАЦИЯ ФУНКЦИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ. В инженерной деятельности часто ...
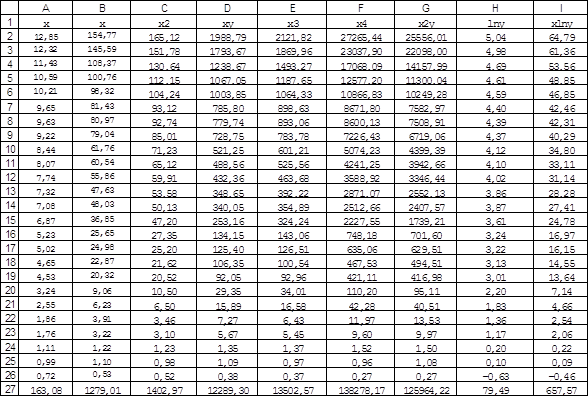
... считать, что построенная эмпирическая формула наиболее точно отражает эмпирические данные. 3. Расчет коэффициентов аппроксимации в Microsoft Excel. Вариант №22 Функция y=f(x) задана таблицей 1 Таблица 1 Исходные данные. 12.85 154.77 9.65 81.43 7.74 55.86 5.02 24.98 1.86 3.91 12.32 145.59 9.63 80.97 7.32 ...
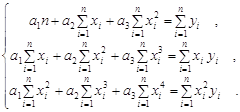
0 комментариев