Навигация
1.3 Векторная графика
Как в растровой графике основным элементом изображения является точка, так в векторной графике основным элементом изображения является линия, при этом не важно, прямая это линия или кривая.
В растровой графике тоже существуют линии, но там они рассматриваются как комбинации точек. Для каждой точки линии в растровой графике отводится одна или несколько ячеек памяти (чем больше цветов могут иметь точки, тем больше ячеек им выделяется). Соответственно, чем длиннее растровая линия, тем больше памяти она занимает. В векторной графике объем памяти, занимаемый линией, не зависит от размеров линии, поскольку линия представляется в виде формулы, а точнее говоря, в виде нескольких параметров. Чтобы ни делали с этой линией, меняются только ее параметры, хранящиеся в ячейках памяти. Количество же ячеек остается неизменным для любой линии.
Линия - это элементарный объект векторной графики. Все, что есть в векторной иллюстрации, состоит из линий. Простейшие объекты объединяются в более сложные, например, объект четырехугольник можно рассматривать как четыре связанные линии, а объект куб еще более сложен: его можно рассматривать либо как двенадцать связанных линий, либо как шесть связанных четырехугольников. Из-за такого подхода векторную графику часто называют объектно-ориентированной графикой.
Объекты векторной графики хранятся в памяти в виде набора параметров, но надо помнить о том, что на экран все изображения все равно выводятся в виде точек. Перед выводом на экран каждого объекта программа производит вычисления координат экранных точек в изобра жении объекта, поэтому векторную графику иногда называют вычисляемой графикой. Аналогичные вычисления производятся и при выводе объектов на принтер.
Как и все объекты, линии имеют свойства. К этим свойствам относятся: форма линии, ее толщина, цвет, характер линии (сплошная, пунктирная и т.п.). Замкнутые линии имеют свойство заполнения. Внутренняя область замкнутого контура может быть заполнена цветом, текстурой, картой. Простейшая линия, если она не замкнута, имеет две вершины, которые называются узлами. Узлы тоже имеют свойства, от которых зависит, как выглядит вершина линии и как две линии сопрягаются между собой.
1.4 Алгоритмы вычерчивания отрезков
Поскольку экран растрового дисплея с электронно-лучевой трубкой (ЭЛТ) можно рассматривать как матрицу дискретных элементов (пикселов), каждый из которых может быть подсвечен, нельзя непосредственно провести отрезок из одной точки в другую. Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением в растр. В сочетании с процессом построчной визуализации изображения он известен как преобразование растровой развертки. Для горизонтальных, вертикальных и наклоненных под углом 45° отрезков выбор растровых элементов очевиден. При любой другой ориентации выбрать нужные пикселы труднее, что показано на рис. 1.1.
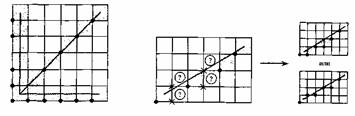
Рис. 1.1 Разложение в растр отрезков прямых
Прежде чем приступать к обсуждению конкретных алгоритмов рисования отрезков, полезно рассмотреть общие требования к таким алгоритмам и определить желаемые характеристики изображения. Очевидно, что отрезки должны выглядеть прямыми, начинаться и заканчиваться в заданных точках. Яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона. Наконец, рисовать нужно быстро. Как это часто бывает, не все из перечисленных критериев могут быть полностью удовлетворены. Сама природа растрового дисплея исключает генерацию абсолютно прямых линий (кроме ряда специальных случаев), равно как и точное совпадение начала и конца отрезка с заданными точками. Тем не менее при достаточно высоком разрешении дисплея можно получить приемлемое изображение.
Постоянная вдоль всего отрезка яркость достигается лишь при проведении горизонтальных, вертикальных и наклоненных под углом 45 ° прямых. Для всех других ориентации разложение в растр приведет к неравномерной яркости, как это показано на рис. 2.1. Даже для частных случаев яркость зависит от наклона: заметим, например, что расстояние между центрами соседних пикселов для отрезка под углом 45° больше, чем для вертикальных и горизонтальных прямых. Поэтому вертикальные и горизонтальные отрезки будут выглядеть ярче, чем наклонные. Обеспечение одинаковой яркости вдоль отрезков разных длин и ориентации требует извлечения квадратного корня, а это замедлит вычисления. Обычным компромиссом является нахождение приближенной длины отрезка, сведение вычислений к минимуму, предпочтительное использование целой арифметики, а также реализация алгоритмов на аппаратном или микропрограммном уровне.
2 Алгоритмы генерации отрезков
2.1 Цифровой Дифференциальный анализатор
Один из методов разложения отрезка в растр состоит в решении дифференциального уравнения, описывающего этот процесс. Для прямой линии имеем
![]()
Решение представляется в виде
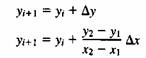
где x1, y1 и x2, y2 - концы разлагаемого отрезка и yi - начальное значение для очередного шага вдоль отрезка. Фактически уравнение [1] представляет собой рекурентное соотношение для последовательных значений y вдоль нужного отрезка. Этот метод, используемый для разложения в растр отрезков, называется цифровым дифференциальным анализатором (ЦДА). Впростом ЦДА либо Dx, либо Dy (большее из приращений) выбирается в качестве единицы растра. Ниже приводится простой алгоритм, работающий во всех квадрантах:
Процедура разложения в растр отрезка по методу цифрового дифференциального анализатора (ЦДА)
предполагается, что концы отрезка (x1, y1) и (x2, y2) не совпадают
Integer - функция преобразования вещественного числа в целое.
Sign - функция, возвращающая -1, 0, 1 для отрицательного, нулевого и положительного аргумента соответственно
аппроксимируем длину отрезка
if abs(x2 - x1) >= abs(y2 - y1) then
Длина = abs(x2 - x1) else
Длина = abs(y2 - y1) end
полагаем большее из приращений x или y равными единице растра
x = (x2 - x1) // Длина
y = (y2 - y1) // Длина
округляем величины, а не отбрасываем дробную часть
использование знаковой функции делает алгоритм пригодным для всех квадрантов
x = x1 + 0.5 * Sign(x)
y = y1 + 0.5 * Sign(y)
начало основного цикла
i =1
while (i <= Длина)
вывод точки PutPixel (Integer(x), Integer(y))
x = x + x
y = y + y
i = i + 1
end
Похожие работы
... подход к разработке эффективного алгоритма для решения любой задачи – изучить ее сущность. Довольно часто задачу можно сформулировать на языке теории множеств, относящейся к фундаментальным разделам математики. В этом случае алгоритм ее решения можно изложить в терминах основных операций над множествами. К таким задачам относятся и задачи информационного поиска, в которых решаются проблемы, ...
... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...
... , что затрудняет построение научно обоснованной методики формирования монологической формы речи. 1.3 Психолого-педагогические условия формирования образно-выразительных средств речи у дошкольников с ОНР (III уровень) в процессе обучения монологическому высказыванию Детям с речевым недоразвитием свойственны ослабление и нарушение коммуникативных отношений речи к неречевым структурам на ...
... области психологической науки – психологии компьютеризации. Ее предмет – порождение, функционирование и структура психологического отражения в процессе деятельности, связанной с содержанием и использованием компьютерной техники и ее программного обеспечения. Роль компьютера в учебном процессе абсолютизируется, подчас высказывается мнение, что компьютер может полностью заменить учителя, и что ...




0 комментариев