Алгоритм Брезенхема

2.2 Алгоритм Брезенхема

В 1965 году Брезенхеймом был предложен простой целочисленный алгоритм для растрового построения отрезка. Алгоритм выбирает оптимальные растровые координаты для представления отрезка. В процессе работы одна из координат — либо x, либо у (в зависимости от углового коэффициента) — изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между действительным положением отрезка и ближайшими координатами сетки. Такое расстояние мы назовем ошибкой.

Алгоритм построен так, что требуется проверять лишь знак этой ошибки. На рис. 1.2 это иллюстрируется для отрезка в первом октанте, т. е. для отрезка с угловым коэффициентом, лежащим в диапазоне от нуля до единицы. Из рисунка можно заметить, что если угловой коэффициент отрезка из точки (0, 0) больше чем 1/2, то его пересечение с прямой х = 1 будет расположено ближе к прямой у = 1, чем к прямой у = 0. Следовательно, точка растра (1, 1) лучше аппроксимирует ход отрезка, чем точка (1, 0). Если угловой коэффициент меньше 1/2, то верно обратное. Для углового коэффициента,

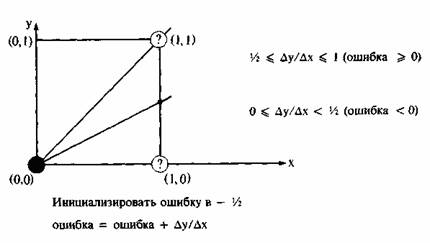
Рис. 1.2 Основная идея алгоритма Брезенхема

равного 1/2, нет какого-либо предпочтительного выбора. В данном случае алгоритм выбирает точку (1, 1).

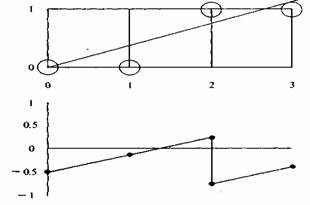
Рис. 1.3 График ошибки в алгоритме Брезенхема

Не все отрезки проходят через точки растра. Подобная ситуация иллюстрируется рис. 1.3, где отрезок с тангенсом угла наклона 3/8 сначала проходит через точку растра (0, 0) и последовательно пересекает три пиксела. Также иллюстрируется вычисление ошибки при представлении отрезка дискретными пикселами. Так как желательно проверять только знак ошибки, то она первоначально устанавливается равной —1/2. Таким образом, если угловой коэффициент отрезка больше или равен 1/2, то величина ошибки в следующей точке растра с координатами (1,0) может быть вычислена как

е = е + m

где m — угловой коэффициент. В нашем случае при начальном значении ошибки —1/2

е = -1/2+ 3/8 = -1/8

Так как е отрицательно, отрезок пройдет ниже середины пиксела. Следовательно, пиксел на том же самом горизонтальном уровне лучше аппроксимирует положение отрезка, поэтому у не увеличивается. Аналогично вычисляем ошибку

е = -1/8 + 3/8 = 1/4

в следующей точке растра (2, 0). Теперь е положительно, а значит, отрезок пройдет выше средней точки. Растровый элемент (2, 1) со следующей по величине координатой у лучше аппроксимирует положение отрезка. Следовательно, у увеличивается на единицу. Прежде чем рассматривать следующий пиксел, необходимо откорректировать ошибку вычитанием из нее единицы. Имеем

е = 1/4- 1 = -3/4

Заметим, что пересечение вертикальной прямой х = 2 с заданным отрезком лежит на 1/4 ниже прямой y = 1. Если же перенести отрезок 1/2 вниз, мы получим как раз величину -3/4. Продолжение вычислений для следующего пиксела дает

e = - 3/4 + 3/8 = - 3/8

Так как e отрицательно, то .у не увеличивается. Из всего сказанного следует, что ошибка — это интервал, отсекаемый по оси у рассматриваемым отрезком в каждом растровом элементе (относительно —1/2).

3. Описание программы

3.1. Описание интерфейса

Реализация каждого метода генерации отрезков проводилась в среде объектно-ориентированного программирования Delphi 7. Поставлена задача запрограммировать алгоритмы генерации отрезков, создать форму для ввода данных и вывода результата.

Для каждого из трех алгоритмов создается окно приложения (рис. 1.4).

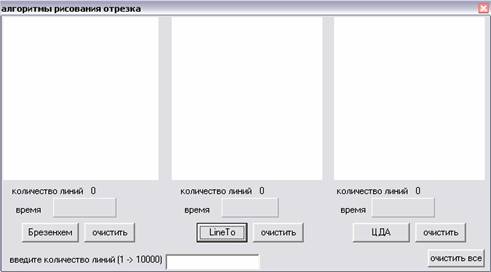
Рис. 1.4. Внешний вид окна приложения

В итоге создано приложение Windows.

На форме расположены:

Три поля, на которых будет отображаться результат построения отрезков для каждого метода в отдельности.

Поле «Ввод количества линий» служит для ввода количества линий, которые будут сгенерированы генератором случайных чисел.

Три поля «время», на которых отображается время построения отрезков для каждого метода в отдельности.

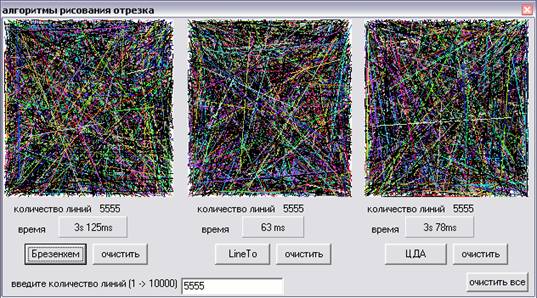
Рис.3.2 Результат работы приложения

3.2. Описание логической структуры

В проект добавлены компоненты Form1 – главная форма. На главной форме размещаются компоненты: Image – окно для вывода линий, Panel – панель для вывода времени, затраченного на генерацию отрезков, Edit1 – окошечко для ввода количества линий, которые будут сгенерированы генератором случайных чисел и Button – кнопка для подтверждения ввода количества линий / для очистки компонента Image и сброса всех настроек. Label – показывает число построенных линий

Заключение

Заканчивая наш обзор методов генерации отрезков, попытаемся сравнить их эффективность.

Метод Брезенхема определенно наихудший из всех сравниваемых, этот алгоритм обладает очень плохими временными характеристиками. Он имеет только учебно-исторический интерес и не может быть рекомендован для практического использования.

Алогритм Цифрового Дифференциального Анализатора в среднем (в зависимости от количества введенных линий) лучше, чем метод Брезенхема. По сравнению с методом Брезенхема метод ЦДА в большинстве случаев может оказаться более быстрым.

Процедура LineTo оказалась самой быстрой и результативной из всех трех алгоритмов

В данной работе рассмотрены некоторые простые и улучшенные методы генерации отрезков: Брезенхема, Цифрового Дифференциального Анализатора и стандартной процедуры LineTo. Мы оценили сложность этих алгоритмов генерации. Алгоритмы этих методов представлены в виде программ. Так же была проанализирована скорость, эффективность использования того или иного вида генерации отрезков.

Целью данной курсовой работы было исследование и сравнение трех наиболее эффективных алгоритмов генерации отрезков: Брезенхема, Цифрового Дифференциального Анализатора и стандартной процедуры LineTo. Поставленная цель была достигнута.

Список литературы

П.В.Вельтмандер "Машинная графика" Издательский дом «Вильямс», 2000.

информация с сайта http://alglib.sources.ru

информация с сайта http://joinbiz.ru

информация с сайта http://kladovka.net.ru

информация с сайта http://Mini-Soft.ru

Приложение

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,

Dialogs,Math, StdCtrls, ExtCtrls, Menus, ToolWin, ComCtrls, ExtDlgs,

ImgList;

type

TPointDrawer = procedure(X, Y: Integer) of object;

TForm1 = class(TForm)

Button1: TButton;

Button2: TButton;

Button3: TButton;

Image1: TImage;

Image2: TImage;

Edit1: TEdit;

Label1: TLabel;

Label2: TLabel;

Label3: TLabel;

Label4: TLabel;

Label5: TLabel;

Button4: TButton;

Button7: TButton;

Image3: TImage;

Button8: TButton;

Button9: TButton;

Label6: TLabel;

Label7: TLabel;

Panel1: TPanel;

Panel2: TPanel;

Panel3: TPanel;

Label8: TLabel;

Label9: TLabel;

Label10: TLabel;

procedure Button1Click(Sender: TObject);

procedure Button2Click(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure Button3Click(Sender: TObject);

procedure Button4Click(Sender: TObject);

procedure Button7Click(Sender: TObject);

procedure Button8Click(Sender: TObject);

procedure Button9Click(Sender: TObject);

private

s:string;

{ Private declarations }

public

{ Public declarations }

end;

var

Form1: TForm1;

time,tm1,tm2:integer;

implementation

//функция вычисления модуля числа

function AbsInt(Value: Integer): Integer;

begin

if Value >= 0 then

Result := Value

else

Result := - Value;

end;

//Цифровой Дифференциальный анализатор

procedure DDA(x1,y1,x2,y2:integer);

var dx,dy,sx,sy,d,d1,d2,x,y,i:integer;

T:tColor;

begin

randomize;

t:=random($7FFFFFFF);

dx:=abs(x2-x1);

dy:=abs(y2-y1);

if x2>=x1 then sx:=1 else sx:=-1;

if y2>=y1 then sy:=1 else sy:=-1;

if dy<=dx then

begin

d:=2*dy -dx;

d1:=2*dy;

d2:=2*(dy-dx);

Form1.Image3.Canvas.Pixels[x1,y1]:=t;

x:=x1+sx;

y:=y1;

for i:=1 to dx do

begin

if d>0 then

begin

d:=d+d2;

y:=y+sy;

end else d:=d+d1;

Form1.Image3.Canvas.Pixels[x,y]:=t;

x:=x+sx;

end;

end else

begin

d:=2*dx-dy;

d1:=2*dx;

d2:=2*(dx-dy);

Form1.Image3.Canvas.Pixels[x1,y1]:=t;

x:=x1;

y:=y1+sy;

for i:=1 to dy do

begin

if d>0 then

begin

d:=d+d2;

x:=x+sx;

end else d:=d+d1;

Form1.Image3.Canvas.Pixels[x,y]:=t;

y:=y+sy;

end;

end;

end;

//описание метода Брезенхема

procedure Bresenham(x1:Integer;y1:Integer;x2:Integer;y2:Integer);

var

x,y,dx,dy,sx,sy,z,e,i: Integer;

Ch : Boolean;

T:tColor;

begin

randomize;

t:=random($7FFFFFFF);

x:=x1;

y:=y1;

dx:=AbsInt(x2-x1); //модуль числа dx

dy:=AbsInt(y2-y1); //модуль числа dy

sx:=Sign(x2-x1);

sy:=Sign(y2-y1);

if (dx=0) and (dy=0) then

begin

form1.image1.Canvas.Pixels[x1,y1]:=t; //вывод точки

Exit;

end;

if dy>dx then

begin

z:=dx; dx:=dy; dy:=z; ch:=True;

end

else ch:=False;

e:=2*dy-dx;

i:=1;

repeat

form1.image1.Canvas.Pixels[x,y]:=t; //вывод точки в цикле

while e>=0 do

begin

if ch then x:=x+sx

else y:=y+sy;

e:=e-2*dx;

end;

if ch then y:=y+sy

else x:=x+sx;

e:=e+2*dy;

i:=i+1;

until i>dx;

end;

{$R *.dfm}

procedure TForm1.Button1Click(Sender: TObject);

var k: integer;

begin

time:=GetTickCount;

label4.Caption:=inttostr(strtoint(label4.Caption)+strtoint(edit1.Text));

for k:=1 to strtoint(Edit1.text) do

Bresenham (random(image1.ClientWidth), random(image1.clientHeight), random (image1.ClientWidth), random(image1.ClientHeight));

time:=GetTickCount-time;

if time>1000 then

begin

tm1:=time mod 1000;

tm2:=time div 1000;

Form1.Panel1.Caption:=IntToStr(tm2)+'s '+IntToStr(tm1)+'ms';

end

else

Form1.Panel1.Caption:=IntToStr(time)+' ms';

end;

procedure TForm1.Button2Click(Sender: TObject);

var m:integer;

begin

time:=GetTickCount;

label5.Caption:=inttostr(strtoint(label5.Caption)+strtoint(edit1.Text));

for m:=1 to strtoint(Edit1.text) do

begin

image2.Canvas.Pen.Color:=random($7FFFFFFF);

image2.Canvas.LineTo(random(image2.ClientWidth),random(image2.ClientHeight));

image2.Canvas.MoveTo(random(image2.ClientWidth),random(image2.ClientHeight));

end;

time:=GetTickCount-time;

if time>1000 then

begin

tm1:=time mod 1000;

tm2:=time div 1000;

Form1.Panel2.Caption:=IntToStr(tm2)+'s '+IntToStr(tm1)+'ms';

end

else

Form1.Panel2.Caption:=IntToStr(time)+' ms';

end;

procedure TForm1.Button8Click(Sender: TObject);

var l:integer;

begin

time:=GetTickCount;

label7.Caption:=inttostr(strtoint(label7.Caption)+strtoint(edit1.Text));

for l:=1 to strtoint(Edit1.text) do DDA

(random(image3.ClientWidth),random(image3.ClientHeight),random(image3.ClientWidth),random(image3.ClientHeight));

time:=GetTickCount-time;

if time>1000 then

begin

tm1:=time mod 1000;

tm2:=time div 1000;

Form1.Panel3.Caption:=IntToStr(tm2)+'s '+IntToStr(tm1)+'ms';

end

else

Form1.Panel3.Caption:=IntToStr(time)+' ms';

end;

procedure TForm1.FormCreate(Sender: TObject);

begin

randomize;

edit1.Text:=inttostr(random(500));

end;

procedure TForm1.Button4Click(Sender: TObject);

begin

form1.image1.Canvas.FillRect(Rect(0,0,ClientWidth,ClientHeight));

form1.Label4.Caption:=inttostr(0);

form1.Panel1.Caption:='';

end;

procedure TForm1.Button7Click(Sender: TObject);

begin

form1.image2.Canvas.FillRect(Rect(0,0,ClientWidth,ClientHeight));

form1.Label5.Caption:=inttostr(0);

form1.Panel2.Caption:='';

end;

procedure TForm1.Button9Click(Sender: TObject);

begin

form1.image3.Canvas.FillRect(Rect(0,0,ClientWidth,ClientHeight));

form1.Label7.Caption:=inttostr(0);

form1.Panel3.Caption:='';

end;

procedure TForm1.Button3Click(Sender: TObject);

begin

Form1.Button7.Click;

Form1.Button4.Click;

Form1.Button9.Click;

end;