Навигация
3.3.1.2 В частотной области
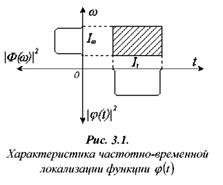
Вейвлет преобразование можно провести в частотной области. Для этого снова в первую очередь необходимо определить материнский вейвлет. Расчет по данной схеме происходит следующим образом: преобразование Фурье самого вейвлета (в данном случае будем рассматривать вейвлет Морле) сконцентрировано вокруг некоторой выделенной частоты w 0 ≠ 0. Поэтому преобразование Фурье вейвлета, растянутого в s раз, будет сконцентрировано вокруг частоты w 0/s (см рис. 4).
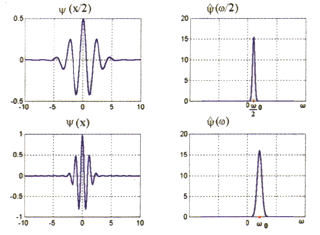
Рис 4. Преобразование Фурье функции вейвлета.
Так как свертка функций эквивалентна их перемножению в частотной области, “строка” s = const на изображении вейвлет преобразования показывает эволюцию изучаемой функции на частотах, близких w 0/s. То есть умножение Фурье-спектра исходной функции на пик в точке w 0/s в частотной области (то есть на Фурье-образ растянутого вейвлета) вырезает из этой функции все то, что дает вклад в ее спектр на частотах, близких w 0/s. В результате получается развертка спектрального компонента во времени. [1]
Основные формулы имеют вид:
где (*) – означает комплексно-сопряженное, а знак (^) – преобразование Фурье.
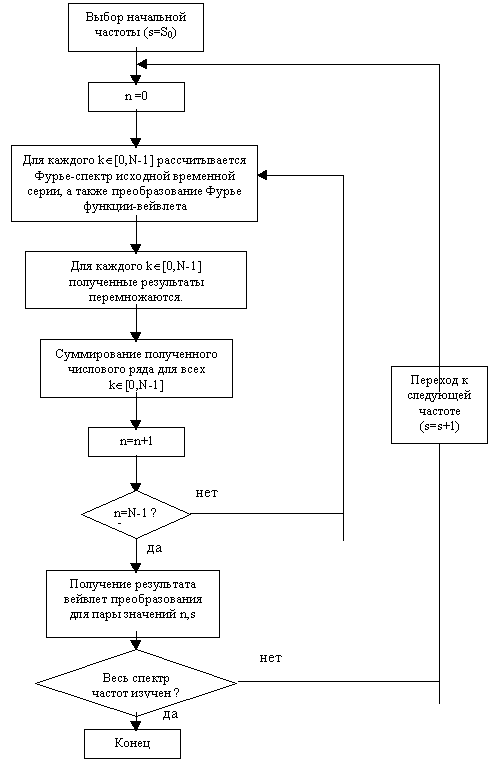
Блок – схема алгоритма:
3.3.2 Выбор материнского вейвлета
В качестве материнского вейвлета подходит любая функция, удовлетворяющая двум вышеуказанным условиям. Для реализации алгоритма в качестве анализирующего вейвлета было решено воспользоваться вейвлетом Морле (рис. 5). Это было сделано по трем причинам:
вейвлет Морле один из наиболее популярных [1] и широко применяется он обладает значительной наглядностью он прост в вычислительном плане, что ускоряет работу алгоритма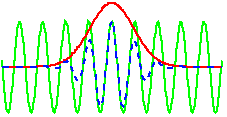
рис 5. Вейвлет Морле.
Фактически вейвлет Морле является произведением комплексной синусоиды на гауссиан.
где y является значением вейвлет функции с безразмерным периодом h , а w 0 - волновой параметр (при реализации w 0=6).
Необходимо также отметить, что вейвлет Морле является комплекснозначным, то есть имеет действительную и мнимую части.
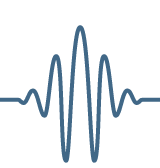
4 ОПРЕДЕЛЕНИЕ УЗЛОВЫХ ТОЧЕК ЭКГ НА ОСНОВЕ НЕПРЕРЫВНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ 4.1 Стандарты описания и обозначения ЭКГ.Электрокардиограмма (ЭКГ) человека – сигнал, считываемый в результате распространения волны деполяризации и реполяризации по сердечной мышце. Электрокардиограмма (ЭКГ) представляет собой некоторый сигнал, имеющий пять характерных пиков - P, Q, R, S и T :
Обозначенные особенности (пики и интервалы) и являются стандартами описания электрокардиограммы человека.
4.2 Постановка задачи идентификации.По временным и амплитудным характеристикам пиков и интервалов врач может определить наличие тех или иных заболеваний у исследуемого пациента. Наиболее важную информацию несет пик R, в частности, именно по этому пику можно найти частоту сердечных сокращений.
В зависимости от конфигурации электродов на теле пациента различают, так называемые, отведения. В медицинской практике используются 12 стандартных отведений, 8 из которых линейно независимы, а еще 4 являются их линейной комбинацией.
В линейных методах для определения временных характеристик ЭКГ (то есть для решения задачи идентификации) обычно используют второе отведение.
Под задачей идентификации, обычно, понимают вычисление временных положений пиков. Также определяют частоты, присутствующие в сигнале, так как, например, присутствие в сигнале определенных высокочастотных компонент может свидетельствовать о ненормальной работе сердца. Поэтому появилась необходимость использования методов частотного анализа, одним из которых является вейвлет-преобразование.
4.3.Построение модели идеальной ЭКГВ медицинских источниках есть сведения о параметрах ЭКГ здорового человека. Обычно эти данные и являются отправной точкой при анализе очередной электрокардиограммы. Для выработки подходов к автоматической идентификации нарушений в работе сердца необходимо построить модель сигнала В результате в ходе выполнения работы были построены две модели идеальной ЭКГ. Первая – для системы Matlab. Вторая – в рамках спецификации компьютерного кардиологического комплекса для анализа ЭКГ человека (для модуля “Vision”). В обоих случаях модель представляет собой одномерный массив чисел, с частотой дискретизации 225 Гц. Длительность выбрана из расчета 2-3 сердечных сокращений.
4.4.Анализ модели ЭКГ.Процедура анализа модели дает представление об эффективности и целесообразности применения соответствующих программных средств и алгоритмов с целью решения той или иной задачи. В связи с этим данному разделу уделено особое внимание.
1. В системе Matlab.
В системе Matlab с использованием стандартных средств данной системы построена модель двух сокращений сердечной мышцы. Графически она имеет следующий вид:
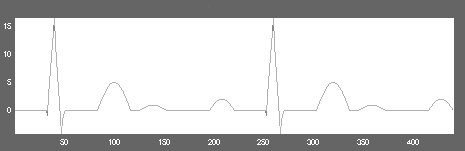
рис 7. Модель ЭКГ в системе Matlab.
Результаты применения аппарата непрерывного вейвлет-преобразования к данной модели выглядят следующим образом:

рис 7. Вейвлет-преобразование в Matlab.
2. С использованием “Vision”.
Модель электрокардиограмы в данном случае имеет те же параметры, однако ее длительность увеличена до 3 секунд. Результаты ее обработки в модуле “Vision” выглядят следующим образом:
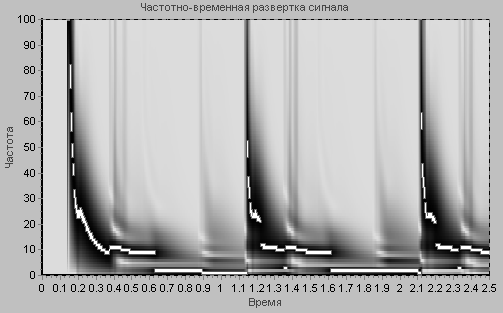
рис 8. Вейвлет-преобразование в “Vision”.
В данном случае темный оттенок свидетельствует о присутствии соответствующей частоты в сигнале в данный момент времени. Частота, в максимальной степени присутствующая в сигнале, выделена особо.
3. Сравнительный анализ полученных результатов.
Результат, полученный в среде Matlab хорошо локализует особенности ЭКГ, однако возникают проблемы с “чтением” масштаба как по временной оси, так и по частотной. Видно, что продвижение по времени осуществляется не по секундам (или другим временным единицам), а по индексу в массиве, содержащим сигнал. О частотных характеристиках сигнала можно судить лишь приблизительно, ввиду их значительной “размазанности” (см приложение 1.). Все это позволяет сделать вывод о том, что аппарат непрерывного вейвлет-преобразования в среде Matlab не слишком эффективен для решения задачи идентификации.
“Vision” дает наглядную частотно-временную развертку, позволяющую быстро и без дополнительных расчетов определить степень присутствия той или иной частоты в конкретный момент времени. Этому в определенной степени способствует удобный масштаб (Гц,Сек). Помощь при решении задачи идентификации оказывает механизм выделения максимально присутствующей частоты (см. рис 8). Неудобство составляют небольшие искажения в области малых времен, связанные с особенностями непрерывного вейвлет-преобразования.
5.ПРОГРАММНАЯ РЕАЛИЗАЦИЯ 5.1.Структура программыПрограмма содержит несколько модулей выполняющих различные функции: описание формата данных, прорисовка “миллиметровки” на которую непосредственно наносится ЭКГ, вычисление непрерывного вейвлет-преобразования, визуализация частотно-временной развертки.
“Vision” читает файлы формата “*.1sf”, содержащие записанную на кардиографе электрокардиограмму. При непосредственном считывании сигнал автоматически отображается в окне на “миллиметровой бумаге”. С помощью полосы скроллинга можно просмотреть все двенадцать отведений. На странице “Анализ” представлены необходимые инструменты для построения частотно-временного спектра. Имеется возможность выбора отведения для анализа (1-12), по умолчанию предлагается второе, как наиболее часто используемое. При проведении анализа измеряется время продолжительности процесса.
5.2.Форматы данныхФормат файла “*.1sf” в начале содержит заголовок, который описывает параметры, а также форму записи электрокардиограммы.
Здесь используется структура имеющая вид:
type
OtvData = array [0..MaxArrayOtv] of SmallInt;
OtvPointer = ^ OtvData;
OtvNumber = array [0..MaxNumberOtv] of OtvPointer;
OtvYLineP = array [0..MaxNumberOtv] of Integer;
PtrOtvYLineP = ^ OtvYLineP;
DataPointer = ^ OtvNumber;
LocationType = (Vertical, Horizontal);
WorkStyleType = (Standart12, Franc, Aculinichev, Reserved);
ECGType = record
Frequency : Word;
Time : Single;
OtvQuantity : Byte;
Location : LocationType;
WorkStyle : WorkStyleType;
MultipleCoef : Single;
end;
Frequency – частота съема ЭКГ, Time – продолжительность съема, OtvQuantity – количество отведений, Location – формат записи (Vertical – предусматривает параллельную запись всех отведений, применяется при считывании данных с кардиографа, Horizontal – последовательная запись отведений: сначала первое, затем второе и т.д.), MultipleCoef – коэффициент числового ряда сигнала.
5.3.Оценка временных затратОсновными критериями, определяющими скорость работы программы являются: частота съема ЭКГ и параметры аппаратной части.
Похожие работы
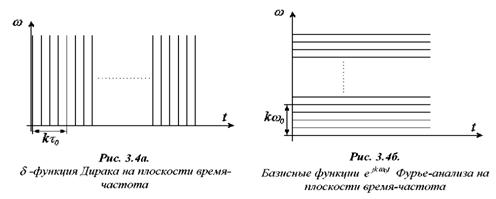
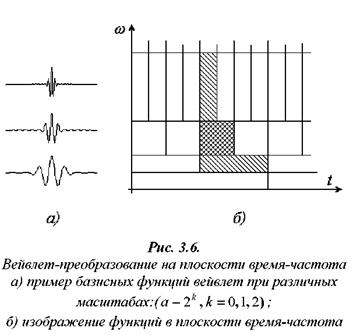
... сохранить относительную "плотность" расположения базисных функций по оси t при расширении или сжатии самой функции и при (рис 3.6) Таким образом, базисные функции для частотно-временного анализа должны обладать следующими свойствами. Ограниченность, т.е. принадлежность L2 . Локализация. Базисные функции вейвлет - анализа, в отличие от преобразования Фурье, должны быть локализованы, т.е. ...
... непосредственно связаны с кратномасштабным анализом сигналов. Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Эти функции могут быть симметричными, асимметричными и несимметричными. Различают вейвлеты с компактной областью определения и не имеющие таковой. Некоторые функции имеют аналитическое выражение, другие – быстрый алгоритм вычисления связанного с ними вейвлет. ...
... плата ввода/вывода. Она необходима для подключения дополнительного оборудования, сбора информации с датчиков и обрабатывание ее. ПРИМЕНЕНИЕ. Системы "машинного зрения" применяются в следующих областях промышленности: · Автомобилестроение. · Электроннике. · Медицинской и фармацевтической. · Машиностроении. · Робототехнике. · ...
... 671 с 7.Короновский А.А., Непрерывный вейвлетный анализ и его приложения / А.А. Короновский, А.Е. Храмов — М. : Физматлит, 2003. — 176 с. </p> <h3>Методические указания</h3> <p> 1. С.Г. Антощук, А.О. Ніколенко Конспект Лекцій по курсу " Методи та засоби комп’ютерних інформаційних технологій" (Електронна версія) , 2005р.</p> <p>2. Методичні рекомендації до ...



0 комментариев