Билеты по математическому анализу

Осн. понятия
Грани числовых мн-в
Числовые последовательности
Непр. ф-ции на пр-ке 1. Осн. понятия

Мат.модель – любой набор кр-ний; неравенств и иных мат. Соотношений, которая в совокупности описывает интересующий нас объект.

Мн-во вещест. чисел разбивается: на рационал. и иррац. Рац. – число, которое можно представить в виде p/q где p и q – цел. числа. Иррац. – всякое вещественное число, которое не явл. рационал.

Любое вещ. число можно представить в виде бесконеч. десят. Дроби а, а1,а2…аn… где а –люб. число, а а1, а2 … аn числа, приним. целые знач.

Некоторые числовые множества.

Мн-ва – первичное понятие, на уровне здравого смысла, его не возможно точно определить.

Для описания мн-в единая символика, а именно, если в мн-во А входят только эл. х, которые обладают некоторым св-вом S(x), то тогда мн-во А описывается А={х½ вып-ся усл S(x)}.

Подмн-ва – если А и В 2 мн-ва и все эл-ты мн-ва А сод-ся в В, то А наз-ся подмн-вом В, А В, если в В сод-ся эл-ты отличные от эл-тов мн-ва А, то В строго шире А, то А наз-ся собственным подмн-вом В. АÌ В. А=В- мн-ва совпадают.

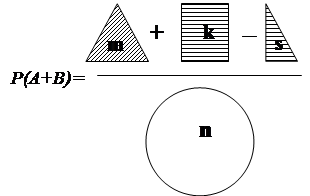
Операции с мн-воми А В={х!х принадл. либо А, либо В} – обьединение мн-в А и В.

АÇ В={х½ хÎ А и хÎ В} пересечение мн-в А и В.

А В={х½ хÎ А, но хÏ В}дополн. к м-ву В во мн-ве А

Числовые мн-ва

R,N,Z,Q - стандартные обозначения мн-в на числ. прямой. (а,в)= {х½ а<х<в} – интервал из R (открытый промежуток, т.к. не содержит границ)

[а,в] – замкнутый промежуток сод. гранич. т-ки.

(а,в] – полуинтервал.

Окрестностью т-ки х наз-ся любой интервал содержащий т-ку х, необязательно симметричную.

2. Грани числовых мн-в

Пусть Х – непустое мн-во веществ. чисел.

Мн-во Х назся огран. сверху(снизу), если сущ-ет число с такое, что для любого х Х вып-ся неравенство с³ х(х³ с). Число с наз-ся верхн.(нижн.) гранью мн-ва Х. Мн-во, огран. сверху и снизу наз-ся ограниченым

Если мн-во имеет 1 верхнюю грань то она имеет их бесчисленное мн-во.

Пример X=R+ - ограничено снизу, но не сверху, значит не ограничено.

Точные грани числовых мн-в

Пусть мн-во Х ограничено сверху, если это мн-во содержит макс число, т.е. наименьшую из своих верхних граней, то это число назся макс мн-ва Х и обозначается Х*=maxX. Если мн-во содержит мин число Х* , то оно min мн-ва Х

Пример Х=[0,1) то max[0,1) не $ . min [0,1)=0

Число Х* наз-ся точной верхн. гранью, мн-ва Х, если во-первых оно явл. верхн. гранью этого мн-ва, а во-вторых при сколь угодном уменьшении Х* получ. число перестает быть верх. гранью мн-ва.

Верхн. грань – supX=x*, а нижн. грань infX=x*

Теорема. Любое непустое ограниченное сверху (снизу) числ. мн-во имеет точную верх(ниж) грань.

Таким образом у огран. мн-ва обе грани $ , док-во основано на непрерывности мн-ва действит. чисел.

3. Числовые последовательности

Если для каждого нат. числа n определено некоторое правило сопоставляющее ему число xn, то мн-во чисел х1,х2, … ,хn, … наз-ся числовой последовательностью и обозначается {xn}, причем числа образующие данную посл-ть наз-ся ее эл-ми, а эл-т хn общим эл-том посл-ти .

!Порядок следования эл-тов оч. важен, перестановка хотя бы 2-х эл-тов приводит к др. посл-ти.

Основные способы задан. посл-ти:

а) явный, когда предъявляется ф-ла позволяющая по заданному n вычислить любой эл-т n, т.е. xn=f(n), где f- некоторая ф-ция нат. эл-та.

б) неявный, при котором задается некоторое рекуррентное отношение и несколько первых членов посл-ти.

Пример:

а) xn=5n x1=5, x2=10

б) x1=-2 xn=4n-1 –3, n=2,3… х2=-11, х3=-47

Ограниченные последовательности(ОП)

Посл-ть {xn} наз-ся огран. сверху(снизу), если найдется какое-нибудь число {xn} M(m) xn£ M " n (xn³ m " n) посл-ть наз-ся огранич., если она огранич. сверху и снизу.

Посл-ть {xn} наз-ся неогранич., если для любого полного числа А сущ-ет эл-т хn этой посл-ти, удовлетворяющий неравенству ½ xn½ >А.

Сходящиеся и расходящиеся посл-ти. Св-ва сходящихся посл-тей. Теорема “Об единственности пределов”. Теорема “Сходящаяся посл-ть ограничена”. Теорема “О сходимости монотон. посл-ти” 4. Сходящиеся и расходящиеся посл-ти

Большое внимание уд-ся выяснению вопроса: обладает ли данная посл-ть сл-щим св-вом (сходимости) при неогранич. Возрастании номеров посл-ти эл-ты посл-ти сколь угодно близко приближаются к некоторому числу а или же этого св-ва нет.

Опр Если для любого e >0 найдется такой номер N, для любого n >N:½ xn-a½ < e

Все посл-ти имеющие предел наз-ся сходящимися, а не имеющее его наз-ся расходящимися.

Связь сходящихся посл-тей и б/м.

Дает сл. теорему

Теорема Для того чтобы посл-ть xn имела пределом число а необходимо, чтобы эл-ты этой посл-ти можно было представить в виде xn=a+a n, где посл-ть {a n}® 0, т.е. является б/м.

Док-во

а) Допустим, что xn® a и укажем посл-ть a n удовл. равенству xn=a+a n. Для этого просто положим a n=xn-a, тогда при n® ¥ ½ xn-a½ равно растоянию от xn до а ® 0 => a n б/м и из равенства преобразования определяю a n получаем xn=a+a n.

Свойство б/м

Если {xn},{yn}- любые посл-ти, то их сумма {xn+yn}, это есть пос-ть с общим членом xn+yn. Аналогично с разностью, частным и умножением.

Т-ма о св-вах б/м

а) {xn}и{yn}-б/м пос-ти, б/м

1) их сумма, разность и произведение являются б/м

2) Произведение любой огранич. посл-ти на б/м являются б/м

!О частном не говорят, т.е. частное б/м может не быть б/м.

Посл-ть {xn} явл. б/б, если для любого числа с>0 сущ-ет номер N для всех номеров n>N ½ xn½ >c.

!Понятие б/б не совпадает с неограниченной: посл-ть может быть неогранич., но не является б/б.

Пример 1,1/2,3,1/4,5,1/6,7… явл. неогранич., т.е. принимает сколь угодно большие по модулю значения, однако в ней имеются эл-ты со сколь угодно большими номерами принимающие дробные знач. и сколь угодно малые по модулю.

Св-ва сходящихся посл-тей Теорема “Об единственности пределов”

Если посл-ть xn сходится, то она имеет единственный предел.

Док-во (от противного)

{xn} имеет два разл. Предела a и b, а¹ b. Тогда согласно определению пределов любая из окрестностей т. а содержит все эл-ты посл-ти xn за исключением конечного числа и аналогичным св-вом обладает любая окрестность в точке b. Возьмем два радиуса e = (b-a)/2, т.к. эти окрестности не пересекаются, то одновременно они не могут содержать все эл-ты начиная с некоторого номера. Получим противоречие теор. док-на.

Теорема “Сходящаяся посл-ть ограничена”

Пусть посл-ть {xn}® а e >о N:" n>N½ xn-a½ <e эквивалентна а-e <xn<a+e " n>N => что каждый из членов посл-ти удовлетворяет неравенству½ xn½ £ c = max {½ a-e ½ ,½ a+e ½ ,½ xn½ ,…,½ xn-1½ }

Теорема “Об арифметических дейсьвиях”

Пусть посл-ть {xn}® a,{yn}® b тогда арифметические операции с этими посл-тями приводят к посл-тям также имеющие пределы, причем:

а) предел lim(n® ¥ )(xn± yn)=a± b

б) предел lim(n® ¥ )(xn* yn)=a* b

в) предел lim(n® ¥ )(xn/yn)=a/b, b¹ 0

Док-во:

а)xn± yn=(а+a n)± (b+b n)=(a± b)+(a n± b n) Правая часть полученная в разности представляет сумму числа a+b б/м посл-тью, поэтому стоящая в левой части xn+yn имеет предел равный a± b. Аналогично др. св-ва.

б) xn* yn=(а+a n)* (b+b n)=ab+a nb+ab n+a nb n

a n* b – это произведение const на б/м

а* b n® 0, a nb n® 0, как произведение б/м.

=> поэтому в правой части стоит сумма числа а* b+ б/м посл-ть. По т-ме О связи сходящихся посл-тей в б/м посл-ти в правой части xn* yn сводится к a* b

Практический вывод состоит в том, что нахожд. пределов посл-тей заданных сл. выражениями можно сводить к более простым задачам вычисления lim от составляющих этого выр-ния

Посл-ть {xn} наз-ся возр., если x1<…<xn<xn+1<…;

неубывающей, если x1£ x2£ …£ xn£ xn+1£ …; убывающей, если x1>x2>…>xn>xn+1>…; невозр., если x1³ x2³ …³ xn³ xn+1³ …

Все такие посл-ти наз-ся монотонными. Возр. и убыв. наз-ся строго монотонными

Монотонные посл-ти ограничены с одной стороны, по крайней мере. Неубывающие ограничены снизу, например 1 членом, а не возрастыющие ограничены сверху.

Теорема “О сходимости монотон. посл-ти”

Всякая монотонная посл-ть явл-ся сходящейся, т.е. имеет пределы.

Док-во Пусть посл-ть {xn} монотонно возр. и ограничена сверху. X – все мн-во чисел которое принимает эл-т этой посл-ти согласно усл. Теоремы это мн-во огранич., поэтому по соотв. Теореме оно имеет конечную точную верх. грань supX xn® supX (обозначим supX через х*). Т.к. х* точная верх. грань, то xn£ x* " n. " e >0 вып-ся нер-во $ xm(пусть m- это n с крышкой):xm>x*-e при " n>m => из указанных 2-х неравенств получаем второе неравенство x*-e £ xn£ x*+e при n>m эквивалентно ½ xn-x*½ <e при n>m. Это означает, что x* явл. пределом посл-ти.

Экспонента или число е. Ф-ции одной переменной. Обратные ф-ции. 6. Экспонента или число е

Р-рим числ. посл-ть с общим членом xn=(1+1/n)^n (в степени n)(1) . Оказывается, что посл-ть (1) монотонно возр-ет, ограничена сверху и сл-но явл-ся сходящейся, предел этой пос-ти наз-ся экспонентой и обозначается символом е» 2,7128…

Док-ть сходимость посл-ти (1)

Для док-ва введем вспом-ю ф-цию y=(1+x)^1/x, x>0 Ясно что при знач. x=1,1/2,1/3,…,1/n,… значение ф-ции y совпадает с соответствующими эл-ми (1).

Док-м что ф-ция у монотонно убывает и огран. сверху => монотонное возр. посл-ти (1) и ограниченность ее сверх. Поскольку lg x явл-ся монотонно возр., но монотонное убыв. ф-ции у и ее огранич. сверху эквивалентны том, что ф-ция lgy, которая равняется 1/хlg(1+x) (2) имеет те же самые св-ва, т.е. 0<x1<x2, то тогда 1/x1* lg(1+x1)>1/x2* * lg(1+x2) (3). Огранич. сверху $ M:1/xlg(1+x)£ lgM " x>0 (4). Возьмем любую лин. ф-цию вида y=kx которая превосходит lg(1+x) при всех x>0.

tga 1=(lg(1+x1))/x1 a 1>a 2=>tga 1>tga 2

tga 2=(lg(1+x2))/x2

Поскольку a 1>a 2, то tga 1>tga 2, а это равносильно равенству (3). Поскольку y>lg(1+x) " x>0 => kx>

>lg(1+x) " x>0

Принимая во внимания ф-ции у с пос-ть xn приходим к нужному утверждению. Число е явл-ся неизбежным спутником динамических процессов: почти всегда показатели изменяющиеся во времени характеризующие такие процессы зависят от времени через экспонициальную ф-цию y=e^x и ее модификации.

Пр-р: если ставка сл-ных % равна r и инвестор положил в банк первоначальный вклад равный Р причем % начисляются m раз в год (r- годовая ставка) тогда через n- лет наращенная сумма нач-ся по ф-ле сл. % при m кратном их начислению.

Sn=P(1+r/m)^mn (5) Предположим теперь % нач-ся непрерывным образом, т.е. число периодов нач-ния неограничено ув-ся. Мат-ки это соотв-ет тому, что выражение (5) надо р-равать, как общий член посл-ти Xm, а непрерывному нач-нию соот-ет наращенная ф-ция lim(n® ¥ )P(1+r/m)^mn=Pe^rn

Lg(e)x имеет спец. Обозначение lnx.

Принцип вложенных отрезков

Пусть на числовой прямой задана посл-ть отрезков [a1,b1],[a2,b2],…,[an,bn],…

Причем эти отрезки удовл-ют сл. усл.:

1) каждый посл-щий вложен в предыдущий, т.е. [an+1,bn+1]Ì [an,bn], " n=1,2,…;

2) Длины отрезков ® 0 с ростом n, т.е. lim(n® ¥ )(bn-an)=0. Посл-ть с указанными св-вами наз-ют вложенными.

Теорема Любая посл-ть вложенных отрезков содержит единную т-ку с принадлежащую всем отрезкам посл-ти одновременно, с общая точка всех отрезков к которой они стягиваются.

Док-во {an}-посл-ть левых концов отрезков явл. монотонно не убывающей и ограниченной сверху числом b1.

{bn}-посл-ть правых концов монотонно не возрастающей, поэтому эти посл-ти явл. сходящимися, т.е. сущ-ют числа с1=lim(n® ¥ )an и с2=lim(n® ¥ )bn => c1=c2 => c - их общее значение. Действительно имеет предел lim(n® ¥ )(bn-an)= lim(n® ¥ )(bn)- lim(n® ¥ )(an) в силу условия 2) o= lim(n® ¥ )(bn-an)=с2-с1=> с1=с2=с

Ясно что т. с общая для всех отрезков, поскольку " n an£ c£ bn. Теперь докажем что она одна.

Допустим что $ другая с‘ к которой стягиваются все отрезки. Если взять любые не пересекающиеся отрезки с и с‘, то с одной стороны весь “хвост” посл-тей {an},{bn} должен нах-ся в окрестностях т-ки с‘‘(т.к. an и bn сходятся к с и с‘ одновременно). Противоречие док-ет т-му.

Принцип вложенных отрезков

Т-ма. Любая пос-ть вложенных отрезков содержит единств. т-ку сÎ всем отрезкам посл-ти одновременно, к которой они стягиваются.

Док-во. {an} пос-ть левых концов явл. монотонно неубыв. И огран. свеху числом b1; посл-ть правых концов {bn} монотонно не возр. и ограничена снизу а1, поэтому эти посл-ти сходящ., т.е. $ числа c1=lim(n® ¥ )an и c2=lim(n® ¥ )bn.

Докажем что с1=с2 и сл-но их общая знач. может обозначить через с. Действ. имеется предел lim(n® ¥ )(bn-an)= lim(n® ¥ )bn® lim(n® ¥ )an=c2-c1=c ясно что с общая для всех отрезков поскольку для " n an£ c£ bn. Осталось доказать единство данной т-ки (от противного). Допустим есть c‘¹ c к которой стягиваются все отрезки. Если взять любые пределы окр. точек с и с‘, то с одной стороны весь “хвост” {an}, {bn}, должен нах-ся в окрестности т-ки с, а др. в с‘, т.к. an и bn® c и c‘ одновр. Противореч. док-ет т-му.

7.Ф-ции одной переменной

Если задано правило по которому каждому значению перем. Величины х из мн-ва Х ставится соответствие 1 значению перем. У то в этом случае говорят, что задана ф-ция 1-й переменной.

Y=f(x); x –аргумент независ. перемен., y- зав. пер.

X=Df=D(f) y={y;y=f(x),xÎ X} x1Î X1, y1=f(x1)

1) аналит. способ; 2)Табличный способ;

3) Графический способ;

4)Min и max ф-ции: ф-ция f(x) ограничена, если огран. ее мн-во знач У, т.е. $ m,M: m£ f(x)£ M " xÎ X

m£ f(x) " xÎ X => огр. сн.; f(x)£ M, " xÎ X=> огр. св.

Обратные ф-ции

Если задано правило по которому каждому значению yÎ Y ставится в соответствие ® ед. знач. х, причем y=f(x), то в этом случае говорят, что на мн-ве Y определена ф-ция обратная ф-ции f(x) и обозначают такую ф-цию x=f^-1(y).

Предел ф-ции в точке. Свойства предела ф-ции в точке. Односторонние пределы ф-ции в т-ке:. Предел ф-ции в т-ке. Предел и непрерывность функции. Предел. Односторонний предел. Предел ф-ции в точке

y=f(x) X

опр. " {xn} Ì X, xn® x0

f(xn)® A,=> f(x) в т. x0 (при , xn® x0) предел = А

А=lim(x® x0)f(x) или f(x)® A при x® x0

Т-ка x0 может Î и Ï мн-ву Х.

Свойства предела ф-ции в точке

1) Если предел в т-ке сущ-ет, то он единственный

2) Если в тке х0 предел ф-ции f(x) lim(x® x0)f(x)=A

lim(x® x0)g(x)£ B=> то тогда в этой т-ке $ предел суммы, разности, произведения и частного. Отделение этих 2-х ф-ций.

а) lim(x® x0)(f(x)± g(x))=A± B

б) lim(x® x0)(f(x)* g(x))=A* B

в) lim(x® x0)(f(x):g(x))=A/B

г) lim(x® x0)C=C

д) lim(x® x0)C* f(x)=C* A

Док-во xn® x0, $ lim(x® x0)f(x)=A по опр. f(xn)® A {f(xn)}

Односторонние пределы ф-ции в т-ке:

Опр. А - предел ф-ции f(x) справа от точки х0, если f(x)® A при х® х0, и x>x0

Формально это означает, что для любой посл-ти {xn}® x0, вып-ся условие xn>x0, f(x)® A. Обозначим f(x0+0) и f(x0+) lim(x® x0+0)f(x)®

И также с минусами.

Признак $ предела

Т-ма Для того чтобы f(x) имела предел в т-ке х0 необх., тогда в этой т-ке ф-ция f имеет совпадающ. Между собой одностор. предел (f(x0+)=f(x0-) (1), которые равны пределу ф-ции.

Док-во. f(x) имеет в т-ке х0 предел А, тогда f(x)® A независимо от того приближается ли х к х0 по значению больше х0 или меньше это означает равенство (1)

Предел ф-ции в т-ке

Число А наз-ся пределом ф-ции в т-ке х0 если " e >0 найдется такое число В>0, для всех х отличных от х0 и (х-х0)<0 должно ½ f(x)-A½ <e

" e >0 из ½ х-х0½ <d должно быть

Пусть ½ f(x)-x0½ <e , если d =e , то ½ х-х0½ <d => ½ f(x)-x0½ <e

Свойства пределов. Непрерывность ф-ции.

Ф-ция f(x) непрерывна в т-ке х0 если предельное значение в этой т-ке равно самому знач. в этой точке.

Предел и непрерывность функции

Пусть ф-ция f(x) определена на некотором пр-ке Х* и пусть точка х0Î Х или х0Ï Х.

Опр. Число А наз-ся пределом ф-ции f(x) в точке х=х0, если для " e >0 $ d >0 такое, что для всех хÎ Х, х¹ х0, удовлетвор. неравенству ½ х-х0½ <e , выполняется неравенство ½ f(x)-A½ <e .

Пример Используя определение, док-ть что ф-ция f(x)=C(C-некоторое число) в точке х=х0(х0-любое число) имеет предел, равный С, т.е. lim (x® x0)C=C

Возьмем любое e >0. Тогда для любого числа d >0 выполняется треюуемое неравенство ½ f(x)-C½ =½ C-C½ =0<e , => lim(x® x0)C=C

Свойства пределов. Непрерывность ф-ции.

Теорема. Пусть ф-ции f(x) и g(x) имеют в т-ке х0 пределы В и С. Тогда ф-ции f(x)± g(x),f(x)g(x) и f(x)/g(x) (при С¹ 0) имеют в т-ке х0 пределы, равные соответственно В± С, В* С, В/С, т.е. lim[f(x)± g(x)]= B± C, lim[f(x)* g(x)]= B* C, lim[f(x)/g(x)]= B/C

Теорема также верна если х0 явл. + ¥ , - ¥ , ¥

Опр. Ф-ция f(x) наз-ся непрерыной в точке х=х0, если предел ф-ции и ее значение в этой точке равны, т.е. lim(x® x0)f(x)=f(x0)

Теорема Пусть ф-ции f(x) и g(x) непрерывны в т-ке х0. Тогда ф-ции f(x)± g(x), f(x)* g(x) и f(x)/g(x) также непрерывны в этой т-ке.

10. Предел. Односторонний предел.

Опр.Числом А наз-ся предел f(x) в т-ке х0, если для любой окрестности А$ окрестность (х0):" xÎ окрестности (x0) выполняется условие f(x)Î окрестности.

Теорема Все определения предела эквивалентны между собой.

Опр. Число А называется пределом ф-ции f(x) справа от т.х0(правым предело f(x0)) если f(x)® A при х® х0, х>x0

Формально это означает, что для любой посл-ти сходящейся к х0 при xn>x0 выполняется условие f(xn)® A

Запись: f(x0+o), f(x0+ ). lim(x® x0+o)f(x) где запись x® x0+o как раз означает стремление к х0 по мн-ву значений >чем х0.

Опр. Предел слева аналогично и исп-ся запись f(x0-o);f(x0-)

Теорема. Для того чтобы ф-ция f(x) имела предел в точке х0 необходимо и достаточно когда в этой т-ке ф-ция имеет совпадающие между собой одностороние пределы (f(x0+)=f(x0-)) значение которые равны пределу ф-ции, т.е. f(x0+)=

f(x0-)=lim(x® x0)f(x)=A

Док-во

а) допустим ф-ция имеет в точке х0 предел равный А, тогда f(x)® А независимо от того, приближается ли х к х0 по значению > x0 или <, а это означает равенство 1.

б) пусть односторонние пределы сущ-ют и равны f(x0+)=f(x0-) докажем, что $ просто предел. Возьмем произвольную {xn}® х0 разобьем если это необходимо эту последовательность на две подпоследовательности.