Выполнил: ученик 11 Б класса Назаркин Павел Дмитриевич
Муниципальное общеобразовательное учреждение «Лицей №43»
Саранск, 2004
Постановка задачи.
Произвести необходимые расчеты для нахождения минимальной скорости тела, брошенного через прямоугольное препятствие.
Методы выполнения работы.
Для выполнения данной работы проделаем ряд математических вычислений и преобразований с использованием физических формул.
Зная, что траекторией движения тела, является парабола, а также математическую формулу записи данной линии, будем использовать уравнение параболы общего вида в качестве начальных данных поставленной задачи. В выбранной нами прямоугольной системе координат запишем данное уравнение для двух точек, принадлежащих линии движения – начальной точке А и точке В, в которой тело окажется через некоторый промежуток времени t. Решая систему полученных при этом уравнений, путем математических замен и преобразований выведем формулу зависимости движения тела от одной переменной L, т.е. коэффициенты k и b, участвующие в общем виде уравнения параболы, выразим через L. Затем, используя физический закон движения тела, брошенного под углом к горизонту, выразим переменную L через ![]() и V . В результате получим уравнение движения, в качестве коэффициентов в котором будут выступать переменные
и V . В результате получим уравнение движения, в качестве коэффициентов в котором будут выступать переменные ![]() и V. Затем составим систему двух уравнений, полученных подстановкой координат точек А и В в последнее уравнение движения. Решая данную систему, мы найдем неизвестные нам величины
и V. Затем составим систему двух уравнений, полученных подстановкой координат точек А и В в последнее уравнение движения. Решая данную систему, мы найдем неизвестные нам величины ![]() и V, выразив их через имеющиеся известные нам параметры – ширину и высоту прямоугольного препятствия. Для нахождения Vmin воспользуемся производной функции.
и V, выразив их через имеющиеся известные нам параметры – ширину и высоту прямоугольного препятствия. Для нахождения Vmin воспользуемся производной функции.
Решение.
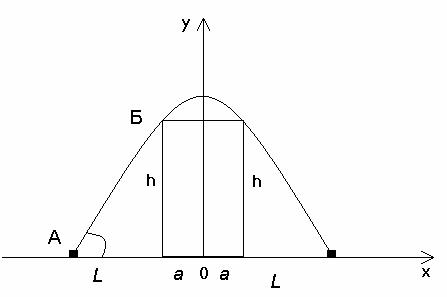
Уравнением линии движения тела, брошенного через прямоугольное препятствие, в общем виде является уравнение параболы :
y=-kx2+b
Введем прямоугольную систему координат и свяжем ее с прямоугольным препятствием, как показано на рисунке.
В данной системе координат уравнение движения тела в точках А и Б примет вид:
![]() 0=-k(a+L)2+b,
0=-k(a+L)2+b,
h=-ka2+b.
Выразим k и b через одну неизвестную L:
Вычитаем 1)-ое из 2)-ого:
h=k(a2+2aL+L2-a2),
h=k(2aL+L2) ,![]() (*);
(*);
![]()
![]() h=b-ka2+b b=h+ka2
h=b-ka2+b b=h+ka2 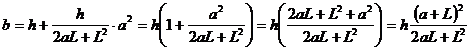 . (*)
. (*)
Получилось, что уравнение движения зависит только от L:
y=-kx2+b, где коэффициенты k и b имеют вид (*).
Найдем зависимость L от![]() и V.
и V.
Из курса физики известно: что движение тела, брошенного под углом горизонта описывается уравнениями
![]()
![]()
![]() x=Vxt L=Vxt L=Vcos
x=Vxt L=Vxt L=Vcos![]() t
t
![]()
![]() y=Vyt+gt2/2 h=Vyt-gy t2/2 gt2-2Vyt+2h=0.
y=Vyt+gt2/2 h=Vyt-gy t2/2 gt2-2Vyt+2h=0.
gt2-2Vyt+2h=0.
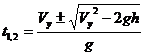 .
.
Мы рассматриваем время движения от точки А до Б, значит
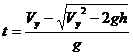 , где Vy=Vsin
, где Vy=Vsin![]() .
.
Итак, 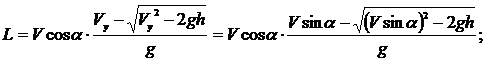
Умножив обе части уравнения на g, получим:
![]() (1)
(1)
Известно, что 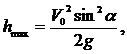 т.е.
т.е. ![]()
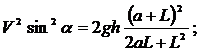 (2)
(2)
С другой стороны tg![]() =y’ в точке А, т.е. tg
=y’ в точке А, т.е. tg![]() =y’(-a-L);
=y’(-a-L);
![]()
Подставив значение tg![]() в (2), получим:
в (2), получим:
V2sin2![]() =g(a+L) tg
=g(a+L) tg ![]()
![]()
![]() V2sin
V2sin![]() cos
cos![]() =g(a+L) Lg=V2sin
=g(a+L) Lg=V2sin![]() cos
cos![]() -ga (3)
-ga (3)
Сравнив (1) и (3) получаем, что:
![]()
![]() .
.
Получили уравнение с двумя неизвестными V и![]() : выразив V через
: выразив V через ![]() , мы получим ту самую функцию, которую мы должны были найти:
, мы получим ту самую функцию, которую мы должны были найти:
Пусть z=V2, тогда z cos2![]() (z sin2
(z sin2![]() -2gh)=g2a2;
-2gh)=g2a2;
z2 cos2![]() sin2
sin2![]() - z cos2
- z cos2![]() 2gh-g2a2=0;
2gh-g2a2=0;
Получили квадратное уравнение относительно z
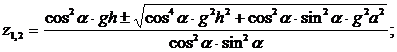
Очевидно, ![]() значит, т.к. z=V2>0, то
значит, т.к. z=V2>0, то 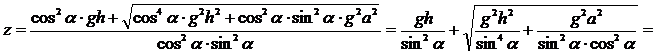
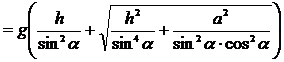 .
.
Вместо зависимости V от ![]() рассмотрим зависимость z от
рассмотрим зависимость z от ![]() , и обозначив
, и обозначив ![]() получим зависимость z от t.
получим зависимость z от t.
Получим ![]() , где z=V2,
, где z=V2, ![]() .
.
Выразим ![]() через t, если
через t, если ![]() ;
; ![]()
![]()
Значит, ![]()
Т.е. 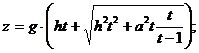
![]()
Таким образом, чтобы найти Vmin и ![]() , нам нужно во-первых, найти fmin и t.
, нам нужно во-первых, найти fmin и t.
![]()
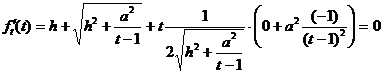 .
.
Умножив обе части уравнения на ![]() , получим
, получим
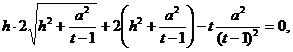
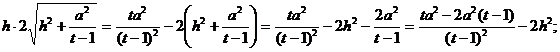
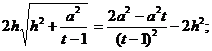
Прежде чем возвести обе части в квадрат, сделаем предварительный анализ получившегося уравнения: т.к. ![]()
то и ![]()
т.е. ![]() и
и ![]()
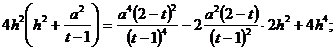
![]()
![]()
![]()
Умножив обе части уравнения на (t-1)2, получим
![]()
![]()
![]() Т.к t<2 и t>1 (т.к.
Т.к t<2 и t>1 (т.к. ![]() ), то можно извлечь корень.
), то можно извлечь корень.
![]()
![]()
![]()
![]()
![]()
![]()
![]() ; (4)
; (4)
![]()
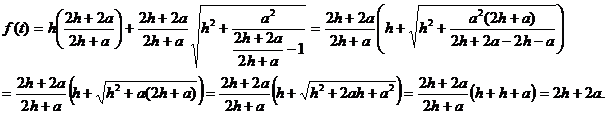
 Итак, f(t)=2h+2a, значит
Итак, f(t)=2h+2a, значит ![]() .
.
Т.к. z=V2, то ![]() т.е.
т.е. ![]() (5)
(5)
Осталось найти L:
Его найдем используя (3).
![]()
![]()

![]()
![]()

![]()
![]()
Результаты работы.
Проделанным расчетом мы нашли зависимость скорости, движения брошенного через прямоугольное препятствие тела, так чтобы она была минимальной, от длины и высоты прямоугольного препятствия. То есть, зная данные препятствия, - его длину и ширину – а так же формулы, полученные в данной работе, мы можем определить на каком расстоянии от препятствия, под каким углом и с какой минимальной скоростью необходимо бросить тело, чтобы оно перелетело через это препятствие.
Актуальность темы.
Данные расчеты и выведенные формулы используются в различных сферах деятельности человека. В частности, в военной практике, для правильного расчета движения траектории снарядов.
Приложение.
К работе прилагается программа, результатом которой является вывод на экран траектории движения тела, брошенного через прямоугольное препятствие. Входными параметрами программы являются данные прямоугольного препятствия – его длина и высота. Программа написана на языке программирования Delphi.
Для подготовки данной работы были использованы материалы с сайта http://licey43.ru
Похожие работы
... биологических и химических средств защиты леса от хвое- и листогрызущих насекомых». Наставление разработано на основе обобщения результатов исследований по совершенствованию технологий изменения средств защиты леса от вредителей на базе современной авиационной техники. Данный документ рассматривает такие важные для лесозащитной практики вопросы, как определение целесообразности авиационной борьбы ...
... инерциальных системах отсчета. Пространственно-временной континуум – неразрывная связь пространства и времени и их зависимость от системы отсчета. Тема 11. Основные концепции химии 1. Химия как наука, ее предмет и проблемы Важнейшим разделом современного естествознания является химия. Она играет большую роль в решении наиболее актуальных и перспективных проблем современного общества. К ...
... , да вайте сделаем красивое панно "Цветы на лугу". Мы его по весим в вестибюле и будем любоваться этими цветами, как будто у нас в детском саду еще лето, веселое, солнечное. Хорошо? Ответы детей 2. Работа по теме Разъясняет особенности коллективной деятельности: "Теперь каждый из вас пусть подумает, какие он хочет вырезать цветы. Затем вы будете приклеивать свои цветы на большой лист ...
... -судебных задач обусловила необходимость разработки ряда специальных криминалистических рекомендаций с учётом отдельных положений таких наук, как химия, физика, математика. Как отрасль криминалистической техники судебная баллистика представляет собой систему научно-технических средств и методов обнаружения, фиксации, изъятия и исследования объектов с целью определения их видовой (групповой) ...
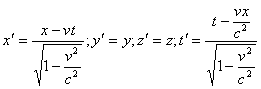


0 комментариев