Навигация
Вычисление площади поверхности
5. Вычисление площади поверхности.
Пусть требуется вычислить площадь поверхности, ограниченной линией Г (рис.20); поверхность задана уравнением ![]() где функция
где функция ![]() непрерывна и имеет непрерывные частные производные. Обозначим проекцию линии Г на плоскость Oxy через L. Область на плоскости Oxy, ограниченную линией L, обозначим D.
непрерывна и имеет непрерывные частные производные. Обозначим проекцию линии Г на плоскость Oxy через L. Область на плоскости Oxy, ограниченную линией L, обозначим D.
Разобьём произвольным образом область D на n элементарных площадок ![]() В каждой площадке
В каждой площадке ![]() возьмём точку
возьмём точку ![]() Точке Pi будет соответствовать на поверхности точка
Точке Pi будет соответствовать на поверхности точка ![]() Через точку Mi проведём касательную плоскость к поверхности. Уравнение её примет вид
Через точку Mi проведём касательную плоскость к поверхности. Уравнение её примет вид
![]() (1)
(1)
На этой плоскости выделим такую площадку ![]() , которая проектируется на плоскость Оху в виде площадки
, которая проектируется на плоскость Оху в виде площадки ![]() . Рассмотрим сумму всех площадок
. Рассмотрим сумму всех площадок ![]()
Предел ![]() этой суммы, когда наибольший из диаметров площадок
этой суммы, когда наибольший из диаметров площадок ![]() - стремится к нулю, мы будем называть площадью поверхности, т. е. по определению положим
- стремится к нулю, мы будем называть площадью поверхности, т. е. по определению положим
![]() (2)
(2)
Займемся теперь вычислением площади поверхности. Обозначим через ![]() угол между касательной плоскостью и плоскостью Оху.
угол между касательной плоскостью и плоскостью Оху.
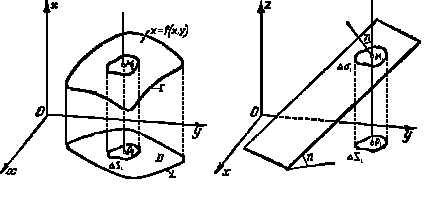
Рис.20 Рис.21
На основании известной формулы аналитической геометрии можно написать (рис.21)
![]()
или
![]() (3)
(3)
Угол ![]() есть в то же время угол между осью Oz и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеем
есть в то же время угол между осью Oz и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеем
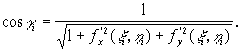 Следовательно,
Следовательно,
![]()
Подставляя это выражение в формулу (2), получим
![]()
Так как предел интегральной суммы, стоящей в правой части последнего равенства, по определению представляет собой двойной интеграл 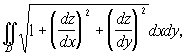 то окончательно получаем
то окончательно получаем
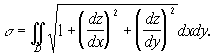 (4)
(4)
Это и есть формула, по которой вычисляется площадь поверхности ![]()
Если уравнение поверхности дано в виде ![]() или в виде
или в виде ![]() то соответствующие формулы для вычисления поверхности имеют вид
то соответствующие формулы для вычисления поверхности имеют вид
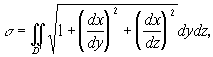 (3’)
(3’)
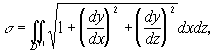 (3’’)
(3’’)
где D’ и D’’ - области на плоскостях Oyz и Oxz, в которые проектируется данная поверхность.
а) Примеры.
Пример 1. Вычислить поверхность ![]() сферы
сферы
![]()
Решение. Вычислим поверхность верхней половины сферы ![]() (рис.22). В этом случае
(рис.22). В этом случае
![]()
Следовательно, подынтегральная функция примет вид
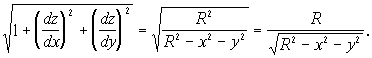
Область интегрирования определяется условием ![]() . Таким образом, на основании формулы (4) будем иметь
. Таким образом, на основании формулы (4) будем иметь
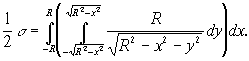
Для вычисления полученного двойного интеграла перейдём к полярным координатам. В полярных координатах граница области интегрирования определяется уравнением ![]() Следовательно,
Следовательно,
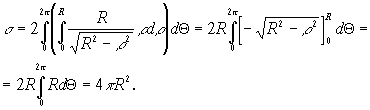
Пример2. Найти площадь той части поверхности цилиндра ![]() которая вырезается цилиндром
которая вырезается цилиндром ![]()
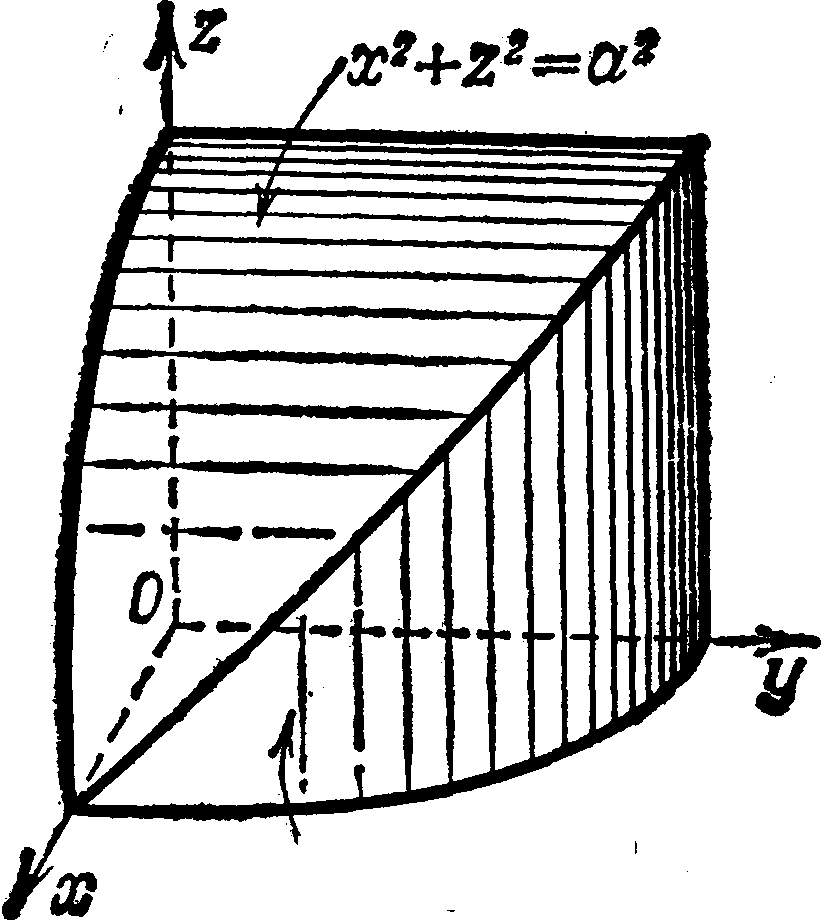
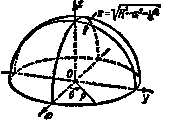
Рис.22 Рис.23
Решение. На рис.23 изображена ![]() часть искомой поверхности. Уравнение поверхности имеет вид
часть искомой поверхности. Уравнение поверхности имеет вид ![]() ; поэтому
; поэтому
![]()
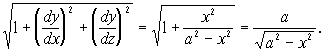
Область интегрирования представляет собой четверть круга, т.е. определяется условиями ![]()
Следовательно, 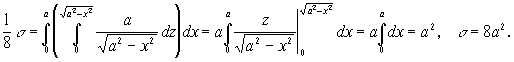
Список использованной литературы.
А.Ф. Бермант ,И.Г. Араманович
Краткий курс математического анализа для втузов: Учебное пособие для втузов: - М.: Наука, Главная редакция физико-математической литературы , 1971 г.,736с.
Н.С. ПискуновДифференциальное и интегральное исчисления для втузов, Том 2:
Учебное пособие для втузов.-13-е изд. -М. :Наука, Главная редакция физико-математической литературы, 1985.-560с.
В.С. ШипачёвВысшая математика: Учебное пособие для втузов: - М: Наука,
Главная редакция физико-математической литературы.
Похожие работы
... формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано. Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa). Само слово ...
... выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала. В “Мемуаре об исчислении вариаций кратных ...
... Спорщики возьмут в руки перья и, сказав: “Начнем вычислять” - примутся за расчеты. Как уже отмечалось, Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование - взаимно обратные операции. Об этом свойстве хороню знал и ...
... все содержание посылок, поскольку оно необходимо для вывода, имеет нечувственный характер. (аксиомы, постулаты). VI. Интуитивизм, индивидуалистический эмпиризм и априоризм критической философии в их отношении к теории элементарных методов знания. Три ответа на вопрос о происхождении общих суждений: 1) Путем прямых методов (прямой индукции) = интуитивизм. 2) Общих суждений нет Только иллюзия. ( ...
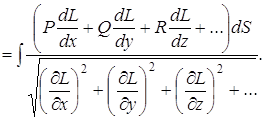
0 комментариев