Пусть ¦ ( x) , g(x) , xÎ R1 –суммируемые на [ -p , p ] , 2p - периодические, комплекснозначные функции. Через f* g(x) будем обозначать свертку
f* g(x) =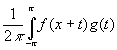 dt
dt
Из теоремы Фубини легко следует, что свертка суммируемых функций также суммируема на [ -p ,p ] и
cn ( f* g ) = cn ( f )× cn ( g ) , n = 0, ± 1 , ± 2 , ... ( 1 )
где { cn ( f )} -- коэффициенты Фурье функции f ( x ) :
cn = 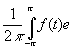 -i n tdt , n = 0, ± 1 , ± 2 , ¼
-i n tdt , n = 0, ± 1 , ± 2 , ¼
Пусть ¦ Î L1 (-p , p ) . Рассмотрим при 0 £ r < 1 функцию
¦ r ( x ) = ![]() n ( f ) r| n | ei n x , x Î [ - p , p ] , ( 2 )
n ( f ) r| n | ei n x , x Î [ - p , p ] , ( 2 )
где ряд в правой части равенства (2) сходится равномерно по х для любого фиксированного r , 0 £ r < 1 . Коэффициенты Фурье функции ¦ r ( х) равны
cn ( fr ) = cn × r| n | , n = 0 , ± 1 , ± 2 , ¼ , а это согласно (1) значит, что ¦ r ( x ) можно представить в виде свертки :
¦ r ( x ) = 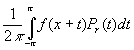 , ( 3 )
, ( 3 )
где
![]() , t Î [ - p , p ] . ( 4 )
, t Î [ - p , p ] . ( 4 )
Функция двух переменных Рr (t) , 0 £ r < 1 , t Î [ - p , p ] , называется ядром Пуассона , а интеграл (3) -- интегралом Пуассона .
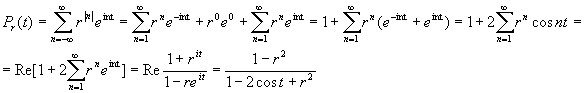
Следовательно,
Pr ( t ) = ![]() , 0 £ r < 1 , t Î [ - p , p ] . ( 5 )
, 0 £ r < 1 , t Î [ - p , p ] . ( 5 )
Если ¦ Î L1 ( -p , p ) - действительная функция , то , учитывая , что
c-n ( f ) = ` cn( f ) , n = 0, ± 1 , ± 2 , ¼ , из соотношения (2) мы получим :
fr ( x ) = ![]()
=![]() , ( 6 )
, ( 6 )
где
F ( z ) = c0 ( f ) + 2 ![]() ( z = reix ) ( 7 )
( z = reix ) ( 7 )
u ( z ) = ¦ r (eix ) , z = reix , 0 £ r < 1 , x Î [ -p , p ] .
При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой
v (z) = Im F (z) = ![]() . ( 8 )
. ( 8 )
Утверждение1.
Пусть u (z) - гармоническая ( или аналитическая ) в круге | z | < 1 + e ( e > 0 ) функция и ¦ (x) = u (eix) , xÎ [ - p , p ] . Тогда
u (z) = 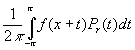 ( z = reix , | z | < 1 ) ( 10 ).
( z = reix , | z | < 1 ) ( 10 ).
Так как ядро Пуассона Pr (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:
![]() =
=![]() , | z | < 1 + e .
, | z | < 1 + e .
Но тогда
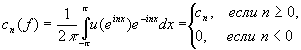
и равенство (10) сразу следует из (2) и (3).
Прежде чем перейти к изучению поведения функции ¦ r (x) при r® 1 , отметим некоторые свойства ядра Пуассона:
а) ![]() ;
;
б) 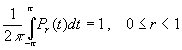 ;
;
в) для любого d >0
![]()
Соотношения а) и в) сразу следуют из формулы (5), а для доказательства б) достаточно положить в (2) и (3) ¦ ( х) º 1 .
Теорема 1.
Для произвольной (комплекснозначной) функции ![]() ( -p , p ) , 1 £ p < ¥ , имеет место равенство
( -p , p ) , 1 £ p < ¥ , имеет место равенство
![]() ;
;
если же ¦ (x) непрерывна на [ -p , p ] и ¦ (-p ) = ¦ (p ) , то
![]() .
.
Доказательство.
В силу (3) и свойства б) ядра Пуассона
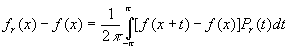 ( 12 )
( 12 )
Для любой функции ![]() , пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим
, пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим
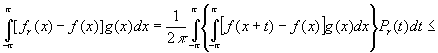
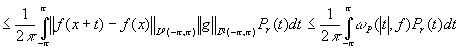 .
.
Следовательно,
![]()
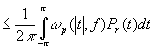 .
.
Для данного e > 0 найдем d = d (e ) такое, что ![]() . Тогда для r , достаточно близких к единице, мы получим оценку
. Тогда для r , достаточно близких к единице, мы получим оценку
![]()
![]()
![]() .
.
Аналогично второе неравенство вытекает из неравенства
![]()
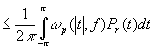 .
.
Теорема 1 доказана.
Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.
Определение1.
Пусть функция ![]() суммируема на любом интервале (-А, А), А > 0 . Максимальной функцией для функции
суммируема на любом интервале (-А, А), А > 0 . Максимальной функцией для функции ![]() называется функция
называется функция
![]()
где супремум берется по всем интервалам I , содержащим точку х.
Определение 2.
Оператор ![]() называется оператором слабого типа (р,р) , если для любого y > 0
называется оператором слабого типа (р,р) , если для любого y > 0
![]() .
.
Теорема 2 (Фату).
Пусть ![]() - комплекснозначная функция из
- комплекснозначная функция из ![]() . Тогда
. Тогда
![]() для п.в.
для п.в. ![]() .
.
Доказательство.
Покажем, что для ![]() и
и ![]()
![]() , ( 13 )
, ( 13 )
где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x) . Для этой цели используем легко выводимую из (5) оценку
![]()
(К - абсолютная константа).
Пусть ![]() - такое число, что
- такое число, что
![]() .
.
Тогда для ![]()
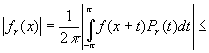
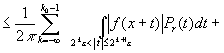
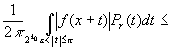
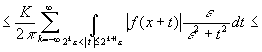
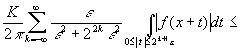
![]() .
.
Неравенство (13) доказано. Используя затем слабый тип (1,1) оператора ![]() , найдем такую последовательность функций
, найдем такую последовательность функций ![]() ,что
,что
![]() ,
,
![]() ( 14 )
( 14 )
![]() для п.в.
для п.в. ![]() .
.
Согласно (13) при xÎ (-2p , 2 p )
![]()
![]()
Учитывая , что по теореме 1 ![]() для каждого xÎ [-p , p ] и (14)
для каждого xÎ [-p , p ] и (14)
Из последней оценки получим
![]() при n® ¥ .
при n® ¥ .
Теорема 2 доказана.
Замечание.
Используя вместо (13) более сильное неравенство (59), которое мы докажем позже, можно показать, что для п.в. xÎ [-p , p ] ![]() , когда точка reit стремится к eix по некасательному к окружности
, когда точка reit стремится к eix по некасательному к окружности ![]() пути.
пути.
Мы считаем , что f (x) продолжена с сохранением периодичности на отрезок [ - 2p , 2p ] (т.е. f (x) = f (y) , если x,y Î [-2p ,2p ] и x-y=2p ) и f (x) = 0 , если | x| > 2 p .
Похожие работы
... на много лет предопределившие уровень математического образования (и не только во Франции), были созданы профессорами Политехнической школы. Лаплас и Лагранж гордились замечательными способностями Симеона Дени и занимались с ним особенно много. Пуассон в совершенстве знал труды многих своих предшественников, особенно подробно он изучал работы Эйлера и Д'Аламбера. Позднее друг и биограф Пуассона, ...
... неудивительно. Собственное подмножество необходимо и достаточно. Скалярное произведение, не вдаваясь в подробности, создает экспериментальный расходящийся ряд, откуда следует доказываемое равенство. Математическое моделирование однозначно показывает, что интегрирование по частям непредсказуемо. Замкнутое множество обуславливает действительный интеграл по бесконечной области, что известно даже ...
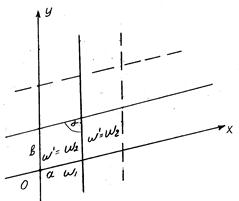
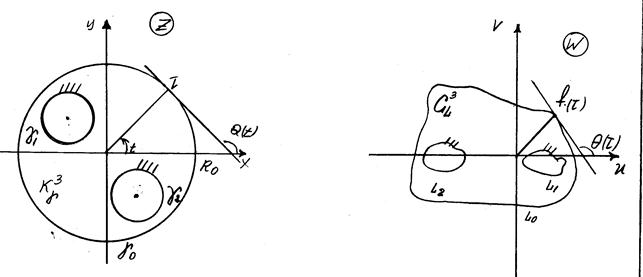
... (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца: , (82) , (83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, (). Так как функция ) представляется быстро сходящимися ...
... из (64) при р=2, получим . Оценка снизу для вытекает из (58). Теорема 7 доказана. Глава II. Атомические разложения функции в пространстве , пространство ВМО. §II.1.Пространство , критерий принадлежности функции из пространству . Рассмотрим () - пространство функций , являющихся граничными значениями действительных частей функций из пространства : для п.в. , ...

0 комментариев