tg(α+β)=(tgα+tgβ)/(1–tgα·tgβ); tg(α-β)=(tgα–tgβ)/(1+tgα·tgβ)
ctg(α+β)=(ctgα·ctgβ–1)/(ctgβ+ctgα); ctg(α+β)=(ctgα·ctgβ+1)/(ctgβ–ctgα)
sinα+sinβ=2sin½(α+β)cos½(α-β); sinα-sinβ=2cos½(α+β)sin ½(α-β)
cosα+cosβ=2cos½(α+β)cos½(α-β); cosα-cosβ=-2sin½(α+β)sin ½(α-β)
a·sinx+b·cosx=Ö (a²+b²)sin(x+β), где tgβ=b/a
tgα ± tgβ=sin(α+β)/(cosα·cosβ); ctgα ± ctgβ=sin(β± α)/(sinα·sinβ)
sin²α–sin²β=cos²β–cos²α=sin(α+β)sin(α-β)
cos²α–sin²β=cos²β–sin²α=cos(α+β)cos(α-β)
sinα·sinβ=½[cos(α-β)–cos(α+β)]; cosα·cosβ=½[cos(α-β)+cos(α+β)]
sinα·cosβ=½[sin(α+β)+sin(α-β)]
tgα·tgβ=(tgα+tgβ)/(ctgα+ctgβ)=-(tgα–tgβ)/(ctgα–ctgβ)
ctgα·tgβ=(ctgα+tgβ)/(tgα+ctgβ)=-(ctgα–tgβ)/(tgα–ctgβ)
ctgα·ctgβ=(ctgα+ctgβ)/(tgα+tgβ)=-(ctgα–ctgβ)/(tgα–tgβ)
sin½α=± Ö ((1–cosα)/2); sinα=(2tg½α)/(1+tg² ½α)
sin2α=2 sinα·cosα; sin3α=3sinα–4sin³α
sin²α=½(1–cos2α); sin³α=(3 sinα – sin 3α) / 4
cos½α=± Ö [(1+cosα)/2]; cosα=(1–tg² ½α)/(1+tg² ½α)
cos2α=cos²α–sin²α=1–2 sin²α=2cos²α–1; cos3α=4cos³α–3 cosα
cos²α=½(1+cos2α);cos³α=(3cosα+cos3α)/4
tg½α=sinα/(1+cosα)=(1–cosα)/sinα= ± Ö ((1–cosα)/(1+cosα))
tgα=(2tg½α)/(1–tg² ½α); tg2α=(2tgα)/(1–tg²α)=2/(ctgα–tgα)
tg3α=(3tgα–tg³α)/(1–3tg²α)=tgα·tg(π/3+α)·tg(π/3–α)
ctg½α=sinα/(1–cosα)=(1+cosα)/sinα=± Ö ((1+cosα)/(1–cosα))
ctgα=(ctg² ½α–1)/2ctg ½α; ctg2α=(ctg²α–1)/2ctgα=½(ctgα–tgα)
ctg3α=(3ctgα–ctg³α)/(1–3 ctg²α)
tg(¼п+α)=(sinα+cosα)/(sinα–cosα); tg(¼п–α)=(sinα–cosα)/(sinα+cosα)
Похожие работы
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
дробно рассмотрено преобразование групп общих решений тригонометрических уравнений. В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе. В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и ...
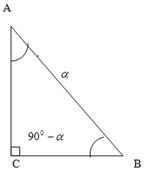
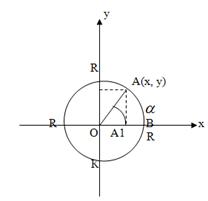
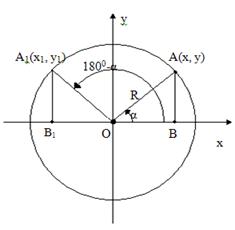
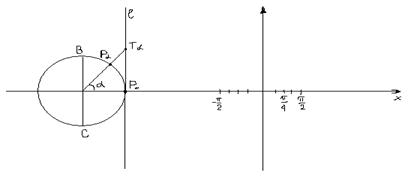
... угол 1800-α= по гипотенузе и острому углу: => OB1=OB; A1B1=AB => x = -x1,y = y1=> Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности. Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного ...
... при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции. С понятием функции связаны два способа решения уравнений: графический и функциональный. Частным случаем функционального метода является метод функциональной, или универсальной подстановки. Определение. Решить данное уравнение – значит найти множество всех его корней (решений). Множество ...






0 комментариев