Навигация
Логика доказательств и физическое происхождение условий некоторых математических теорем
2. Логика доказательств и физическое происхождение условий некоторых математических теорем
Выведем из физических соображений некоторые ограничения на функцию, которая может служить законом движения макроскопического тела, а затем сравним их с условиями основных теорем дифференциального исчисления.
(А) Начнем с простого соображения о том, что реальный физический эксперимент имеет свое начало и конец, т.е. протекает за конечный отрезок времени. В силу этого можно считать, что закон движения тела представляет собой функцию, определенную на отрезке [a, b].
(Б) Рассмотрим более глубокий вопрос о том, всякая ли числовая функция числового аргумента может служить законом движения для некоторого физического тела. Наивный, но любопытный студент может задать такой вопрос в отношении многих хорошо известных ему функций: s(t) = t2, s(t) = t, s(t) = sint, s(t) = tgt, s(t) = sgnt и т.д. При этом в некоторых случаях ответ хорошо известен (равноускоренное и колебательное движение в первом и третьем случае соответственно), а в других отнюдь не очевиден.
На самом деле ответ на поставленный вопрос является отрицательным, поскольку закон движения макроскопического тела является непрерывной функцией. Докажем это на е − δ-языке с помощью эйнштейновского постулата о постоянстве скорости света c. Пусть функция s(t) выражает закон движения тела. Если она разрывна в точке u, то справедливо следующее утверждение:
(Зе > 0)(V5 > 0)(3t, | t − u |< δ) | s(0 - s(u) |≥ ε. (3)
Рассмотрим числа ε и t, фигурирующие в утверждении (3). Подберем число δ достаточно малым для того, чтобы дробь ε оказалась больше скорости света в вакууме:
ε>c. (4)
8 V '
Вычислим теперь модуль средней скорости на промежутке от u до t. Пользуясь двумя неравенствами в соотношении (3) и неравенством (4), получаем, что
. | s(0 - s(u) | ε ε
|t−u | |t−u | δ
а это противоречит положению о недостижимости скорости света физическим телом. Если обращение к эйнштейновскому постулату по каким-либо причинам нежелательно, непрерывность закона движения тела можно пояснить с помощью наглядных соображений, касающихся разрывов того или иного типа. Например, закон движения тела не может иметь "бесконечный" разрыв, поскольку в этом случае материальное тело пройдет бесконечное расстояние за конечное время. Аналогичные рассуждения можно провести в отношении разрывов типа "скачок" и типа "колебание".
Сравним в физическом контексте две функции: функцию s: [0,1) →> R, заданную равенством s(t) =1, и функцию s : [0,1 ] →> R, заданную равенством s(t) =1. Очевидно, что функция s является сужением функции s на некоторое подмножество области определения, или, другими словами, функция s является продолжением функции s на более широкое множество. Хорошо известно, что под действием операции продолжения (сужения) функция может терять некоторые из своих свойств или приобретать новые свойства. В данном случае различие в свойствах имеет физическую природу: функция s может служить законом движения некоторого тела, а функция s не может, поскольку в противном случае тело удалилось бы на бесконечность за конечное время. Функции s и s можно рассматривать в контексте теории рядов, поскольку выражение является суммой бесконечно убывающей геометрической прогрессии
1 +t +t2 +t3 + L. Известно, что областью сходимости этого степенного ряда является интервал (−1,1). Таким образом, для данного примера получаем, что сходимость степенного ряда тесно связана со способностью его суммы служить законом движения тела. (В) Покажем, что среди функций, описывающих движения макроскопического тела, всегда можно выбрать дифференцируемую функцию.
Начнем с примера. Пусть легкий упругий шарик падает на массивную плиту и отскакивает от нее. Для изучения движения шарика построим две модели. Первая модель базируется на следующих допущениях: 1) шарик представляет собой материальную точку; 2) отскок происходит мгновенно. Вторая модель базируется на двух других допущениях: 1) шарик представляет собой тело конечного объема, а закон движения описывает положение центра тяжести шарика; 2) отскок происходит за конечное время за счет деформации шарика. Нетрудно видеть, что первая модель представляет собой функцию, не дифференцируемую в те моменты времени, которые соответствуют моментам отскока. В то же время вторая модель является функцией, дифференцируемой при любых значениях аргумента.
Мы оставляем в стороне вопросы об адекватности данных моделей физическому явлению, об удобстве использования каждой из них, о целесообразности выбора той или иной модели при исследовании движения шарика в разные моменты времени. Здесь мы хотим лишь подчеркнуть, что каждая пара допущений является вполне естественной. Поясним возможность выбора дифференцируемой модели в точных терминах. Известно, что для каждой функции s(t), непрерывной на отрезке [a, b], можно построить интерполяционный многочлен Лагранжа Ln(t) с помощью n узлов интерполирования. Более того, можно выбрать такую последовательность систем узлов, что выражение
I s(t) − Ln(t) | будет равномерно сходиться к нулю при и n → ∞ [3. C. 265]. Это означает, что какова бы ни была точность измерения с помощью физических приборов, существует номер N, такой, что при всех n> N величина | s(t) − Ln(t) | меньше точности измерения. Отсюда следует, что многочлен Лагранжа Ln(t), который является дифференцируемой функцией, можно принять за закон движения тела, причем расчеты с помощью многочлена Ln (t) и измерения при данной точности будут соответствовать друг другу.
К сожалению, приведенное рассуждение не может быть предъявлено в тот момент, когда происходит изучение основных теорем дифференциального исчисления, поскольку теория интерполяции изучается значительно позднее.
Обратимся теперь к основным теоремам дифференциального исчисления. Теорема Лагранжа [3. C. 226] и многочисленные следствия из нее справедливы для функций, которые удовлетворяют ряду условий: функции определены на замкнутом отрезке, непрерывны на нем и дифференцируемы внутри него. Очевидно, что эти условия полностью совпадают с теми свойствами законов движения тел, которые выведены в пунктах (А)-(В) из чисто физических соображений. Тем самым выявляется двойственная природа условий теорем дифференциального исчисления. С одной стороны, введение этих условий вызвано потребностями логики, поскольку каждое из них используется при доказательстве теорем, а невыполнение любого из них приводит к тому, что теоремы перестают быть справедливыми. С другой стороны, мы обнаружили, что эти чисто логические ограничения на функции оказались детерминированы свойствами окружающего нас физического мира.
В рамках данной статьи будем пользоваться следующим определением. Назовем функцию f(x) подобной закону движения тела, если она определена на отрезке [a, b], непрерывна на нем и дифференцируема на интервале (a,b).
Не всякая функция, подобная закону движения тела, может служить законом движения реального физического тела. Двумя простыми примерами являются функции
f(x) = arcsin(x) и f(x) = x , определенные на отрезке [0,1]. Обе они подобны закону движения тела, однако не могут служить законами движения для реального физического тела, поскольку достигают бесконечных скоростей, первая в момент окончания
движения, а вторая даже в момент его начала. Таким образом, между множеством функций, являющихся законами движения, и множеством функций, подобных закону движения, существует отношение включения: первое множество включается во второе. 3. Специальная методика изложения основных теорем дифференциального исчисления
Идея предлагаемой методики проста и естественна. Она состоит в том, чтобы побудить студентов к обоснованному переносу свойств функций из класса законов движения тела на более широкое множество - класс функций, подобных закону движения тела.
1) Как показал эксперимент, большинство студентов понимают, что для закона движения тела существует момент времени t0, для которого справедлива формула (2). Если распространить это утверждение на более широкое множество, то мы можем сформулировать следующую гипотезу. Гипотеза 1 (Лагранж). Если функция f(x) подобна закону движения тела, то существу-
г„ ч f(b)−f(a) ет такое значение аргумента x0 , что / (jc0) = ^-^) .
Нетрудно увидеть в этой гипотезе теорему Лагранжа. Нетрудно также заметить, что преподаватель может использовать дополнительное рассуждение для пояснения естественности рассматриваемой гипотезы. Действительно, в процессе движения скорость варьируется между своим минимальным и максимальным значением. Естественно предположить, что в какой-то момент времени ее значение совпадет со средней скоростью тела.
2) Как показал эксперимент, большинство студентов понимают, что если движущееся тело занимает одно и тоже положение в начальный и конечный моменты времени, то в момент t0 наибольшего удаления s′(t0) = 0. Если распространить это утверждение на более широкое множество, то мы можем сформулировать следующую гипотезу. Гипотеза 2 (Ролль). Если функция f(x) подобна закону движения тела на отрезке [a,b] и f(a) = f(b), то существует такое значение аргумента x0 , что f′(x0) = 0.
Нетрудно увидеть в этой гипотезе теорему Ролля. Нетрудно также заметить, что преподаватель может использовать дополнительное рассуждение для пояснения естественности рассматриваемой гипотезы. Действительно, допустим, что в момент наибольшего
удаления скорость тела больше нуля. Тогда тело, двигаясь по инерции, удалится от начала движения на расстояние, превосходящее расстояние максимального удаления. Очевидно, что последнее невозможно по чисто логическим соображениям. Аналогично отвергается случай отрицательной скорости в момент наибольшего удаления.
3) Выведем критерий постоянства функции из физических соображений. Тот факт, что тело покоится в течение некоторого промежутка времени, можно выразить в одной из двух равносильных форм. Во-первых, можно сказать, что координата тела является константой, а во-вторых, что скорость тела тождественно равна нулю:
s(t) ≡ const <=> Тело покоится <=> s'(0 = 0.
Удалив из рассуждения промежуточные звенья, мы получим, что для любого закона движения тела справедливо утверждение s(0 = const <=> s′(t = 0.
Если распространить полученную эквиваленцию на более широкий класс функций, а именно, на множество функций, подобных закону движения тела, то мы придем к следующей гипотезе.
Гипотеза 3 (Постоянство функции). Функция, подобная закону движения тела, постоянна тогда и только тогда, когда ее производная тождественно равна нулю: f(x) ≡ const <=> f′(x) ≡ 0.
4) Если скорость тела положительна, то это означает, что оно движется вперед без остановок, и следовательно, его координата возрастает. Другими словами, получаем, что для любого закона движения тела справедливо утверждение
s′(t) = v(t) > 0 => s(t) возрастает.
Если распространить полученную импликацию на более широкий класс функций, а именно, на множество функций, подобных закону движения тела, то мы придем к следующей гипотезе.
Гипотеза 4 (Достаточное условие монотонности). Если функция подобна закону движения тела и ее производная положительна, то функция возрастает: f′(x) > 0 => f(x) возрастает.
Подобные рассуждения можно было бы провести в отношении других теорем дифференциального исчисления. Многократные проверки показали, что студенты легко справляются с задачей распространения свойств движений на более широкий класс функций и самостоятельно получают в виде гипотез все основные теоремы дифференциального исчисления.
В заключение отметим, что возникновение математических утверждений в виде гипотез отнюдь не заменяет их строгого логического доказательства, даже если в процессе самостоятельного вывода этих утверждений студенты продемонстрировали способность к математическому творчеству. В то же время нельзя недооценивать этот творческий акт. Даже с утилитарной точки зрения он дает преподавателю большую свободу в отношении дальнейших математико-педагогических действий. Проверку гипотез можно сделать немедленной или отсроченной, выполнить эту проверку самому или отослать студентов к учебникам, заняться применением этих гипотез в физике или математике и проч. Выбор педагогом того или иного способа действий зависит от конкретной ситуации.
Список литературыКолмогоров А.Н. Математика в ее историческом развитии. - М.: Наука, 1991. - 223 с. Нейман, Дж. фон. Математик // Природа. - 1983. - № 2. - С. 88-95. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 1. - М.: Наука, 1966.-607 с.
Ястребов А.В. Использование интуиции студентов в преподавании дифференциального исчисления // Актуальные методические и психолого-педагогические проблемы обучения в высшей школе. Тезисы докладов II областной научно методической конференции. -Ярославль: Изд-во Ярославского гос. университета, 1990. - С. 35-36. Ястребов А.В. Моделирование научных исследований как средство оптимизации обучения студента педагогического вуза // Дисс.…. д-ра пед. наук. - Ярославль, 1997. - 38
Похожие работы
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
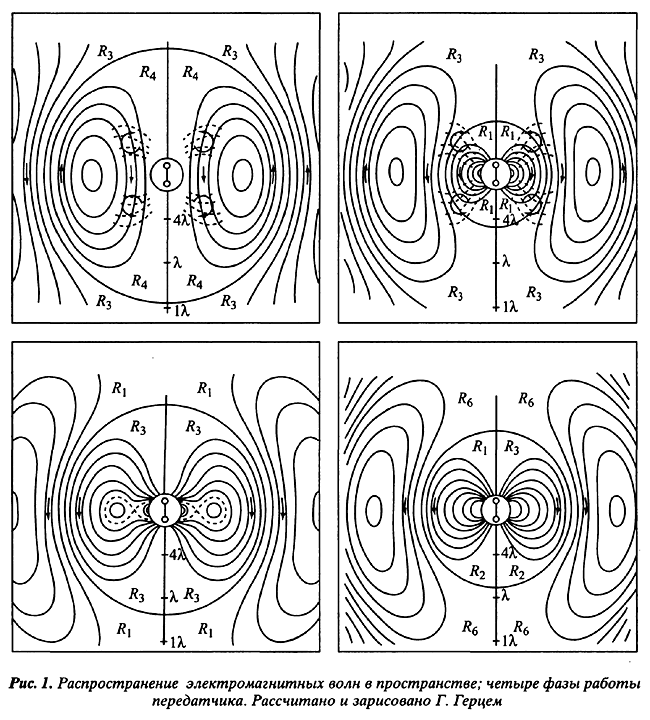
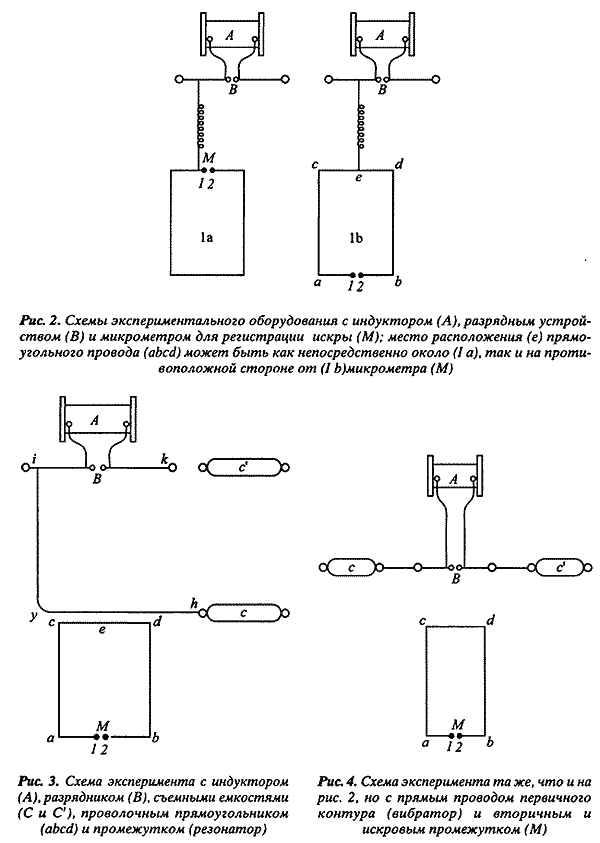
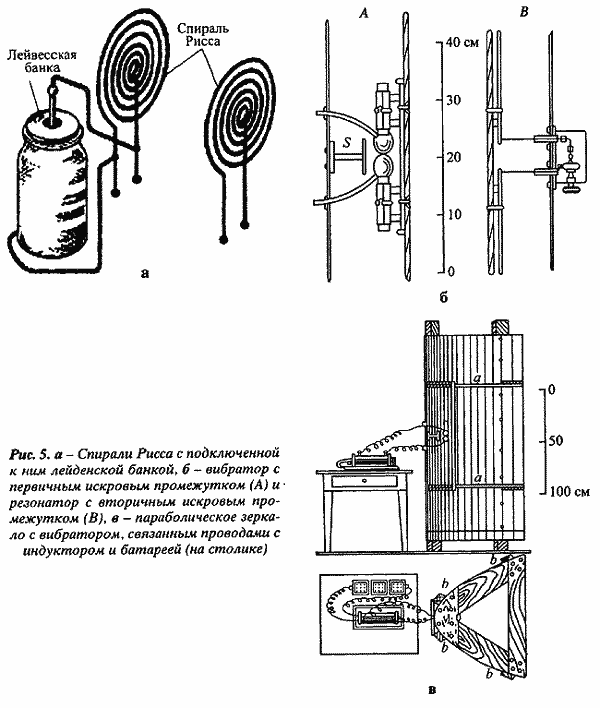
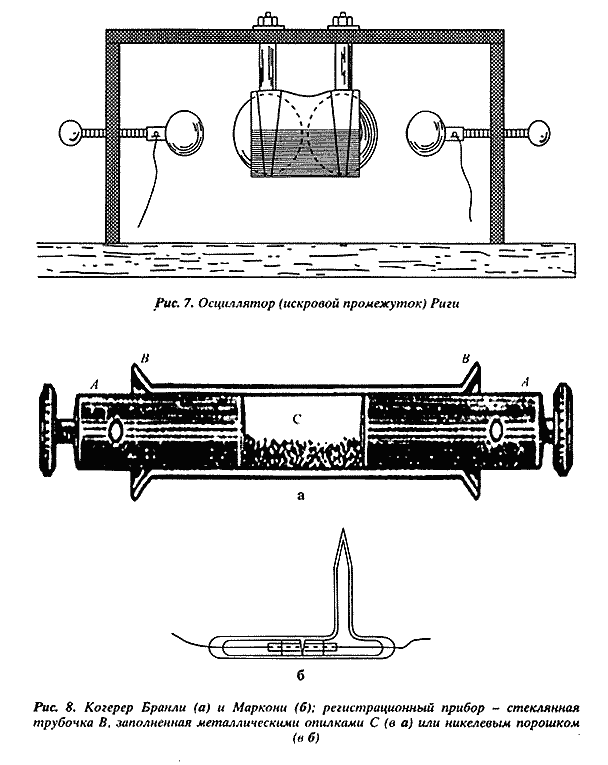
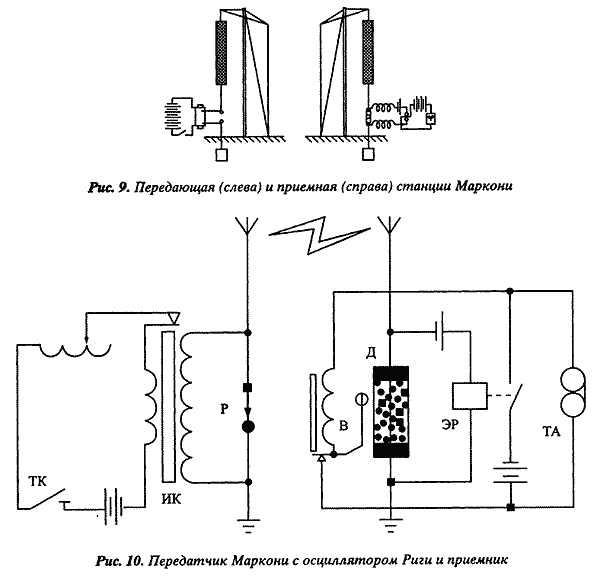
... анализа генезиса теоретических схем технических наук в процессе модификации теоретических схем соответствующей базовой физической теории (электродинамики). Экспериментальное доказательство Герцем теории Максвелла и его технические следствия Заимствованная из механики и акустики теоретическая схема естественного волнового процесса позволяла транслировать для случая электромагнитных волн и ...
... формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано. Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa). Само слово ...
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
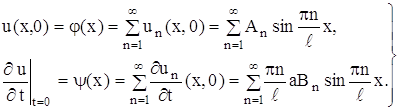
0 комментариев