Реферат
Эквивалентность пяти классов функций элементарных по Кальмару
студента группы ТК
четвертого курса
Польщи М.В.
Научный руководитель: профессор Лисовик Леонид Петрович
Определение. Функция называется элементарной по Кальмару, если ее можно получить й из функций s1, Inm, x+y, x-y, S, а также конечного применения операций суммирования и мультиплицирования.
Определим пять классов функций, элементарных по Кальмару.
L1 Класс функций, получаемый из функций s1, Inm, x+y, x-y, S, а также конечного применения операций суммирования и мультиплицирования.
L2 Класс функций, получаемый из функций s1, Inm, x-y, 2x ,S, а также конечного применения операции суммирования.
L3 Класс функций, получаемый из функций s1, Inm, x-y, x*y, 2x ,S, а также конечного применения операции ограниченной минимизации.
L4 Класс функций, получаемый из функций s1, Inm, x-y, x+y 2x ,S, а также конечного применения операции ограниченной рекурсии.
L5 Класс функций, получаемый из функций s1, Inm, x-y, x*y, S, а также конечного применения операции мультиплицирования.
Доказательство будем проводить по следующей схеме:
1. L1L2L3L4L1
2. L1L5
3. L5L3
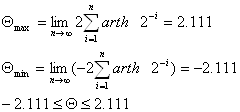
Докажем, что L1L2 (для этого выразим 2x через функции L1 )
![]()
Докажем, что L2L3 (для этого выразим x*y и операцию ограниченной минимизации через функции L2 )
![]()
Пусть
![]() тогда
тогда
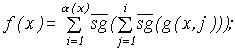
![]()
Докажем, что L3L4 (для этого выразим x+y и операцию ограниченной рекурсии через функции L3 )
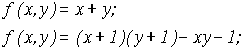
Выразим операцию ограниченной рекурсии на основании следующего свойства функции Геделя.
![]()
Пусть
![]() тогда
тогда
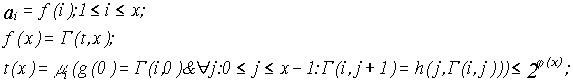
Отношение, примененное в операция конечной минимизации, является элементарным по Кальмару.
Докажем, что L4L1 (для этого выразим операции суммирования и мультиплицирования через функции L4)
Выразим м3ультиплицирование через ограниченную рекурсию.
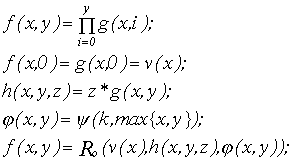
Где (x,y)-к-ступенчатая функция.
Выразим суммирование через ограниченную рекурсию.
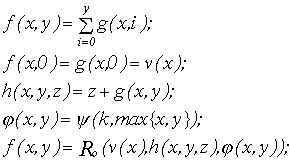
Докажем, что L1L5 (для этого выразим x*y через функции L5 )
![]()
Докажем, что L5L3 (для этого выразим 2x и операцию ограниченной минимизации выразим через функции L5 )
![]()
Пусть
![]() тогда
тогда
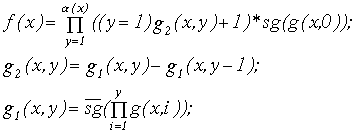
Эквивалентность классов доказана.
Похожие работы
ть специализированный математический процессор для вычисления элементарных функций arcSin(Z) и arCth(Z). Эти функции можно реализовать методом Волдера «Цифра за цифрой», метод Меджита и др. Оба эти метода основаны на ряде итерационных формул, которые приведены в таблице 1.1. Основное их различие заключается в том, что в методе Меджита на первом этапе сразу рассчитываются все направляющие ...
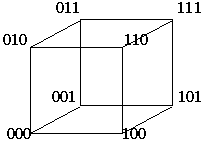
... значения, получим геометрическое представление функции. Например, булева функция, заданная табл.1, геометрически представляется 3-мерным кубом (рис. 1.в). а) n=1 б) n=2 в) n=3 Рисунок 1- Геометрическое задание булевой функции: а) одной переменной: б) двух переменных; в) трех переменных. При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, ...
... , в смысле совпадения отражающих функций, дифференциальной системы, стационарной или нестационарной, качественный портрет решений которой известен. В данной работе рассматривается задача о построении дифференциальных систем, эквивалентных в смысле совпадения отражающих функций, системам с известным первым интегралом. §1. Отображение Пуанкаре Рассмотрим систему Будем считать, что ...
и эквивалентно заданию двух действительных функций и тогда , где , . Как и в обычном анализе, в теории функций комплексной переменной очень важную роль играют элементарные функции. Рассмотрим некоторые из них. 1. - линейная функция. Определена при всех . Отображает полную комплексную плоскость на полную комплексную плоскость . Функция и обратная ей - однозначны. Функция поворачивает плоскость ...
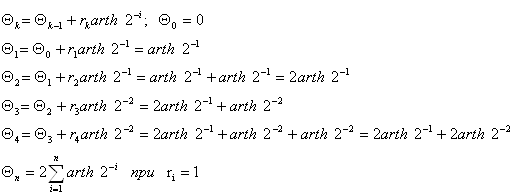



0 комментариев