основные тригонометрические тождества;
доказательство формул;
мнемоническое правило.
Свойства тригонометрических функций:
sin x, y= cos x, y= tg x, y= ctg x.
Их графики.
Определения синуса, косинуса, тангенса и котангенса через тригонометрический круг.
Простейшие тригонометрические уравнения.
Определения и свойства обратных тригонометрических функций: y= arcsin x, y= arccos x, y= arctg x, y= arcctg x.
Их графики.
Простейшие тригонометрические неравенства (sin x < a).
Любая производная из листа, таблицы.
Правила вычисления производной (Лагранж).
Геометрический смысл производной:
производная в данной точке;
уравнение касательной;
угол между прямыми.
Физический смысл производной.
Экстремумы функций. Правила нахождения их с помощью производной.
Возрастание и убывание функции. Правило Лагранжа.
Наибольшее и наименьшее значение функции. Правила. На эту тему.
Многочлены. Теорема Безу, ее доказательство.
Правила нахождения рациональных корней, доказательство.
Четность, периодичность.
Вычислить cos 22,5° sin(arcsin11/12)-cos(arccos1/6) tg(arcsin21/29) tg(arccos1/4) tg(arcctg7) sin(arccos1/3)-cos(arcsin(-1/3)) sin(arctg12)+cos(arcctg(-2)) cos(arctg(-5))-sin(arctg3) cos(p /2+arcsin3/4) cos(p -arctg17) cos(3p /2+arcctg(-4)) cos(2p -2arccos(-Ö 3/2)) sin(p /2-arccos1/10) sin(p +arctgÖ 3/7) sin(3p /2-arcctg81) sin(2p -3arcsinÖ 2/2) tg(p /2-arccos(-1/3)) tg(3p /2+4arctgÖ 3/3) tg(p +arcsin(-2/17)) tg(2p -arcctg(-5)) arcsin(-Ö 3/2) arcsin1 arcsin(-1) arccos(-Ö 3/2) arccos0 arccos(-1) arctg(-1/Ö 3) arctg(-1) arctg1 arcctg(-1/Ö 3) arcctg(-1) arcctg0 cos(arctg2) sin(arctg(-3/4)) tg(arcctg(-3)) sin(arcctg p) tg(arcsin p), -1<p<1 ctg(arctg p), p¹ 0 arcsin(-Ö 3/2)+arcctg(-1)+arccos(1/Ö 2)+1/2arccos(-1) sin(1/2arcctg(-3/4)) ctg(1/2arccos(-4/7)) tg(5arctgÖ 3/3-1/4arcsinÖ 3/2) sin(3arctgÖ 3+2arccos1/2) os(3arcsinÖ 3/2+arccos(-1/2)) sin(1/2arcsin(-2Ö 2/3)) Какой знак имеет число: cosÖ 3 sin2× sin4× sin6 cos5× cos7× cos8 tg(-1)× tg3× tg6× tg(-3) ctg1× ctg(-2)× ctg9× ctg(-12) sin(-3)× cos4× tg(-5) / ctg6 sin7× cos(-8) / tg6× ctg(-5) (sin6+cos(-4)) / (tg(-2)+ctg(-10)) (sin(-8)+cos9) / cos11tg(-9) (cos10× sin7-tg10) / cos(-Ö 2)× ctg(-4) arcsin(tg(-1/2))+arctg(cos(-4)) sin(-212° ) sin3p /7× cos9p /8× tg2,3p sin1× cos3× ctg5 sin1,3p × cos7p /9× tg2,9 sin8× cos0,7× tg6,4 sin7p /6× cos3p /4 sin5p /3× cos2p /5× cos7p /4 sin1,3× cos(-1,5)× sin(-1,9) sin23° -sin36° cos37° -cos18° cosp /9-cos2p /9 cos212° -cos213° sin310° -sin347° cos5p /6-cos5p /7 sinp /12-sinp /18 cos3p /7-cos3p /11 cosp /11-sinp /11 sin2p /3-cos3p /4 sin16° -cos375° ctg153° -ctg154° tg319° -tg327° tg(33p /8)-tg(37p /9) ctg(101p /14)-ctg(251p /27) tgp /6-ctgp /4 tgp /6-ctgp /6 Решить уравнения: sin(x2 + x) =1/2; 4 - сos2 x = 4sinx 5 - 2cosx = 5Ö 2sin(x/2) cos4x = cos2x sin4x + cos4x = sin2x-1/2 sin2x + 3sin2x - 2сos2x = 2 cos(x/2) + 3/2sinx + 5sin2(x/2) = 3 sinx - 2cosx = 1 cos6x + sin6x - cos22x = 1/16 cos2x - sin3x× cosx + 1 = sin2x + sinx× cos3x tgx - tg2x = sinx 2sin3x - cos2x - sinx = 0 2cos2x = Ö 6(cosx - sinx) 1 - sinx = cosx - sin2x 2Ö 3sin2(x/2) + 2 = 2sin2x + Ö 3 1 + cos(x2 + 1) = sin2(x2 + 1) 2sinx× cos2x + cos4x = 2sinx + cos2x + cos2x tg2x + ctg2x + 3tgx + 3ctgx +4 = 0 1 + cos(x/2) + cosx = 0 1 - sin(x/2) = cosx 2sin2x + cos4x = 0 sin4x + 2cos2x = 1 5sinx - 4ctgx = 0 3cosx + 2tgx = 0 1 + 4cosx = cos2x 2cos2x + 5sinx + 1 = 0 cos2x + 3Ö 2sinx - 3 = 0 2cos2x + 4cosx =sin2x 2cos2x + sin3x = 2 cos4x + 4sin2x = 1 + 2sin22x 4 - 6cosx = 3 sin2x - sin2(x/2) 5 + 2sin2x - 5cosx = 5sinx cos4x + 8sin2x - 2 = 6cos2x - 8 cos4x 4 - 3cos4x = 10sinx× cosx sin4x = (1 +Ö 2)(sin2x + cos2x - 1) cos(10x + 12) + 4Ö 2sin(5x + 6) = 4 sin3x + cos3x = 1 - 1/2sin2x ctg2x - tg2x = 16cos2x 1 + sinx + cosx + sin2x + cos2x = 0 1/2(cos2x + cos22x) - 1 = 2sin2x - 2sinx - sinx - sin2x tg(p /2× cosx) = ctg(p /2× sinx) sin3x - sinx + cos2x = 1 2cos2x + 3sinx = 0 2sin2x + 1/cos2x = 3 2sin2x + Ö 3cosx = 0 Ö 1 + sinx¢ + cosx = 0 sin4x + cos4x = sin2x 4cos4x + 6sin22x + 5cos2x = 0 cos2x + 4sin3x = 1 1 - sin2x = -(sinx + cosx) 4sin22x - 2cos22x = cos8x 8sin4x + 13cos2x = 7 2sinx + 3sin2x = 0 cos(x/2) = 1 + cosx sin2x = 1 + Ö 2cosx + cos2x sin2x = Ö 3sinx 2cos23x - cos3x = 0 Ö 3sin2x = 2cos2x 3sin2x - cos2x - 1 = 0 Ö 3sin2x - cos2x = Ö 3 Доказать:tg208° <sin492°
Что больше:sin1 или cos1
tg1 или tg2
Похожие работы
деление 1.2. Пара , где – непустое множество, а (возможно, пустое) множество операций на , называется универсальной алгеброй или, короче, алгеброй. Совокупность операций (или опрерационных символов) будем называть сигнатурой. Часто, при введении алгебры, указывают только множество и не указывают сигнатуру. Элемент алгебры отмечаемый -арной операцией . будем обозначать через . Определение ...
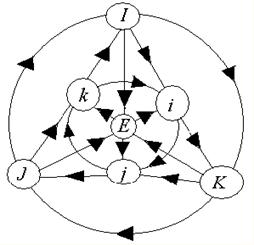
... следовательно, система аксиом алгебры октав категорична ввиду изоморфности произвольных ее моделей. §2. Дополнительные сведения об октавах В ходе доказательства непротиворечивости системы аксиом алгебры октав мы установили, что любую октаву можно представить в виде: w = a+bi+cj+dk+ Ae+BI+CJ+DK, где a,b,c,d, a,b,c,d R и i2 = j2 = k2 = e2=I2= j2 = k2 = -1, причем iе = I, je = J, ke = ...
... ,1973.-339с. 10. Higgins P.J. Groups with multiple operators //Proc. London math.Soc.-1956.-V.6,--№3.-p. 366--416. Отзыв на дипломную работу ``Свойства централизаторов конгруэнций универсальных алгебр'' студентки 5 курса математического факультета Шутовой И.Н. Дипломная работа Шутовой И.Н. посвящена решению задачи изучения формационных свойств подалгебр универсальных алгебр.В отличии от ...
... понятия собственного числа линейного оператора А. 120. Определите, каким является базис а=(1/, 1/,1/), b=(1/, -1/, 0), с =(1/, 1/,-2/). Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЛИНЕЙНАЯ АЛГЕБРА Билет № 26 121. Приведение матрицы к ступенчатому виду методом Гаусса. Пример. 122. ...
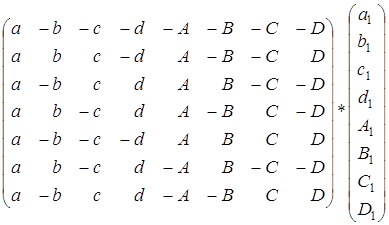
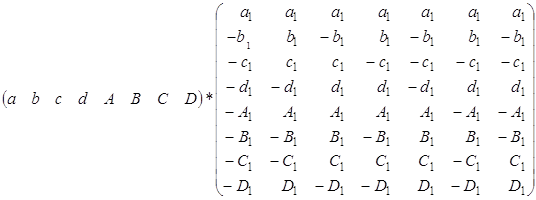
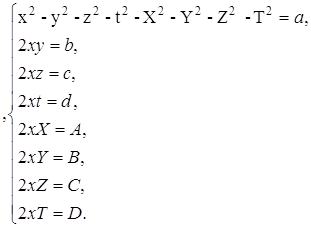
0 комментариев