/***************************************************************************** * .FILE : numeric.c * .TITLE : (парабол) * .DESCR : Курсовой проект по численным методам (1994 год) * : * : Выполнил: Петренко В.С. (гр. ПС-301) * : Проверил: Панюков А.В. * : * .NOTE : NOT FOR RENTAL OR SALE. * : FEDERAL LAW PROVIDES SEVERE CIVIL & CRIMINAL PENALTIES FOR * : UNAUTHORIZED DUPLICATION OR DISTRIBUTION. * : * : (C) '94 by P$P *****************************************************************************/ #include <math.h> #include <stdio.h> /***************************************************************************** * .NAME : m_Simpson * .TITLE : Расчет интеграла методом Симпсона (парабол) * .DESCR : * : * .PARAMS : double m_Simpson (double (*func) (double, double), * : double t_fix, double t_limit, int N); * : double (*func) (double, double) - подынтегральная ф-я * : double t_fix - фиксированный первый аргумент * : double t_limit - верхний предел интегрирования, * : нижний равен -t_limit * : int N - число точек разбиения * .RETURN : Значение вычисленного интеграла *****************************************************************************/ double m_Simpson (double (*func) (double, double), double t_fix, double t_limit, int N) { double sum1 = 0; /* -¬ */ double sum2 = 0; /* ¦ временные переменные */ double sum3 = 0; /* -- */ double sum; /* конечный результат */ double h = (2 * t_limit) / N; /* шаг сетки */ int i; /* временная */ sum1 = (*func) (t_fix, -t_limit) + (*func) (t_fix, +t_limit); for (i = 1; i <= N - 1; i++) sum2 += (*func) (t_fix, -t_limit + (i * h)); sum2 *= 2; for (i = 1; i <= N; i++) sum3 += (*func) (t_fix, -t_limit + ((i-0.5) * h)); sum3 *= 4; sum = sum1 + sum2 + sum3; sum = (h / 6) * sum; return sum; } /* */ /* Глобальные переменные */ /* ~~~~~~~~~~~~~~~~~~~~~ */ #define PI 3.1415926536 /* число П */ double k; /* параметр функции - задается пользователем */ int N_MAX; /* число узлов сетки разбиения */ double (*currFunc) (double, double); /* выбранная пользователем функция */ double f1 (double x, double y); double f2 (double x, double y); double f3 (double x, double y); /***************************************************************************** * .NAME : double F (double dummy, double t) * .TITLE : Вычисляет внутренний интеграл (G (t)). * : См. текст курсового проекта. * .DESCR : П/2 * : - * : первая вычисляемая функция ¦ G (t + П/2) * sin (t + П/2) dt * : t - * : - -П/2 * : где G (t) = ¦ currFunc (t, tau) dtau * : - * : -t * .PARAMS : double F (double dummy, double t); * : double dummy - фиктивный первый аргумент, при вызове этой * : функции он не используется, т.к. она * : функция одного аргумента * : double - действительный второй аргумент * .RETURN : Значение функции: G (t) * sin (k * t); *****************************************************************************/ double F (double dummy, double t) { double G; t = t + PI / 2; /* сдвижка начала координат, чтобы пределы */ /* были симметричны (в нашем случае - на П/2) */ G = m_Simpson (currFunc, t, t, N_MAX); return G * sin (k * t); } /***************************************************************************** * .NAME : main * .TITLE : Основная диалоговая функция. * .DESCR : Запрашивается интересующая пользователя функция, * : параметр k и число узлов сетки N_MAX. * : Выводит на экран вычисленное значение интеграла и * : два справочных значения - П и П/2. * : * .PARAMS : void main (void); * .RETURN : *****************************************************************************/ void main (void) { double integral; /* значение вычисленного интеграла */ int selection; /* номер выбранной функции */ /* массив доступных функций */ double (*functions []) (double, double) = { f1, f2, f3 }; printf ("n Вычисление интеграла методом Симпсона (парабол) "); printf ("n ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "); printf ("n -- "); printf ("n I = ¦¦ sin k(x + y) f (x, y) dx dy "); printf ("n -- "); printf ("n D "); printf ("n где D = { (x, y): x, y >= 0; x + y <= П }, f Е C (D)"); printf ("n"); printf ("nДля какой функции рассчитывать: "); printf ("n~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ "); printf ("n 1) f (x, y) = 0.5 * cos (y) "); printf ("n - -- 0; k != 1 "); printf ("n ¦ sin x * sin (kx) dx => ¦ "); printf ("n - L- П/2; k = 1 "); printf ("n "); printf ("n 2) f (x, y) = 0.5 - sin (y) "); printf ("n - "); printf ("n ¦ x * sin (kx) dx =====> П; k = 1 "); printf ("n - "); printf ("n "); printf ("n 3) f (x, y) = sqrt (x * x + y * y)"); printf ("n"); do { printf ("Ваш выбор: "); scanf ("%d", &selection); } while (!(1 <= selection && selection <= 3)); printf ("Параметр k: "); scanf ("%lg", &k); do { printf ("Число узлов сетки N: "); scanf ("%d", &N_MAX); } while (!(N_MAX > 0)); printf ("n"); printf ("n Расчет интеграла ..."); currFunc = functions [selection - 1]; /* текущая функция */ integral = m_Simpson (F, 0, PI / 2, N_MAX); /* вычисляем интеграл */ printf ("n Значение интеграла равно: %.12lg", integral); /* вывод */ printf ("n Величины: П = %.12lg; П/2 = %.12lg", PI, PI / 2); } /***************************************************************************** * .FILE : func.c * .TITLE : Содержит функции пользователя, которые можно * : изменять без перекомпиляции основной программы * .DESCR : После изменения этого модуля его необходимо перекомпилировать * : и слинковать с numeric.obj * : * : * .NOTE : NOT FOR RENTAL OR SALE. * : FEDERAL LAW PROVIDES SEVERE CIVIL & CRIMINAL PENALTIES FOR * : UNAUTHORIZED DUPLICATION OR DISTRIBUTION. * : * : (C) '94 by P$P *****************************************************************************/ #include <math.h> /* выбираемая пользователем функция No.1 */ double f1 (double x, double y) { return 0.5 * cos (y); } /* выбираемая пользователем функция No.2 */ double f2 (double x, double y) { return 0.5 - sin (y); } /* выбираемая пользователем функция No.3 */ double f3 (double x, double y) { return sqrt (x * x + y * y); }
Раздел:
Математика Количество знаков с пробелами: 5985
Количество таблиц: 0
Количество изображений: 0
... 580,80);
rectangle(82,12,578,78);
rectangle(85,15,575,75);
settextstyle(0,0,2);
setcolor(10);
if
ea mod 2 =0 then
begin
settextstyle(0,0,2);
outtextxy(90,20,' Вычисление
интеграл ');
outtextxy(90,50,' методом
Ньютона-Котеса.');
newsctext(ea);
end
else
begin
settextstyle(3,0,2);
outtextxy(90,20,' Calculeting of integral');
outtextxy(90,47,' ...
... “Сохранить как Web-страницу”. Вид полученного документа, отображаемого InternetExplorer 5.0 представлен на рисунке 3. Заключение В данной курсовой работе разработана программа расчета определенного интеграла по формуле Буля по схеме двойного пересчета с заданной точностью При работе над программой пройдены все этапы создания программных продуктов. Получены ...
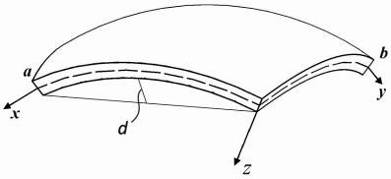
... необходимости строить локальную сети обмена данными, а достаточно сэмулировать этот процесс. Глава 4. Алгоритмы решения задач устойчивости для подкрепленных пологих оболочек, основанные на распараллеливании процесса вычисления При исследовании устойчивых подкрепленных оболочек с учетом геометрической нелинейности приходится многократно решать системы алгебраических уравнений. Коэффициенты ...
помощью метода Рунге-Кутты четвертого порядка с автоматическим выбором шага на отрезке . Задачу можно решить аналитически, найдя решение дифференциального уравнения и подставив в него начальное условие, тем самым, отыскав требуемую интегральную кривую. Но для нас интерес представляет решение данной задачи с применением численного метода, а конкретнее – метода Рунге-Кутты 4-го порядка с ...
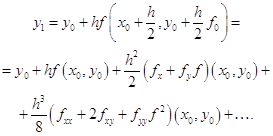
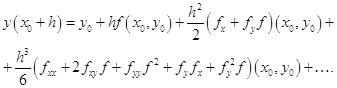
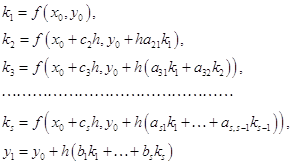
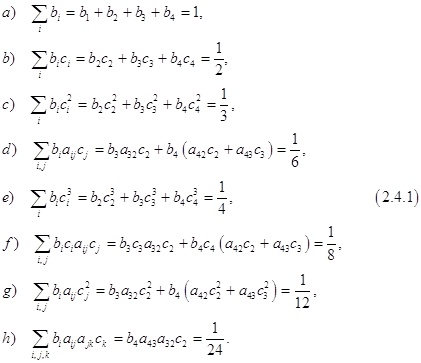
0 комментариев