Диканский Ю.И.
Один из подходов к определению эффективных полей связан с анализом действующих на дипольную частицу сил [1]. В работе [2] на основании такого анализа получена формула для расчета эффективных электрических полей в жидких диэлектриках. Механический перенос подхода, используемого при ее выводе, возможный благодаря глубокой аналогии между законами электрической поляризации и намагничивания позволяет получить аналогичную формулу для расчета эффективных магнитных полей в магнитных жидкостях в приближении однородности среды:
, (1)
где 
- напряженность внешнего поля, 
- магнитная восприимчивость магнитной жидкости, 
- объемная концентрация ее дисперсной фазы.
Как следует из [3], полученное выражение для эффективного поля согласуется с формулой Лоренц-Лоренца при выполнении условия
, (2)
которое непосредственно следует из того, что функция Клаузиса-Моссоти не зависит от плотности (концентрации диполей):
(3)
Выражение (1) для эффективного поля может быть представлено в виде 
, т.е. 
, откуда для параметра эффективного поля 
следует:
. (4)
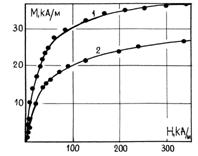
Полученная формула позволяет рассчитать параметр эффективного поля по экспериментально полученной зависимости 
.
Изучение диполь-дипольного взаимодействия однодоменных дисперсных частиц возможно также с помощью анализа температурных зависимостей магнитной восприимчивости магнитных жидкостей. Выражение для расчета эффективного поля можно получить, воспользовавшись подходом, предложенным в [2], возможным благодаря непосредственной связи эффективного поля с действующей на частицу среды силой. При этом, естественно воспользоваться результатами макроскопической теории для объемной плотности сил в магнитном поле. Ранее, выражение для таких сил выводилось во многих работах [3-5] путем приравнивания вариации свободной энергии (при постоянной температуре и векторном потенциале магнитного поля) работе внутренних сил. Вместе с тем авторами работы [6] было показано, что в более общем случае, при вычислении вариации полной (или внутренней) энергии необходимоучитывать вариации температур или энтропий. Если осуществить некоторое виртуальное перемещение элемента магнитной жидкости 
, находящейся в магнитном поле Н (например, в поле соленоида) так, что часть жидкости вытиснится из пространства, занимаемого полем, то изменение энергии поля, соответствующее изотермическому процессу может быть записано в виде, аналогичном выведенного в [3] для жидкого диэлектрика:
, (5)
где 
- концентрация дипольных частиц.
Можно предположить, что в общем случае, с учетом изменения температуры 
это выражение должно быть дополнено слагаемым 
, т.е. 
. Изменение температуры 
определится выражением для магнетокалорического эффекта:
. (6)
Тогда, с учетом предложенного характера виртуального перемещения и выражения для изменения температуры можно получить:
(7)
Наложим ограничение на процесс виртуального перемещения, предположив, что оно не сопровождается изменением концентрации дипольных частиц. В этом случае, второй член в выражении (5) можно положить равным нулю. Тогда, окончательно, для изменения полной энергии с учетом 
получим:
. (8)
Приравняем полученное выражение для 
работе 
пондеромоторных сил, взятой с обратным знаком, т.е. 
. С учетом этого, нетрудно получить:
.
Используя соотношения векторного анализа
,
. (9)
С учетом того, что 
, получим:
. (10)
В работе [2] для плотности сил в дипольном приближении найдено следующее выражение:
(11)
Приравнивая (10) и (11), с учетом отсутствия в МЖ пространственной дисперсии 
и токов проводимости, получим:
(12)
Из формулы (12) видно, что величина эффективного поля связана с магнитной восприимчивостью и ее производной по температуре и может быть рассчитана при использовании зависимости магнитной восприимчивости от температуры. По-видимому, впервые (12) было приведено нами в работе [7] без вывода.
Условие согласуемости (12) с формулой Лоренц-Лоренца для эффективного поля 
имеет вид:
(13)
Соотношение (13) может быть использовано для оценки в случае применимости формулы Лоренц-Лоренца.
Проверим справедливость полученной формулы (12) для некоторых известных функциональных форм зависимости магнитной восприимчивости от температуры.
В случае парамагнитной жидкости для температурной зависимости магнитной восприимчивости справедлив закон Кюри:
и 
(14)
Подставив эти выражения в формулу (12), получим: 
, что и следовало ожидать для системы с невзаимодействующими частицами.
Для парамагнитной жидкости, с магнитной восприимчивостью, подчиняющейся закону Кюри-Вейсса,
, 
, (15)
где 
- температура Кюри. Формула (12) в этом случае дает:
(16)
Приравняв (16) к выражению для эффективного поля, записанного в виде 
и учитывая, что 
, получим:
(17)
Последнее соотношение, с учетом выражения (15) для 
дает 
, что, как известно, следует также непосредственно из закона Кюри-Вейсса. Проведенные оценки позволяют предположить возможность применения формулы (12) для расчета эффективных полей и при других формах зависимости 
, в том случае, когда выполняется поставленное при ее выводе требование однородности среды.
Де Грот С., и Мазур П. Неравновесная термодинамика.- М.: Мир, 1964.-456 с.
Бараш Ю.С. О макроскопическом описании действующего поля в некоторых диэлектриках.// ЖЭТФ.-Т.79, вып.6.-С.2271-2281.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. -М.: Наука.-1982.-623 с.
Стреттон Д. Теория электромагнетизма.- М.-Л.: Гостехиздат, 1948.-312 с.
Пановский В., Филипс М. Классическая электродинамика.- М.: Гостехиздат, 1957.
Гогосов В.В., Налетова В.А., Шапошникова Г.А. Гидродинамика дисперсных систем, взаимодействующих с электромагнитным полем.// Механика жидкости и газа.- №3.-1977.- С.62-70.
Диканский Ю.И. Экспериментальное исследование эффективных полей в магнитной жидкости.// Магнитная гидродинамика.- 1982.- №3. – С.33
Похожие работы
... магнетит в керосине с олеиновой кислотой структурных образований из исперсных частиц. Де Жен и Пинкус [33 МД] рассмотрели коллоид, состоящий из идентичных ферромагнитных частиц, взвешенных в пассивной по отношению к магнитному полю жидкости. Для характеристики дипольного взаимодействия, приводящего к агрегированию использован параметр, называемый константой спаривания . Было предположено, что ...
... возникновением, при некотором пороговом значении напряженности магнитного поля, вытянутых вдоль поля капельных структур авторами [63] связывается обнаруженный ими изгиб на кривой намагничивания магнитной жидкости на основе керосина с объемной концентрацией магнетита Q = 15%. Экспериментальному и теоретическому исследованию каплеподобных агрегатов посвящен ряд работ Бакри и др.[64,65]. В основном, ...
... силы Fy и Fz выражаются аналогичными формулами. ; ; ; . Если ось Х направить вдоль вектора , то . Дипольность обеспечивает частице энергию . В практике исследований проводимости МЖ обычно используют однородное ЭП. Магнитное поле на электрический (неподвижный) заряд не действует, согласно общему выражению для силы Лоренца , где – электрическая и магнитная составляющие. При , и ...
... измерения параметров открывают многообразные пути его применения в промышленности. Внедрению метода ЯМР препятствовали :сложность аппаратуры и ее эксплуатации, высокая стоимость спектрометров, исследовательский характер самого метода. 2.Общая теория ядерного магнитного резонанса. 2.1.Классическое описание условий магнитного резонанса. Вращающийся заряд q можно рассматривать как ...
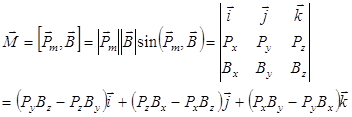
0 комментариев