Навигация
Влияние температуры и магнитного поля на электрическую проводимость и аккумуляцию энергии в кондуктометрической ячейке с магнитной жидкостью
ДИПЛОМНАЯ РАБОТА
Влияние температуры и магнитного поля на электрическую проводимость и аккумуляцию энергии в кондуктометрической ячейкЕ с магнитной жидкостью
Выполнила:
студентка 5 курса ФМФ
отд. «Физика/Математика», группа «В»
Савельева Анна Евгеньевна
Научный руководитель:
кандидат физ.-мат. наук
доц. Полихрониди Н.Г.
Научный консультант:
доц. Баграмян В.А.
План дипломной работы
ВВЕДЕНИЕ................................................................................................................ 3
ГЛАВА I. Обзор литературы..................................................................................... 4
I.1. Аккумуляция энергии в ячейке с МЖ........................................................ 4
I.2. Анизотропия электропроводности МЖ, наведенная внешним воздействием...................................................................................................................... 6
ГЛАВА II. Действие электрического и магнитного полей на структурные элементы МЖ.......................................................................................................... 10
II.1.1. Действие ЭП на свободный заряд........................................................ 10
II.1.2. Действие ЭП на электрический диполь................................................ 10
II.2.1. Действие МП на движущийся заряд.................................................... 13
II.2.2. Действие МП на магнитный диполь..................................................... 15
ГЛАВА III. Математическая теория проводимости МЖ......................................... 16
III.1. Теория проводимости............................................................................. 16
III.2. Влияние ЭП на подвижность МЖ.......................................................... 20
III.3. Влияние МП на подвижность МЖ......................................................... 21
ГЛАВА IV. Результаты эксперимента и их обсуждение.......................................... 24
1. Исследование ВАХ МЖ при разных темпах нагружения ячейки............ 24
2. Влияние температуры на ВАХ МЖ........................................................... 34
3. Исследование разряда и саморазряда КЯ с МЖ...................................... 38
4. Влияние температуры на разряд и саморазряд КЯ с МЖ....................... 51
5. Влияние МП на ВАХ, разряд и саморазряд КЯ с МЖ............................ 56
ВЫВОДЫ И ЗАКЛЮЧЕНИЕ.................................................................................. 59
ЛИТЕРАТУРА........................................................................................................... 60
ВВЕДЕНИЕ
Магнитные жидкости (МЖ) на основе керосина обладают некоторой электрической проводимостью.
Носителями заряда могут быть остаточные ионы технологической процедуры при изготовлении МЖ как продукт распада ионных атмосфер, сопутствующих стабилизирующей оболочке диспергированных частиц и их агрегатов. Предположить в качестве носителей сами магнитные частицы и их агрегата можно, но большая масса и низкая подвижность при, в общем, малом, по-видимому, избыточном заряде маловероятна.
Следствием зависимости могут стать другие явления, уже обнаруженные.
Так уже замечена спонтанная поляризация электродов кондуктометрической ячейки (КЯ), обусловленная, скорее всего, некоторой асимметрией материала электродов. Отчетливо проявляется гистерезис в ходе ВАХ, обусловленный, по-видимому, темпом нагрузки КЯ. Неясна лишь его зависимость от внешних условий, внутреннего состава и структуры МЖ как системы.
Другое замечательное свойство МЖ, связанное с ее проводимостью, – это аккумуляция заряда и энергии в КЯ при ее заряжении. Многие детали этого явления еще скрыты, но кое-что известно определенно. Установлено соотношение (качественное) между заряжающим напряжением и максимальной разностью потенциалов в заряженной КЯ. Изучен ход разряда и найдено, что заряд, накопившийся в ней, значительно превышает заряд этой же ячейки, взятой в роли конденсатора с воздушно-керосиновым и олеиновокислотным наполнителем.
Все эти факты позволили провести первую грубую оценку электрических характеристик МЖ. В настоящей работе продолжены исследования проводимости МЖ на основе керосина и аккумуляции энергии в КЯ в условиях применяющейся температуры; получены некоторые новые результаты о механизме разряда путем изучения саморазряда КЯ и сопоставления его с полным разрядом. Эти результаты пока еще не отличаются высокой степенью точности (количественной) ввиду повышенной чувствительности МЖ к температуре, но качественно определены.
ГЛАВА I. ОБЗОР ЛИТЕРАТУРЫ
I.1. Чеканов В.В., Бондаренко Е.А., Кандаурова Н.В. Накопление заряда в электрофоретической ячейке с МЖ
Были проведены исследования электрических свойств МЖ «магнетит в керосине» с ПАВ, олеиновой кислотой объемной концентрацией 5-12 %.
ВАХ ячейки, используемой в данной работе нелинейны, поэтому ячейку можно представить как конденсатор, накапливающий заряд на обкладках, величина которого оказалась равной 10‑5 Кл(эквивалентная емкость такого конденсатора порядка 10 мкФ.
При подаче на ячейку прямоугольного импульса напряжения с амплитудным значением ± 10 В зависимость напряжения на ячейке от времени имеет вид.
![]()
Получили функцию, вида
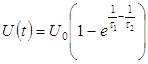 ,
,
где ![]() , C1 – порядка 10 нФ;
, C1 – порядка 10 нФ; ![]() , C2 – порядка 10 мкФ.
, C2 – порядка 10 мкФ.
Оптические исследования показывают, что время применения отражательной способности ячейки при подаче на нее импульсного напряжения и освещении светом длиной волны l = 504 нм, имеет тот же порядок, что и время зарядки конденсатора.
При подаче const напряжения на ячейку в ней течет ток, под действием которого частицы магнетита двигаются к электродам, образуя вблизи поверхностей проводящий слой, отделенный слоем ПАВ. В объеме ячейки образуется объемный заряд, который обуславливает проводимость ячейки.
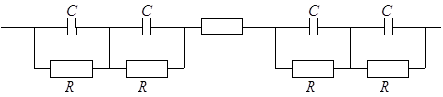
Предполагается, что можно рассматривать ячейку как систему последовательно соединенных конденсаторов, обкладки которых представляют собой проводящий слой диоксида олова, слой проводящих частиц с непроводящим слоем ПАВ, проводящую среду, обусловленную возникновением объемного заряда. Эквивалентная схема ячейки:
 .
.
Используя известные формулы электродинамики, была проведена оценка толщины слоя ПАВ для данной модели. Он оказался порядка 10-50 А, что по порядку величины соответствует толщине ПАВ на коллоидных частицах.
Ячейка обладает нелинейным сопротивлением R, что можно объяснить возникающими в объеме жидкости электрогидродинамическими течениями. В связи с нелинейностью J(U) удалось наблюдать автоколебания тока в схеме с ячейкой.
Полихрониди Н.Г., Кусова А.А. Электро- и магнитно-полевая аккумуляция электрического заряда в ячейке с МЖ
Было проведено исследование эффектов, сопутствующих дрейфу частиц дисперсной фазы, возбужденному течением МЖ типа магнетит в керосине плотностью 1,25 Мг/м3 и проводимостью 100 пСм/м.
В ходе экспериментов пришли к следующему заключению: т.к. МЖ является наследственной системой, то при непрерывном применении действующего на нее фактора последующее состояние зависит от предыдущего, является неравновесным, а равновесие может быть достигнуто с определенным запаздыванием.
Отсюда гистерезис, зависящий от темпа dU/dt наращивания поля при снятии ВАХ. Величина расщепления ВАХ зависит от времени релаксации и текучести МЖ. Поэтому возможен такой подбор темпа, при котором расщепление будет отсутствовать.
Аккумуляция заряда в КЯ под действием ЭП на МЖ может быть объяснена движением и концентрацией массивных комплексов и агрегатов, а также отдельных частиц дисперсной фазы вблизи электродов. Эти скопления сохраняются в течение 10-70 с. При замыкании электродов на нагрузку (измерительный прибор) наблюдается ток разрядки. Природа тока диффузионная. Механизм протекания сложен: внутри ячейки он обусловлен дрейфом ионов, вне – дрейфом электронов, образующими в цепи КЯ единый ток. Закон изменения тока задается процессом диффузии аккумулированных заряженных частиц. Причиной же аккумуляции является электрофорез тяжелых носителей заряда.
Аккумуляция заряда под действием МП на МЖ может быть объяснена как следствие фореза магнитных частиц под действием магнитной силы. Накопление заряда возможно, если перемещаемые частицы обладают адсорбированным зарядом или увлекают вязкостным механизмом другие заряженные микрообъекты.
Была разработана методика использования ВАХ и токов разряда обоих видов для расчета концентраций и подвижностей носителей.
I.2. Кожевников В.М., Ларионов Ю.А. Анизотропия электропроводности дисперсных линейных систем, наведенная внешним воздействием
Чтобы полидисперсность не искажала измеряемые в опытах характеристики частиц, необходимо измерять анизотропию электропроводности дисперсных частиц, ориентируя их полями разной напряженности.
Вектор ориентирующего поля направлен по оси Z. Обозначили изменение электропроводности дисперсной системы, вызванное ориентацией частиц вдоль оси Z, через бкII, а в направлении, перпендикулярном оси – через бкI, где бкII = кII-к, бкI = кI-к.
В тех случаях, когда электропроводности дисперсной системы велики, воздействие ориентирующего поля приведет к ее увеличению за счет джоулева тепла, выделившегося при прохождении тока через дисперсную систему. Эти изменения могут быть сравнимы с измеряемыми величинами бкII и бкI. Однако ошибки при определении бкII и бкI в этом случае будут одинаковыми, и разность бк = бкII-кI исключает данную погрешность, поэтому эта величина исследовалась в данной работе.
Экспериментальные измерения бкII проводились с помощью кюветы, содержащей 4 зонда и 4 электрода. К электродам А и В подводилось воздействующее поле, вдоль оси АВ – направляли вектор МП, электроды С, Д – измерительные. 1-4 – зонды. В области зондов, расстояния между которыми значительно меньше, чем между электродами, ориентирующее и измерительные поля практически однородны. С помощью зондов 1 и 3 можно измерять относительное изменение электропроводности вдоль ориентирующего поля, а с помощью зондов 2 и 4 – относительные изменения электропроводности в перпендикулярном направлении, которые пропорциональны относительному изменению напряжений U13 и U24.
Результаты исследования анизотропии электропроводности МЖ от величины МЖ от величины МП, представлены на рис. 2 (где кривая 1 снята для исходной жидкости, кривая 2 – после воздействия на жидкость ЭП), подтвердили эффективность предложенной методики исследования.
Постановка задачи
Ранее было установлено, что при пропускании электрического тока через КЯ с МЖ в ней накапливается электрический заряд, который можно заметить при разряде КЯ на нагрузку (самописец или измерительный прибор). Как оказалось, разрядный ток подчиняется экспоненциальному закону и по величине тока можно определить электрическую емкость ячейки.
При исследовании ВАХ был обнаружен гистерезисный эффект, который можно объяснить инертностью протекания релаксационных процессов в МЖ. МЖ обладает способностью накапливать заряд под действием ЭП, поэтому возникает запаздывание в уменьшении силы тока при уменьшении величины напряжения, подаваемого на ячейку. Гистерезис наблюдается, если время релаксации МЖ превышает или соизмеримо с периодом наращивания напряжения. Если время релаксации много меньше периода наращивания напряжения, то ВАХ приобретает линейный характер.
При исследовании зависимости пикового значения разности потенциалов на ячейке от продолжительности заряда МЖ было обнаружено существование предельного напряжения – эффект «насыщения» – по величине меньшего, чем напряжение, подаваемое на ячейку от источника питания.
В данной дипломной работе ставятся следующие задачи:
I. 1. Показать возможности переноса заряда теоретическим путем.
2. Действие ЭП на свободные заряды и электрические диполи.
3. Действие МП на магнитный заряд.
II. Снятие ВАХ в задаваемом темпе наращивания напряжения, подаваемого на КЯ, нагреваемую определенной температуры и наблюдение за ходом кривой.
III. 1. Выяснение зависимости пикового значения разрядного тока КЯ с МЖ при ее заряде от продолжительности заряжения, заряжающего напряжения и температуры МЖ в КЯ.
2. Выяснение влияния времени саморазряда ячейки на ход кривой разрядного тока, на величину пикового значения разрядного тока, а также выяснение влияния температуры на время саморазряда (на ход кривой разрядного тока и на его пиковое значение).
IV. Выяснение влияния МП в пределах ![]() на ВАХ КЯ и на кривую разрядного тока.
на ВАХ КЯ и на кривую разрядного тока.
ГЛАВА II. ДЕЙСТВИЕ ПОЛЕЙ
НА СТРУКТУРНЫЕ ЭЛЕМЕНТЫ МАГНИТНОГО КОЛЛОИДА
II.1.1. Действие ЭП на свободный заряд
Одним из непременных элементов МЖ является свободный электрический заряд изначально свободный или появившийся из ионной атмосферы частицы – дисперсной фазы (мицеллы) в результате действия какого-либо фактора. Одним из таких факторов может быть ЭП при пропускании тока. Это поле легко разрушает оболочку эластично связанную с частицей, предварительно вытягивая мицеллу в диполь и отрывая от нее иона, переводя из разряда связанных в свободные. Свободные электрические заряды при наложении на МЖ ЭП подвержены действию этого поля.
Если ЭП вызвано одним точечным зарядом q, величина напряженности поля получается непосредственно из закона Кулона путем деления обеих частей равенства на величину второго заряда:
![]() .
.
Используя закон Кулона в векторной форме запишем напряженность ЭП точечного заряда также в векторной форме:
![]() .
.
Если известна напряженность поля в какой-либо точке, то тем самым определена и сила, действующая на электрический заряд, помещенный в эту точку. А именно:
![]()
![]() ;
;
Кулоновская сила ![]() обуславливает потенциальную энергию W этого поля
обуславливает потенциальную энергию W этого поля ![]()
![]() ,
,
где j – потенциал поля в той точке, где находится в данный момент свободный заряд.
![]() .
.
II.1.2. Действие ЭП на электрический диполь
Наряду со свободными зарядами в магнитном коллоиде существуют электрические диполи, образованные как результат деформации:
а) при прямом действии ЭП; б) при механическом движении в силу действия кулоновских и вязкостных сил.
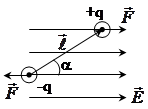 Найдем силу, действующую на диполь в ЭП, причем будем считать сначала, что поле однородно. На концы диполя действуют равные по величине силы
Найдем силу, действующую на диполь в ЭП, причем будем считать сначала, что поле однородно. На концы диполя действуют равные по величине силы ![]() . Эти силы направлены в противоположные стороны и образуют пару сил. Момент M этой пары равен:
. Эти силы направлены в противоположные стороны и образуют пару сил. Момент M этой пары равен:
![]()
где a – угол между вектором ![]() и напряженностью
и напряженностью ![]() поля. Величину
поля. Величину ![]() называют моментом диполя, который является вектором. Он направлен также, как и
называют моментом диполя, который является вектором. Он направлен также, как и ![]() , т.е. от отрицательного заряда к положительному.
, т.е. от отрицательного заряда к положительному.
![]() .
.
Пользуясь понятием момента диполя, можно написать выражение для момента пары сил, действующей на диполь, в виде:
![]() .
.
Направление момента этой пары совпадает с направлением оси вращения диполя, т.е. перпендикулярно к ![]() и
и ![]() .
.
Или же, используя векторную алгебру, можно записать:
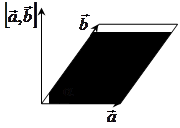
![]()
![]() .
.
В однородном поле на диполь действует только пара сил, которая стремится повернуть диполь таким образом, чтобы ![]() и
и ![]() были параллельны. Для того, чтобы повернуть диполь в ЭП на некоторый угол, нужно совершить определенную работу. Т.к. эта работа равна увеличению потенциальной энергии диполя, то отсюда можно найти выражение для энергии диполя в ЭП. Примем за нуль энергию диполя, перпендикулярного к направлению поля
были параллельны. Для того, чтобы повернуть диполь в ЭП на некоторый угол, нужно совершить определенную работу. Т.к. эта работа равна увеличению потенциальной энергии диполя, то отсюда можно найти выражение для энергии диполя в ЭП. Примем за нуль энергию диполя, перпендикулярного к направлению поля ![]() . Тогда энергия диполя, момент которого составляет угол a с направлением поля, равна
. Тогда энергия диполя, момент которого составляет угол a с направлением поля, равна
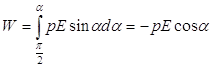 .
.
Рассмотрим теперь диполь в неоднородном поле и положим, что момент диполя параллелен направлению поля ![]() (см. рис.).
(см. рис.).
 Силы, действующие на концы диполя, уже неодинаковы, и поэтому их результирующая ¹ 0. На диполь в неоднородном поле действует сила, стремящаяся передвинуть диполь в область поля с большей напряженностью. Найдем величину той силы. Направим координатную ось X вдоль момента диполя и будем считать, что длина диполя
Силы, действующие на концы диполя, уже неодинаковы, и поэтому их результирующая ¹ 0. На диполь в неоднородном поле действует сила, стремящаяся передвинуть диполь в область поля с большей напряженностью. Найдем величину той силы. Направим координатную ось X вдоль момента диполя и будем считать, что длина диполя ![]() мала (элементарный диполь). Сила, действующая на «-» конец диполя, есть
мала (элементарный диполь). Сила, действующая на «-» конец диполя, есть ![]() , где E – напряженность поля в точке нахождения заряда –q. Сила, действующая на «+» конец диполя, равна
, где E – напряженность поля в точке нахождения заряда –q. Сила, действующая на «+» конец диполя, равна 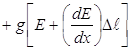 , где
, где ![]() – длина диполя. Поэтому полная сила
– длина диполя. Поэтому полная сила
![]() .
.
В однородном поле ![]() и результирующая сила равна нулю.
и результирующая сила равна нулю.
Если диполь находится в неоднородном поле и не параллелен полю, то на него действуют и пара сил, стремящаяся повернуть диполь параллельно полю, и сила, втягивающая диполь в область более сильного поля.
Пусть ![]() – составляющие напряженности ЭП в прямоугольных осях координат, а
– составляющие напряженности ЭП в прямоугольных осях координат, а ![]() – составляющие момента диполя в тех же осях. Тогда составляющая силы по оси Х равна
– составляющие момента диполя в тех же осях. Тогда составляющая силы по оси Х равна
![]() .
.
Составляющая силы Fy и Fz выражаются аналогичными формулами.
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Если ось Х направить вдоль вектора ![]() , то
, то
![]() .
.
Дипольность обеспечивает частице энергию ![]()
![]() .
.
В практике исследований проводимости МЖ обычно используют однородное ЭП.
Магнитное поле на электрический (неподвижный) заряд не действует, согласно общему выражению для силы Лоренца
![]() ,
,
где ![]() – электрическая и магнитная составляющие.
– электрическая и магнитная составляющие.
При ![]() ,
, ![]() и тогда
и тогда ![]() . Если же
. Если же ![]() , то даже при
, то даже при ![]()
![]() .
.
Т.к. тепловое движение хаотично, то действие силы Лоренца на МЖ в среднем никак не ощущается, поскольку ионы-носители заряда являются частицами замкнутой системы. Небеспорядочной скоростью могут обладать носители в дрейфе (ток) или в едином гидродинамическом потоке. Тогда сила Лоренца подействует на каждую частицу одинаково и вся система носителей должна сдвинуться. При этом часть носителей будет увеличена из потока и уменьшить ток.
II.2.1. Действие магнитного поля на движущийся заряд
Каждый проводник с током создает в пространстве МП. Но электрический ток в проводнике есть движение заряженных частиц: в металлах – это движение е-, в электролитах – ионов, в газовом разряде – и ионов, и е-. Отсюда можно заключить, что всякий движущийся заряд создает вокруг себя МП. Найдем величину этого поля.
Рассмотрим малый отрезок провода длиной l с током i. Этот отрезок создает в некоторой точке, удаленной на расстояние r, напряженность поля
![]() .
.
Но силу тока можно выразить через плотность тока j и сечение провода ![]() , а плотность тока – через концентрацию заряженных частиц n и их скорость
, а плотность тока – через концентрацию заряженных частиц n и их скорость ![]() . Это дает
. Это дает ![]() , где N – полное число частиц в отрезке провода. Напряженность поля можно представить в виде
, где N – полное число частиц в отрезке провода. Напряженность поля можно представить в виде ![]() .
.
Напряженность поля, вызываемого одной заряженной частицей, имеет значение
![]() .
.
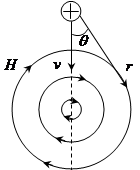 Направление этого поля перпендикулярно к скорости v частиц и к радиусу – вектору r, проведенному из заряда в рассматриваемую точку, и подчиняется правилу правого буравчика. Используя обозначение векторной алгебры
Направление этого поля перпендикулярно к скорости v частиц и к радиусу – вектору r, проведенному из заряда в рассматриваемую точку, и подчиняется правилу правого буравчика. Используя обозначение векторной алгебры
![]() .
.
Эта формула выражает напряженность поля «+» заряда, движущегося со скоростью v. Если движется «-» заряд, то в формуле нужно заменить е на -е.
Движущийся заряд по своим магнитным действиям эквивалентен элементу тока ![]() . В этих формулах v – относительная скорость, т.е. скорость относительно наблюдателя и тех приборов, которые измеряют МП.
. В этих формулах v – относительная скорость, т.е. скорость относительно наблюдателя и тех приборов, которые измеряют МП.
Т.к. всякий ток есть движение заряженных частиц, следовательно, на движущийся заряд в МП действует сила. Определим величину этой силы. На провод длиной l с током i действует сила ![]() , где B – магнитная индукция. С другой стороны
, где B – магнитная индукция. С другой стороны ![]() , где N – полное число движущихся заряженных частиц внутри провода. Учитывая, что направление
, где N – полное число движущихся заряженных частиц внутри провода. Учитывая, что направление ![]() совпадает с направлением скорости
совпадает с направлением скорости ![]() движения «+» частиц (с направлением тока), можно выражение для силы представить в виде:
движения «+» частиц (с направлением тока), можно выражение для силы представить в виде:
![]() .
.
Сила, действующая на провод, пропорциональна полному числу движущихся частиц, а значит, сила, действующая на одну частицу, равна
![]() .
.
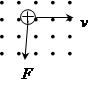 Направление этой силы перпендикулярно к направлению скорости v и магнитной индукции B и подчиняется правилу правого буравчика (см. рис.).
Направление этой силы перпендикулярно к направлению скорости v и магнитной индукции B и подчиняется правилу правого буравчика (см. рис.).
Полученный результат можно выразить в виде векторной формулы
![]() .
.
Если имеется еще ЭП, то полная сила равна
![]() .
.
Эту силу, действующую на движущийся заряд, называют силой Лоренца.
Эта формула получена на основе анализа опытных данных о взаимодействии неподвижных контуров с током. Поэтому скорость v в формуле есть скорость относительно МП.
Сила Лоренца проявляется при движении е- и ионов в МП.
II.2.2. Действие МП на магнитный диполь
Другим, определяющим специфичность МЖ, структурным эффектом является магнитный диполь – микрокристаллический агрегат в коллоидной частице. В измерениях с участием МП используются однородные и неоднородные поля. Действие этих полей на магнитный диполь аналогично действию ЭП на электрический диполь.
Действительно, пусть магнитный диполь ![]() помещен в произвольное МП
помещен в произвольное МП ![]() , тогда на него действует механический момент:
, тогда на него действует механический момент:
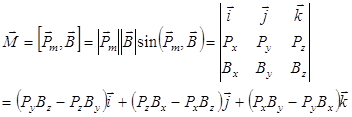 .
.
Выражение упростим, если поле будет однородным, т.к. система координат может быть выбрана так, чтобы ![]() или
или ![]() , или оба вектора совпадали с одной (двумя) осями координат. Энергия диполя просто задается формулой
, или оба вектора совпадали с одной (двумя) осями координат. Энергия диполя просто задается формулой ![]() . Магнитный диполь в случае действия на него неоднородного МП
. Магнитный диполь в случае действия на него неоднородного МП ![]() подвержен действию магнитной силы:
подвержен действию магнитной силы:
![]() .
.
Так как в местах расположения магнитных диполей токи, образующие поле отсутствуют, то ![]() , но тогда
, но тогда
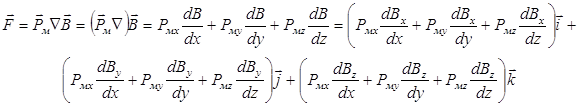
В однородном МП все производные равны нулю, следовательно, ![]() . Поэтому МЖ должна подвергнута действию ИМП. Наибольшее влияние на дрейф будет достигнуто, если сила
. Поэтому МЖ должна подвергнута действию ИМП. Наибольшее влияние на дрейф будет достигнуто, если сила ![]() (т.к. другой упорядочивающей скорости нет). Следовательно,
(т.к. другой упорядочивающей скорости нет). Следовательно, ![]() должна быть коллинеарна напряженности ЭП, создающего ток.
должна быть коллинеарна напряженности ЭП, создающего ток.
Пусть ![]() , тогда
, тогда ![]() или
или ![]() . Это возможно, если
. Это возможно, если ![]() , т.е. когда
, т.е. когда ![]() и
и ![]() .
.
В этом случае ![]() . Эта сила будет вытягивать диаполи при благоприятной их ориентации до полной минимизации магнитной поступательной энергии. Поле такого рода однонаправлено, но неоднородно из-за различной густоты магнитных силовых линий. Такое поле может быть создано при помощи полосового постоянного магнетита вблизи его полюсов, площадь сечения которых заметно больше площади КЯ, или с помощью соленоида с теми же габаритами.
. Эта сила будет вытягивать диаполи при благоприятной их ориентации до полной минимизации магнитной поступательной энергии. Поле такого рода однонаправлено, но неоднородно из-за различной густоты магнитных силовых линий. Такое поле может быть создано при помощи полосового постоянного магнетита вблизи его полюсов, площадь сечения которых заметно больше площади КЯ, или с помощью соленоида с теми же габаритами.
ГЛАВА III. Математическая теория проводимости МЖ
III.1. Теория проводимости
Плотность тока дрейфа под действием кулоновского поля в любой момент времени определяется выражением (при одном знаке носителей):
![]() ,
,
где g – заряд отдельного носителя, n – концентрация носителей, vдр – скорость дрейфа.
В более общем случае для двух носителей ![]() , где знаки «+» и «-» относятся к положительным и отрицательным носителям соответственно.
, где знаки «+» и «-» относятся к положительным и отрицательным носителям соответственно.
Т.к. ![]() , (m – подвижность), то
, (m – подвижность), то ![]() , считая, что
, считая, что ![]() , и что
, и что ![]() , то
, то ![]() , где s - коэффициент электропроводимости.
, где s - коэффициент электропроводимости.
Наряду с током, обусловленным дрейфом, возникает диффузионный ток с плотностью
![]() ,
,
где rз – объемная плотность заряда, равная gn, D – коэффициент диффузии, определяемый соотношением Нернста-Эйнштейна.
![]() ,
,
тогда полный ток составит (в случае носителей одного знака)
![]() ;
;
![]() .
.
При условии продолжительного действия поля E наступает динамическое равновесие, при котором ![]() :
:
![]() .
.
Отсюда нетрудно получить с учетом ![]() для одномерного случая
для одномерного случая ![]() , что
, что
![]() или
или ![]() .
.
После интегрирования можно получить
![]()
здесь ![]() – значение r при
– значение r при ![]() .
.
Разделение носителей заряда неоднородно ввиду различия их состава, массы, подвижности. Поэтому и m, и E являются функциями координат. Среднее значение плотности тока по толщине кондуктометрической ячейки КЯ вдоль оси ОХ, перпендикулярной площади электродов будет
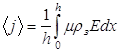 ,
,
причем, согласно уравнению Пуассона
![]()
для одномерного случая ![]() .
.
Если в КЯ находятся и свободные и связанные (фиксированные) заряды rсв и rсвяз, то
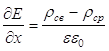 ,
,
отсюда ![]() .
.
Тогда, считая для простоты ![]() , можно записать:
, можно записать:
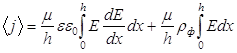 .
.
Пусть граничными условиями будут:
1. при ![]()
![]() ;
;
2. при ![]()
![]() ,
,
тогда, так как
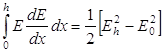
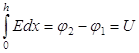 ,
,
![]() – приращение потенциала, то
– приращение потенциала, то
![]() .
.
Это выражение можно преобразовать
![]() ,
,
![]() – суммарное поле внутри КЯ. Это легко связать с поверхностной плотностью s* зарядов обоих типов
– суммарное поле внутри КЯ. Это легко связать с поверхностной плотностью s* зарядов обоих типов ![]() .
.
В то же время ![]() учтя это, можно получить
учтя это, можно получить
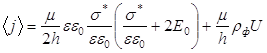
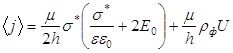
Поведение ![]() можно оценить по ее производной. Пусть
можно оценить по ее производной. Пусть ![]() , тогда
, тогда ![]() и
и ![]()
![]() .
.
При этом МЖ должна быть нейтральной. Пусть полный заряд ![]()
Тогда ![]() ,
, ![]() по модулю.
по модулю.
Но тогда ![]() и
и ![]() .
.
 Т.к.
Т.к. ![]() и
и ![]() , где v – объем КЯ и
, где v – объем КЯ и ![]() , S – площадь, то
, S – площадь, то ![]() , т.к.
, т.к. 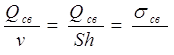 , а
, а ![]() , тогда
, тогда ![]() .
.
![]() .
.
Это линейная функция, где C¢ имеет смысл удельной электропроводности s. Следовательно, если ток протекает, то он должен подчиняться закону Ома (см. рис.).
Перенос электрического заряда в КЯ при пропускании электрического тока
Прохождение тока через КЯ как механизм кинетический (наличие градиента, определяющего перенос градиента потенциала ![]() ) не может быть ясен без детального изучения участников переноса и их характеристик – заряда, подвижности, концентрации. Хоты МЖ должна быть в идеале изолятором, она содержит некоторое количество ионов остаточных атомов технологического процесса. Размеры, форма и концентрация диспергированных магнитных частиц в МЖ, их электрическая оболочка и среда, в которой они взвешены, каждая по своему влияют на электрофизические характеристики МЖ и на ее проводимость в целом.
) не может быть ясен без детального изучения участников переноса и их характеристик – заряда, подвижности, концентрации. Хоты МЖ должна быть в идеале изолятором, она содержит некоторое количество ионов остаточных атомов технологического процесса. Размеры, форма и концентрация диспергированных магнитных частиц в МЖ, их электрическая оболочка и среда, в которой они взвешены, каждая по своему влияют на электрофизические характеристики МЖ и на ее проводимость в целом.
Поставленные соответствующим образом эксперименты посвящены выяснению роли магнитных частиц в процессе протекания тока через МЖ.
Носителями заряда частицы становятся в случае адсорбции или деадсорбции на их электрической оболочке ионов обоих знаков атомов технологического процесса, в том числе и остаточных. Их дрейф в ЭП описывается следующим динамическим уравнением движения:
![]() .
.
Это движение считается установившимся и поэтому ![]() . Тогда
. Тогда ![]() и в проекции на направление скорости дрейфа имеем:
и в проекции на направление скорости дрейфа имеем:
![]()
Fс – стоксово сопротивление сферической частицы радиуса r в среде с вязкостью h. Подвижность этих носителей равна
![]() ,
,
где ![]() – скорость дрейфа магнитной частицы, E – напряженность ЭП.
– скорость дрейфа магнитной частицы, E – напряженность ЭП.
Чем больше заряд и чем меньше размеры частицы и вязкость среды, тем больше подвижность и наоборот. Концентрация магнитных частиц, обладающих электрическим зарядом, зависит от соответствующей дисперсной фазы и является равновесной величиной, характерной для каждого состояния. Магнитные частицы могут быть увлечены силами вязкого трения даже, если не имеют электрического заряда и, поэтому, не подвержены действию кулоновских сил. Это их взаимодействие с немагнитными носителями тока приводит к значительному уменьшению подвижностей ионов и комплексов.
III.2. Влияние электрического поля на подвижность МЖ
Рассмотрим влияние приложения кулоновского поля на подвижность носителей заряда.
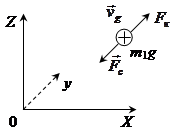
![]() – кулоновские силы, создаваемые полем
– кулоновские силы, создаваемые полем ![]() ,
, ![]() – сила сопротивления.
– сила сопротивления.
Носитель массой m и зарядом q обладает скоростью дрейфа ![]() . Тогда для динамического уравнения движения
. Тогда для динамического уравнения движения ![]() имеем
имеем
![]() .
.
Пусть ![]() ,
, ![]() – коэффициент сопротивления.
– коэффициент сопротивления.
Тогда ![]() , т.к.
, т.к. ![]() и
и ![]() сонаправлены и
сонаправлены и ![]() , то
, то
![]()
![]() .
.
Обозначим ![]() ,
, ![]() , тогда
, тогда
![]() .
.
Это дифференциальное уравнение первого порядка с постоянными коэффициентами, линейное, неоднородное. Его решение получится из решения соответствующего однородного уравнения:
![]() .
.
Решение этого уравнения ![]()
![]() ,
,
считая ![]() неизвестным и дифференцируя по времени t, получим
неизвестным и дифференцируя по времени t, получим
![]() .
.
Поставив это в неоднородное уравнение, получим
![]()
![]()
![]() .
.
Тогда ![]() .
.
Так как подвижность определяется по скорости дрейфа, то
![]() .
.
Следовательно, m от напряженности поля не должно зависеть.
III.3. Влияние МП на подвижность носителей в МЖ
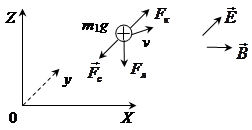 Рассмотрим влияние МП на концентрацию и подвижность носителей
Рассмотрим влияние МП на концентрацию и подвижность носителей
Динамическое уравнение движения в этом случае
![]() ,
,
![]() – сила Лоренца.
– сила Лоренца.
Скорость дрейфа ![]() имеет направление
имеет направление ![]() , если нет МП
, если нет МП ![]() . В этом случае составляющие скорости, вообще говоря, ненулевые.
. В этом случае составляющие скорости, вообще говоря, ненулевые.
Представим уравнение движения в декартовых координатах. Выберем направление осей как это показано на рисунке, учитывая, что ![]() ,
, ![]() ,
, ![]() .
.
Представим уравнение движения следующим образом:
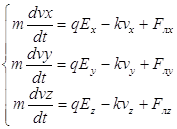
при данном выборе осей ![]() ,
, ![]() .
.
Сила Лоренца
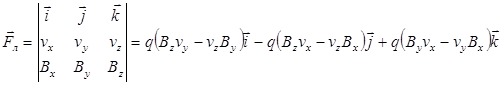 .
.
При данном выборе осей
С помощью ранее разработанной методики была снята ВАХ для МЖ. Исследована зависимость ВАХ от темпа нагружения КЯ ( скорости изменения величины подаваемого напряжения )
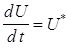 .
.
Получены следующие результаты :
0 комментариев