Введение
1. Спектральный анализ и спектральный синтез периодических сигналов
1.1 Синтез периодических сигналов
1.2 Анализ периодических сигналов
2.Численные методы расчетов спектральных и временных характеристик периодических сигналов
2.1 Численные методы расчетов временных характеристик
2.2.Численные методы расчетов частотных характеристик
Выводы
Литература
Введение:Известно , что периодическое несинусоидальное колебание можно представить бесконечным тригонометрическим рядом Фурье, который в общем случае содержит постоянную и гармонические составляющие .
Часто используется следующая форма математической записи ряда Фурье:
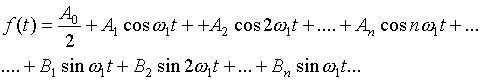
где f(t)-функция, раскладываемая в ряд,
, а 
- частота следования импульсов.
Коэффициенты ряда определяются следующими выражениями:
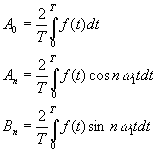(1)
где 
=1,2,3…M соответственно функции(1.2),(1.3),(1.4)
Здесь А - постоянная составляющая , An и Bn - амплитуды косинусной и синусной составляющих, Т- период повторения сигнала , М- число гармоник,
n – номер гармоник. Ряд (1) можно преобразовать к более удобному виду:
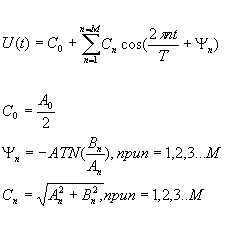(2)
Здесь 
-постоянная составляющая, 
-амплитуда n-ой гармоники,
-фаза n-ой гармоники. Формула (2.1) используется при спектральном анализе и синтезе периодических сигналов.
Сигнал задан в виде набора спектральных составляющих: Cn – амплитуда,- частота,
начальная фаза n- ой гармоники. Здесь n=1,2,…,M- номер гармоники , M- число гармоник в спектре сигналов. Требуется осуществить синтез сигнала U(t) и построить его временную диаграмму. Задача синтеза сигнала заключается в расчёте временной функции сигнала U(t) по известному спектру сигнала. При этом спектр сигнала задан в виде таблицы амплитуд, частот и фаз гармоник. Задача синтеза сигнала решается путём расчёта значений функции во временной области U(t)
Численный синтез осуществляется путём расчёта отсчетов сигнала через равные интервалы времени и построения временной диаграммы сигнала. При этом интервал времени между соседними отсчётами называют интервалом дискретизации.
1.2СПЕКТРАЛЬНЫЙ АНАЛИЗ ПЕРИОДИЧЕСКИХ СИГНАЛОВ:Задача анализа сигнала заключается в расчёте его спектра, т.е. амплитуд, частот, фаз и гармоник. При этом сигнал задан в виде функции времени U(t) . Задача анализа решается путём расчёта амплитудно-частотных Cn=f(w) и фазочастотных =f(w) характеристик.
Сигнал задан в виде функции времени U(t) , повторяющийся с периодом Т. Требуется выполнить спектральный анализ сигнала и построить графики амплитудного и фазового спектров сигнала.
2.Численные методы расчетов спектральных и временных характеристик периодических сигналовДля расчета спектральных и временных характеристик периодического сигнала используем численные методы, чтобы упростить и автоматизировать задачу
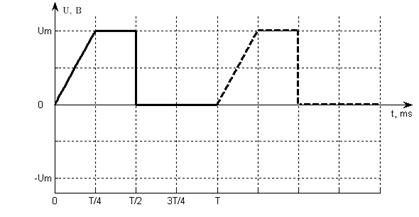
Дан сигнал:
Дана таблица параметров данного сигнала
| U, mv | M | t0,mks | T,mks | r |
| 2.8 | 10 | 459 | 1499 | 2 |
U(t) – функция времени, описывающая сигнал;
M – число учитываемых гармоник;
U- амплитуда;
T - текущее время;
t0 – время задержки сигнала;
T – период частоты повторения первой гармоники;
r – постоянный коэффициент
2.1 ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТОВВРЕМЕННЫХ ХАРАКТЕРИСТИКЧисленный синтез осуществляется путём расчёта отсчётов сигнала через равные интервалы времени и построения временной диаграммы сигнала. При этом интервал времени между соседними отсчётами называют интервалом дискретизации.
Интервал дискретизации Тд вычисляем по формуле ТД<T/(к * M),где k=5(т. к на периоде наибольшей частоты в спектре сигнала должно размещаться не менее 5 отсчетов)
Интервал времени Тс равен Tmax и равен 50 т. к k*M=50(k=5,M=10). Исходя из формулы, интервал дискретизации Тд равен Тд=Т/(k*М), Тд=29,98
| M=10 | K=5 | t0=459 | U0=2,8 | T=1499 |
Исходя из полученных данных, строим таблицу
| t | u(1) | u(2) | u(3) | u(4) | u(5) | u(6) | u(7) | u(8) | u(9) | u(10) | SUM |
| 0 | 0,965808 | 0,812595 | 0,549919 | 0,250406 | -0,00868 | -0,17017 | -0,21345 | -0,15715 | -0,0481 | 0,058467 | 2,039651 |
| 29,98 | 0,62897 | 0,586654 | 0,507145 | 0,399954 | 0,277617 | 0,15392 | 0,041996 | -0,04743 | -0,10736 | -0,13529 | 2,306171 |
| 59,96 | 0,282224 | 0,278401 | 0,270848 | 0,259749 | 0,245373 | 0,228066 | 0,208243 | 0,186371 | 0,162963 | 0,138557 | 2,260794 |
| 89,94 | -0,06897 | -0,06891 | -0,0688 | -0,06863 | -0,06841 | -0,06814 | -0,0678 | -0,06742 | -0,06698 | -0,06649 | -0,68055 |
| 119,92 | -0,41908 | -0,40656 | -0,3822 | -0,3473 | -0,3037 | -0,25369 | -0,19984 | -0,14483 | -0,09131 | -0,04174 | -2,59023 |
| 149,9 | -0,76258 | -0,68716 | -0,54975 | -0,37435 | -0,19052 | -0,02729 | 0,092569 | 0,156662 | 0,164662 | 0,127265 | -2,0505 |
| 179,88 | -1,09407 | -0,87135 | -0,50752 | -0,1302 | 0,141263 | 0,24343 | 0,188368 | 0,04829 | -0,08485 | -0,1436 | -2,21024 |
| 209,86 | -1,40832 | -0,93328 | -0,27163 | 0,208272 | 0,310962 | 0,118853 | -0,11591 | -0,18642 | -0,07389 | 0,081852 | -2,26951 |
| 239,84 | -1,70039 | -0,86427 | 0,067917 | 0,395863 | 0,123862 | -0,19872 | -0,174 | 0,066585 | 0,163896 | 0,024397 | -2,09487 |
| 269,82 | -1,96566 | -0,674 | 0,381545 | 0,296665 | -0,20536 | -0,1936 | 0,137477 | 0,145388 | -0,10145 | -0,11738 | -2,29638 |
| 299,8 | -2,19997 | -0,38916 | 0,549579 | -0,01746 | -0,29895 | 0,125904 | 0,156966 | -0,15618 | -0,05536 | 0,146543 | -2,13808 |
| 329,78 | -2,39962 | -0,04971 | 0,507898 | -0,31893 | -0,04953 | 0,240959 | -0,15693 | -0,04915 | 0,160677 | -0,09603 | -2,21036 |
| 359,76 | -2,56146 | 0,296704 | 0,272408 | -0,38935 | 0,256724 | -0,03527 | -0,13752 | 0,186463 | -0,11654 | -0,0067 | -2,23455 |
| 389,74 | -2,68295 | 0,601491 | -0,06703 | -0,1777 | 0,268408 | -0,25422 | 0,173972 | -0,06575 | -0,036 | 0,105786 | -2,13401 |
| 419,72 | -2,76217 | 0,821886 | -0,38089 | 0,162689 | -0,02788 | -0,06035 | 0,115958 | -0,14595 | 0,155054 | -0,14735 | -2,26901 |
| 449,7 | -2,79788 | 0,926965 | -0,54941 | 0,385215 | -0,29218 | 0,231523 | -0,18834 | 0,155685 | -0,12988 | 0,108799 | -2,14949 |
| 479,68 | -2,7895 | 0,901985 | -0,50827 | 0,328667 | -0,22123 | 0,147439 | -0,09262 | 0,05001 | -0,01611 | -0,01109 | -2,21071 |
| 509,66 | -2,73717 | 0,75045 | -0,27319 | 0,034011 | 0,10356 | -0,17607 | 0,19982 | -0,1865 | 0,14711 | -0,09265 | -2,23063 |
| 539,64 | -2,64173 | 0,493623 | 0,066146 | -0,28528 | 0,309524 | -0,21366 | 0,067854 | 0,064915 | -0,14127 | 0,146013 | -2,13387 |
| 569,62 | -2,50466 | 0,167537 | 0,380238 | -0,3979 | 0,160339 | 0,095698 | -0,20823 | 0,1465 | 0,004029 | -0,11999 | -2,27643 |
| 599,6 | -2,32813 | -0,18206 | 0,549234 | -0,22225 | -0,17282 | 0,24966 | -0,04205 | -0,15519 | 0,136964 | 0,028721 | -2,13792 |
| 629,58 | -2,11493 | -0,5061 | 0,508647 | 0,11441 | -0,30768 | -0,00179 | 0,21344 | -0,05087 | -0,15056 | 0,078161 | -2,21727 |
| 659,56 | -1,8684 | -0,75914 | 0,273965 | 0,368187 | -0,08951 | -0,25033 | 0,015597 | 0,186538 | 0,024105 | -0,14254 | -2,24154 |
| 689,54 | -1,59244 | -0,90567 | -0,06526 | 0,355225 | 0,231368 | -0,09237 | -0,21537 | -0,06408 | 0,124769 | 0,129424 | -2,0944 |
| 719,52 | -1,29139 | -0,92513 | -0,37958 | 0,084915 | 0,286774 | 0,21559 | 0,011093 | -0,14705 | -0,15759 | -0,04593 | -2,34829 |
| 749,5 | -0,96999 | -0,81478 | -0,54906 | -0,24691 | 0,013135 | 0,173461 | 0,213998 | 0,154694 | 0,04382 | -0,06253 | -2,04417 |
| 779,48 | -0,63332 | -0,59012 | -0,50902 | -0,39986 | -0,27558 | -0,15034 | -0,03761 | 0,051727 | 0,110706 | 0,136999 | -2,29641 |
| 809,46 | -0,28666 | -0,28265 | -0,27474 | -0,26312 | -0,24809 | -0,23001 | -0,20934 | -0,18657 | -0,16226 | -0,13698 | -2,28042 |
| 839,44 | 0,064511 | 0,064465 | 0,064374 | 0,064237 | 0,064055 | 0,063828 | 0,063556 | 0,06324 | 0,06288 | 0,062476 | 0,637623 |
| 869,42 | 0,414666 | 0,40254 | 0,378926 | 0,345061 | 0,302703 | 0,25402 | 0,20146 | 0,147599 | 0,094986 | 0,045993 | 2,587955 |
| 899,4 | 0,758288 | 0,684135 | 0,548883 | 0,3759 | 0,194028 | 0,031719 | -0,08852 | -0,15419 | -0,1645 | -0,12945 | 2,056285 |
| 929,38 | 1,089963 | 0,869742 | 0,509391 | 0,134413 | -0,13728 | -0,24209 | -0,19049 | -0,05258 | 0,080998 | 0,142529 | 2,204598 |
| 959,36 | 1,404466 | 0,933319 | 0,275519 | -0,20445 | -0,31107 | -0,12278 | 0,11213 | 0,186595 | 0,077844 | -0,07811 | 2,273469 |
| 989,34 | 1,696843 | 0,865945 | -0,06349 | -0,3952 | -0,12794 | 0,195908 | 0,176594 | -0,0624 | -0,16428 | -0,02878 | 2,093202 |
| 1019,32 | 1,962486 | 0,677074 | -0,37827 | -0,29964 | 0,201987 | 0,196467 | -0,13401 | -0,14814 | 0,097904 | 0,120023 | 2,295876 |
| 1049,3 | 2,197212 | 0,393204 | -0,54871 | 0,013 | 0,300154 | -0,12201 | -0,15999 | 0,153688 | 0,059538 | -0,146 | 2,140091 |
| 1079,28 | 2,39732 | 0,054166 | -0,50976 | 0,31622 | 0,053923 | -0,24236 | 0,153841 | 0,053438 | -0,1616 | 0,0926 | 2,20779 |
| 1109,26 | 2,55966 | -0,29247 | -0,2763 | 0,390349 | -0,25418 | 0,030848 | 0,14092 | -0,18662 | 0,113344 | 0,011153 | 2,236711 |
| 1139,24 | 2,681674 | -0,59807 | 0,062602 | 0,181684 | -0,27063 | 0,253962 | -0,17131 | 0,061559 | 0,04034 | -0,10884 | 2,132964 |
| 1169,22 | 2,761439 | -0,81976 | 0,377611 | -0,1586 | 0,023437 | 0,064677 | -0,11969 | 0,148684 | -0,1565 | 0,147351 | 2,268639 |
| 1199,2 | 2,797698 | -0,92643 | 0,548527 | -0,38399 | 0,290617 | -0,22963 | 0,186138 | -0,15318 | 0,127089 | -0,10574 | 2,151087 |
| 1229,18 | 2,78988 | -0,90312 | 0,510129 | -0,33119 | 0,224342 | -0,15105 | 0,096623 | -0,05429 | 0,020539 | 0,006639 | 2,2085 |
| 1259,16 | 2,738109 | -0,75309 | 0,277071 | -0,03845 | -0,09934 | 0,172818 | -0,19811 | 0,186636 | -0,14906 | 0,096074 | 2,232645 |
| 1289,14 | 2,6432 | -0,4974 | -0,06172 | 0,282141 | -0,30904 | 0,216055 | -0,07207 | -0,06072 | 0,138931 | -0,14655 | 2,132831 |
| 1319,12 | 2,506649 | -0,17192 | -0,37695 | 0,398333 | -0,16414 | -0,09155 | 0,207044 | -0,14922 | 0,00043 | 0,117343 | 2,276008 |
| 1349,1 | 2,330606 | 0,177679 | -0,54835 | 0,225947 | 0,169094 | -0,25049 | 0,046413 | 0,152669 | -0,13939 | -0,02433 | 2,139844 |
| 1379,08 | 2,117845 | 0,502351 | -0,5105 | -0,11013 | 0,308313 | -0,00267 | -0,2128 | 0,055145 | 0,148694 | -0,0819 | 2,214352 |
| 1409,06 | 1,871719 | 0,75654 | -0,27785 | -0,36642 | 0,093773 | 0,249488 | -0,02004 | -0,18665 | -0,01969 | 0,143611 | 2,244486 |
| 1439,04 | 1,596104 | 0,904582 | 0,060829 | -0,35725 | -0,22836 | 0,09651 | 0,21528 | 0,059872 | -0,12763 | -0,12723 | 2,092694 |
| 1469,02 | 1,295343 | 0,925705 | 0,376292 | -0,08927 | -0,28847 | -0,21319 | -0,00664 | 0,149756 | 0,156231 | 0,041675 | 2,347436 |
| 1499 | 0,974174 | 0,816945 | 0,548165 | 0,24339 | -0,01759 | -0,1767 | -0,21446 | -0,15215 | -0,03951 | 0,066542 | 2,048811 |
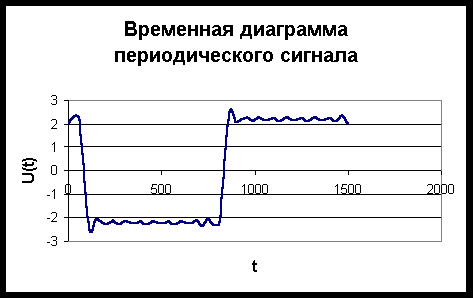
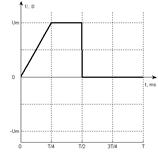
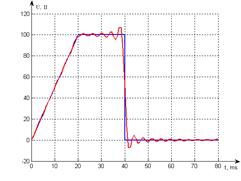
После расчета строим временную диаграмму сигнала
2.2.ЧИСЛЕННЫЕ МЕТОДЫ РАСЧЕТОВ ЧАСТОТНЫХ ХАРАКТЕРИСТИКДля того чтобы определить амплитудно-частотную и фазочастотную характеристику периодического сигнала представим сигнал в виде ряда Фурье (2). Коэффициенты ряда Аn и Bn определяются по формулам (1) . Для того чтобы вычислить An и Bn преобразуем интеграл к сумме, а непрерывную функцию U(t) представим как дискретную (t1) , где tI=i*TД (ТД – интервал дискретизации).
Представим непрерывную функцию U(t) как дискретную, сделав замену t i * ТД и di ТД, преобразуем выражения An ,Bn и запишем ряд Фурье в окончательном виде: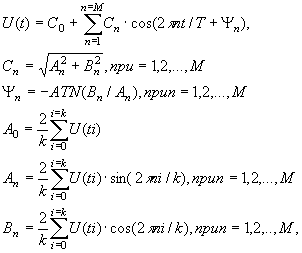
( 5)
где k=T/ТД – число отсчётов сигнала на интервале T. Интервал дискретизации ТД выбираем таким, чтобы на самом крутом участке функции U(t) , было не менее 5 отсчётов, либо не менее 5 отсчётов на периоде наибольшей частоты в спектре сигнала. Исходя из формулы(5),вычисляем амплитудно-частотную и фазочастотную характеристики. Расчеты приведены в таблице
| i | Wn | U(ti) | A0 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 0 | 0 | 2,03965 | 0,81586 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 4189,46 | -2,1380 | -0,0394 | -0,0374 | -0,0232 | 0,0230 | 0,03747 | 0,00013 | -0,0374 | -0,0233 | 0,0229 | 0,0375 | 0,00025 |
| 2 | 8378,92 | -2,1379 | -0,89454 | -0,52672 | 0,851458 | -0,8496 | 0,522101 | 0,005699 | -0,53131 | 0,85318 | -0,84789 | 0,51746 | 0,011397 |
| 3 | 12568,4 | 2,05628 | -0,07202 | 0,042223 | -0,06841 | 0,06862 | -0,04278 | 0,000688 | 0,04166 | -0,06819 | 0,06883 | -0,04333 | 0,001376 |
| 4 | 16757,8 | 2,15108 | 0,788411 | -0,75044 | -0,46016 | 0,46827 | 0,747301 | -0,01005 | -0,75346 | -0,45197 | 0,47632 | 0,74403 | -0,02009 |
| 5 | 20947,3 | 2,04881 | 1,607935 | -0,00512 | -0,01024 | -0,0153 | -0,02049 | -0,02561 | -0,03073 | -0,03585 | -0,04097 | -0,04609 | -0,05121 |
| i | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B9 | B10 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | -0,0122 | 0,03182 | 0,0319 | -0,0121 | -0,0394 | -0,0123 | 0,03175 | 0,03197 | -0,012 | -0,0394 |
| 2 | 0,723026 | -0,27426 | -0,27968 | 0,726367 | -0,89452 | 0,719656 | -0,26883 | -0,28508 | 0,729678 | -0,89447 |
| 3 | 0,058349 | -0,02252 | -0,02186 | 0,057943 | -0,07202 | 0,05875 | -0,02317 | -0,02121 | 0,057532 | -0,07201 |
| 4 | 0,241721 | -0,64019 | -0,63428 | 0,251263 | 0,788347 | 0,23214 | -0,646 | -0,62826 | 0,260763 | 0,788155 |
| 5 | 1,607927 | 1,607903 | 1,607862 | 1,607805 | 1,607732 | 1,607642 | 1,607536 | 1,607413 | 1,607275 | 1,60712 |
| An | Bn | Cn | Fn |
| -1,27749 | 2,618833 | 2,913808 | 1,116948 |
| 0,28946 | 0,702756 | 0,760035 | -1,18008 |
| -0,30507 | 0,70394 | 0,767204 | 1,161849 |
| 1,243611 | 2,631307 | 2,910385 | -1,12929 |
| -0,02914 | 1,390168 | 1,390474 | 1,549838 |
| -1,31124 | 2,605878 | 2,91718 | 1,104605 |
| 0,273895 | 0,701282 | 0,752871 | -1,19845 |
| -0,32073 | 0,704832 | 0,774375 | 1,143753 |
| 1,209595 | 2,643297 | 2,906912 | -1,14163 |
| -0,05827 | 1,389429 | 1,390651 | 1,528881 |
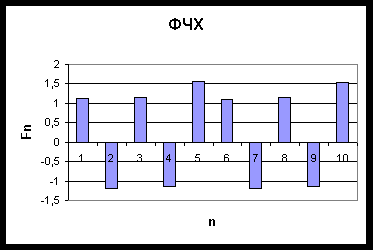
Используя полученные данные, строим графики АЧХ и ФЧХ
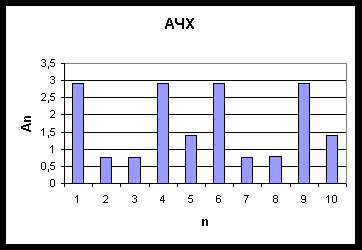ВЫВОДЫ: Особенности спектральных характеристик периодических сигналов заключаются в следующем:
1 Спектры периодических сигналов графически представляются линейчатым (дискретным) спектром.
2 Спектральные линии в периодических сигналах находятся на одинаковом расстоянии друг от друга, то есть частоты гармоник находятся в простых кратных отношениях.
Использование рядов Фурье, при расчете спектральных и временных характеристик периодических сигналов, имеет следующие преимущества:
1 Простое математическое описание
2 Инвариантность к линейчатым описаниям, т.е. если на вход действует гармоническое колебание, то и на выходе будет гармоническое колебание.
3 Как и сигнал гармонические функции являются периодическими и имеют бесконечную длительность
4 Техника генерирования гармонических функций достаточна проста.
ЛИТЕРАТУРА: С.И.Баскаков-“Радиотехнические цепи и сигналы” – М.:ВШ, 1988 И.С.Гоноровский-“ Радиотехнические цепи и сигналы”- М.:Р. и С.,1986Похожие работы
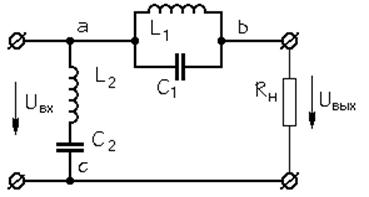
... образом мы получили разложение: . Рис 2.2 График напряжения на входе 3. Расчет фильтра для полосы частот с согласованием его на выходе с сопротивлением нагрузки Rн. Под электрическим фильтром будем понимать пассивный четырёхполюсник, пропускающий некоторую определённую полосу частот с малым затуханием и подавляющий все остальные частоты. Полоса частот, для которых затухание мало, ...
... мероприятия по обеспечению однородности выпускаемой продукции. Все эти мероприятия можно объединить в четыре группы: 1. совершенствование технологии производства; 2. автоматизация производства; 3. технологические (тренировочные) прогоны; 4. статистическое регулирование качества продукции. 2.10. Проектирование технологических процессов с использованием средств ...
... для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5 Ответ: B= Решить задачу 5, используя соотношения (8) и (9). Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел. Переменный ток долгое время не находил практического ...
... элементам управленческих систем. По отраслям и сферам применения можно выделить методы управления, применяемые в государственном управлении, бизнесе, торговле, промышленности и т.п. Для целей риск-менеджмента наиболее подходит классификация методов управления, обусловленная их содержанием. В общей совокупности методов управления рисками можно выделить семь основных групп: 1) юридические; 2) ...
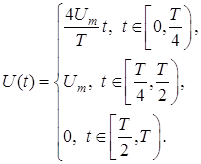
0 комментариев