Навигация
3.2 Уравнения движения
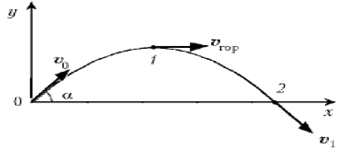
На прыгуна в полете действуют две основные силы: аэродинамическая сила и сила тяжести. Разложим аэродинамическую силу на две составляющие - подъемную силу и силу лобового сопротивления (см. рис.3) - и запишем второй закон Ньютона для центра масс системы лыжник-лыжи:
![]() , (1)
, (1)
где ![]() - сила тяжести;
- сила тяжести;
![]() - масса системы прыгун-лыжи;
- масса системы прыгун-лыжи;
![]() - ускорение центра масс системы;
- ускорение центра масс системы;
![]() - ускорение свободного падения;
- ускорение свободного падения;
![]() - подъемная сила;
- подъемная сила;
В подобных случаях под набегающим потоком воздуха понимается скорость воздуха относительно системы лыжник-лыжи. При старых техниках прыжка (см. рис. 3), когда корпус лыжника находился на относительно большом расстоянии от лыж, необходимо было рассматривать отдельно угол атаки корпуса, ног, рук и лыж [1], но при современных техниках и особенно при так называемом V-стиле, когда прыгун раздвигает лыжи и ложится между ними, становясь как бы треугольным крылом, можно приближенно считать, что лыжник и лыжи находятся в одной плоскости и рассматривать один угол атаки - угол атаки всей системы в целом.
Вернемся к началу этой главы. Для силы лобового сопротивления (2) и подъемной силы (3) существуют и другие выражения [6,7]:
![]() , (9)
, (9)
![]() , (10)
, (10)
где ![]() - плотность воздуха,
- плотность воздуха, ![]() - коэффициент силы лобового сопротивления,
- коэффициент силы лобового сопротивления,
![]() - коэффициент подъемной силы,
- коэффициент подъемной силы, ![]() - площадь миделя (площадь сечения системы прыгун-лыжи в плоскости, перпендикулярной набегающему потоку воздуха). Если считать, что лыжник и лыжи находятся в одной плоскости, то площадь миделя при заданном угле атаки
- площадь миделя (площадь сечения системы прыгун-лыжи в плоскости, перпендикулярной набегающему потоку воздуха). Если считать, что лыжник и лыжи находятся в одной плоскости, то площадь миделя при заданном угле атаки ![]() определяется следующим образом:
определяется следующим образом:![]() , где
, где ![]() - площадь миделя при угле атаки 900. Угол атаки складывается из угла
- площадь миделя при угле атаки 900. Угол атаки складывается из угла ![]() между горизонталью и скоростью и угла
между горизонталью и скоростью и угла ![]() между горизонталью и лыжами (рис. 4).
между горизонталью и лыжами (рис. 4).
Система дифференциальных уравнений (7) с аэродинамическими коэффициентами, вычисляемыми в каждый момент времени по формулам (14), (15), образует замкнутую систему уравнений. Если к ней добавить начальные условия (8), данная задача будет являться задачей Коши.
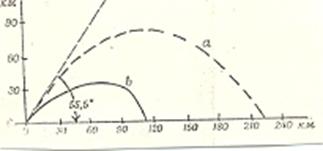
В заключение приводится сравнение реальных аэродинамических коэффициентов прыгунов 60-х и нашей оценки. Криаая А на рис. 6 изображает полученную нами зависимость между коэффициентом подъемной силы и коэффициентом лобового сопротивления, а кривая В - аналогичную зависимость, полученную из экспериментальных зависимостей аэродинамических коэффициентов от угла атаки [1]. Видно, что вид зависимости коэффициентов друг от друга слабо отличается, и коэффициент подъемной силы в нашей работе выше, чем в
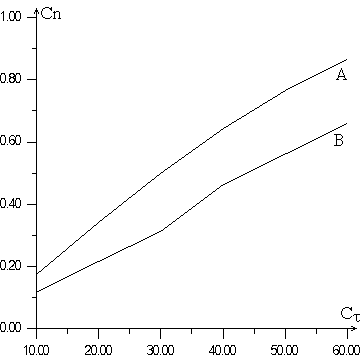
Рис. 6. Зависимость коэффициента подъемной силы от коэффициента сопротивления с углом атаки в качестве параметра (кривая А - наша оценка, кривая В - эксперименты в аэродинамической трубе с моделями прыгунов, использующих старую технику прыжка).
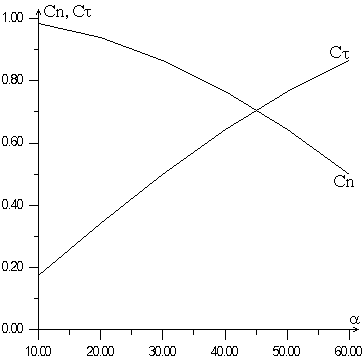
Рис. 7. Зависимость коэффициентов силы лобового сопротивления и подъемной силы от угла атаки.
экспериментах тридцатилетней давности. Это хорошо согласуется с тем фактом, что за прошедшие годы прыгуны научились развивать большую подъемную силу. Также если сравнить полученные нами графики зависимости аэродинамических коэффициентов от угла атаки (рис. 7) с аналогичными графиками в [1] на страницах 10-11, 13-14 и 15-16, видно, что вид зависимости сохранился.
![]() - сила лобового сопротивления.
- сила лобового сопротивления.
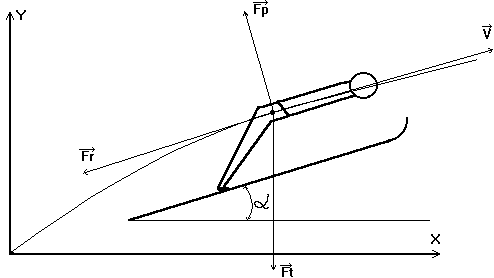
Рис. 3. Система координат и основные силы, действующие на прыгуна в полете.
Сила лобового сопротивления направлена по касательной к траектории противоположно скорости и пропорциональна квадрату модуля скорости: ![]() , (2)
, (2)
а подъемная сила направлена по нормали к траектории и по модулю равна: ![]() , (3)
, (3)
где коэффициент 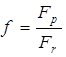 [6]. Коэффициент
[6]. Коэффициент ![]() определяется предельной скоростью системы лыжник-лыжи
определяется предельной скоростью системы лыжник-лыжи ![]() :
:
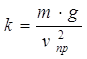 . (4)
. (4)
Предельная скорость - это скорость установившегося свободного падения тела в воздухе.
Спроецировав (1) на оси координат, путем несложных преобразований приходим к дифференциальным уравнениям движения:
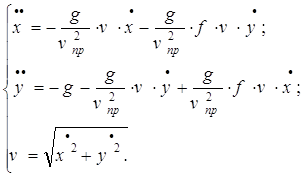 (5)
(5)
Понизим порядок системы:
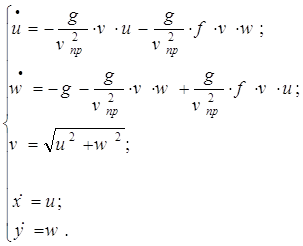 (6)
(6)
Следует также помнить, что воздушная среда находится в движении, в воздухе вокруг трамплинной горы задано векторное поле скоростей ветра. То есть все предыдущие уравнения записаны для относительных скоростей и их следует переписать для абсолютных скоростей.
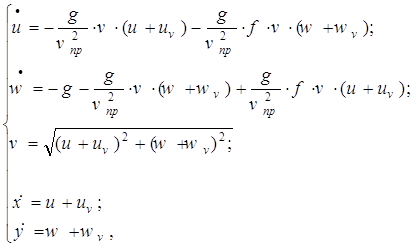 (7)
(7)
где ![]() - горизонтальная, а
- горизонтальная, а ![]() - вертикальная составляющая скорости ветра.
- вертикальная составляющая скорости ветра.
Начальные условия:
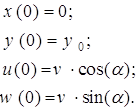 (8)
(8)
Очевидно, что в общем случае задача если и решается аналитически, то очень сложно, поэтому целесообразнее решать ее численно. Критерием окончания расчета будет служить выполнение одного из следующих условий:
пересечение траектории со склоном горы;
вылет прыгуна за пределы участка приземления:![]() .
.
Рассмотрим коэффициенты ![]() и
и![]() . В простейшей модели можно положить их постоянными, как сделано, например, в работе [4]. Однако в действительности эти коэффициенты зависят от ориентации лыжника в воздухе и от его позы. Но у нас есть достаточно оснований считать позу лрыгуна постоянной в полете, такое допущение сделано не только в этой работе, но и в работах [2 - 4]. Ориентацию же лыжника в пространстве определяет угол атаки системы прыгун-лыжи, то есть угол между плоскостью системы и скоростью набегающего потока воздуха. Здесь и далее в
. В простейшей модели можно положить их постоянными, как сделано, например, в работе [4]. Однако в действительности эти коэффициенты зависят от ориентации лыжника в воздухе и от его позы. Но у нас есть достаточно оснований считать позу лрыгуна постоянной в полете, такое допущение сделано не только в этой работе, но и в работах [2 - 4]. Ориентацию же лыжника в пространстве определяет угол атаки системы прыгун-лыжи, то есть угол между плоскостью системы и скоростью набегающего потока воздуха. Здесь и далее в
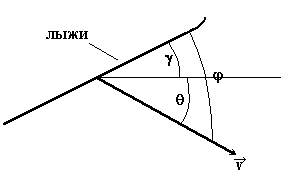
Рис. 4. Определение угла атаки системы лыжник-лыжи
(![]() - угол между лыжами и горизонталью,
- угол между лыжами и горизонталью, ![]() - угол между скоростью и горизонталью,
- угол между скоростью и горизонталью, ![]() - угол атаки).
- угол атаки).
Как видно из кинограмм прыжков, приводимых, например, в [1], и из наблюдений за прыгунами, угол между лыжами и горизонталью в полете практически не меняется, меняется лишь угол между скоростью и горизонталью. Тогда, учитывая выражения (2) и (9), можно записать:
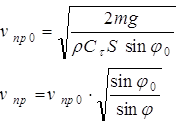 . (11)
. (11)
Из рис. 4 видно, что
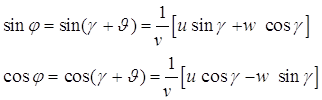 . (12)
. (12)
Аэродинамические коэффициенты ![]() и
и ![]() можно найти из опытов в аэродинамической трубе. Однако в настоящее время мы не располагаем этими данными для современных техник прыжка, поэтому в данной работе используется лишь оценка аэродинамических коэффициентов. Рассмотрим лыжника и окрыжающий его воздух. Если рассмотреть воздух, как идеальный газ, состоящий из круглых упругих частичек, то согласно теории удара аэродинамическая сила будет направлена по нормали к поверхности лыж (см. рис. 5).
можно найти из опытов в аэродинамической трубе. Однако в настоящее время мы не располагаем этими данными для современных техник прыжка, поэтому в данной работе используется лишь оценка аэродинамических коэффициентов. Рассмотрим лыжника и окрыжающий его воздух. Если рассмотреть воздух, как идеальный газ, состоящий из круглых упругих частичек, то согласно теории удара аэродинамическая сила будет направлена по нормали к поверхности лыж (см. рис. 5).
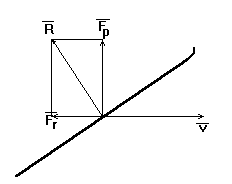
Рис. 5. Подъемная сила и сила лобового сопротивления в потоке идеального газа
(![]() - полная аэродинамическая сила, составляющими которой являются сила лобового сопротивления и подъемная сила).
- полная аэродинамическая сила, составляющими которой являются сила лобового сопротивления и подъемная сила).
Угол между скоростью и лыжами - это угол атаки ![]() . То есть коэффициент
. То есть коэффициент
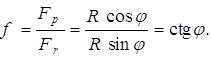 (13)
(13)
Окончательно имеем следующие выражения для ![]() и
и ![]() :
:
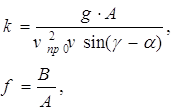 (14)
(14)
где
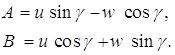 (15)
(15)
В формуле (14) ![]() - это угол отрыва, то есть угол, под которым траектория наклонена к горизонтали в начальный момент времени. Минус поставлен потому, что
- это угол отрыва, то есть угол, под которым траектория наклонена к горизонтали в начальный момент времени. Минус поставлен потому, что ![]() . Под
. Под ![]() понимается предельная скорость системы лыжник-лыжи в момент отрыва (в начальный момент времени).
понимается предельная скорость системы лыжник-лыжи в момент отрыва (в начальный момент времени).
Похожие работы
... . Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений. Целью данной курсовой работы является моделирование движения снаряда. модель параметр движение снаряд Постановка задачи Снаряд пущен с Земли с начальной скоростью v0 под углом к ее поверхности; требуется найти траекторию его движения (y), расстояние S между ...


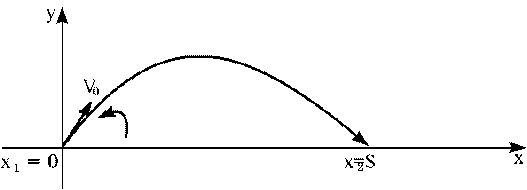
0 комментариев