Решить численно задачу Дирихле для уравнения Лапласа :
![]()
(x,y)D; u|Г=xy2=f(x,y) ;
область D ограничена линиями: x=2 , x=4 , y=x , y=x+4 ;
(x0, y0 ) = (3, 5) .
Следует решить задачу сначала с шагом по x и по y : h=0.2, потом с шагом h=0.1 . Точность решения СЛАУ =0.01 .
2.ОПИСАНИЕ МЕТОДА РЕШЕНИЯ ПОСТАВЛЕННОЙ ЗАДАЧИПоставленная задача решается численно с помощью программы, реализующей метод сеток , разработанный для численного решения задачи Дирихле для уравнений эллептического типа.
Программа написана на языке C++ , в среде Borland C++ версии 3.1. Ниже описан алгоритм работы этой программы.
1. На первом шаге область D дискретизируется. Она заменяется на область Dh путем разбиения области D параллельными прямыми по следующему правилу: yi=y0 ih, xj=x0 ih , i,j=0,1,2…. PР. Разбиение производится до тех пор, пока текущая прямая не будет лежать целиком вне области D. Получается множество точек (xi,yj).
2. За область Dh принимают те точки множества (xi,yj) , которые попали внутрь области D, а также дополняют это множество граничными точками.
3.Во всех точках области Dh вычисляются значения функции f(xi,yj) .
4. За область Dh* принимаются все внутренние точки области Dh, т.е. удовлетворяющие требованию:
(xi,yj) Dh* , если (xi+1,yj) Dh , (xi-1,yj) Dh , (xi,yj+1) Dh , (xi,yj-1) Dh .
5. Во всех точках области Dh* вычисляется функция F(N)*[i,j] ( индекс N обозначает номер итерации, на которой производится вычисление):
F(N)*[i,j]=(f(xi+1,yj) + f(xi-1,yj) + f(xi,yj+1)f(xi,yj-1))/4
6. Теперь если max | F(N+1)*[i,j] - F(N)*[i,j]|< ,взятый по всем точкам области Dh* ,то задача решена;
если нет , то выполнять шаг 5 ( пересчитывать функцию F(N)*[i,j] через значения F(N-1)*[i,j]) до тех пор, пока не выполнится указанное условие.
3.ТЕКСТ ПРОГРАММЫ#include <stdio.h>
#include <fstream.h>
#include <conio.h>
#include <iostream.h>
#include <math.h>
int i,j,k; // Variables
float h,x,y,tmp,E1;
struct point {
float xx;
float yy;
int BelongsToDh_;
int BelongsToDh;
float F;
float F_;
} p0,arrayP[13][33];
float arrayX[13];
float arrayY[33];
float diff[500];
void CreateNet(void); // Procedure Prototypes
int IsLineFit(float Param);
void CrMtrD(void);
void RegArrayX();
void RegArrayY();
void CreateDh_();
int IsFit(point Par);
void FillF();
void CreateDh();
int IsInner(int i,int j);
void FillF_();
void CountDif();
void MakeFile();
void main(void) //MAIN
{
clrscr();
p0.xx = 3;
p0.yy = 5;
h = 0.2;
p0.BelongsToDh_=1;
p0.BelongsToDh=1;
CreateNet();
RegArrayX();
RegArrayY();
CrMtrD();
CreateDh_();
FillF();
CreateDh();
FillF_();
CountDif();
while (E1>=0.005) {
for(i=0;i<13;i++)
for(j=0;j<33;j++) arrayP[i][j].F=arrayP[i][j].F_;
FillF_();
CountDif();
}
cout<<(0-arrayP[7][17].F_);
MakeFile();
getchar();
} //MAIN END
int IsLineFit(float par,char Axis) // does the line belong to the defined area
{
switch(Axis) {
case 'y': if ((par>8.0) || (par<2.0)) return 1;
else return 0;
case 'x': if (par<1.9) return 1;
else if (par>4.0) return 1;
else return 0;
}
}
void CreateNet(void) // Creation of Net (area D )
{
x = p0.xx;
i=0;
arrayX[i]=x;
while (!IsLineFit(x,'x'))
{
x += h;
i++;
arrayX[i] = x;
}
x = p0.xx-h;
i++;
arrayX[i]=x;
while (!IsLineFit(x,'x'))
{
x -= h;
i++;
arrayX[i] = x;
}
for (i=0;i<13;i++) { printf("%g ",arrayX[i]); }
printf("n");
y = p0.yy;
i = 0;
arrayY[i]=y;
while (!IsLineFit(y,'y'))
{
y += h;
i++;
arrayY[i] = y;
}
y = p0.yy - h;
i++;
arrayY[i]=y;
while (!IsLineFit(y,'y'))
{
y -= h;
i++;
arrayY[i] = y;
}
for(i=0;i<33;i++) { printf("%g ",arrayY[i]);}
printf("n");
} // end CreateNet
void RegArrayX() // Regulation of arrays X & Y
{
int LastUnreg = 13 ;
while (LastUnreg != 0) {
for(i=0;i<LastUnreg-1;i++) {
if (arrayX[i]>arrayX[i+1]) {double tmp=arrayX[i];
arrayX[i]=arrayX[i+1];
arrayX[i+1]=tmp;}}
LastUnreg=LastUnreg-1; }
for (i=0;i<13;i++) { printf("%g ",arrayX[i]);
} printf("n");
}
void RegArrayY()
{
int LastUnreg = 33 ;
while (LastUnreg != 0) {
for(i=0;i<LastUnreg-1;i++) {
if (arrayY[i]>arrayY[i+1]) { tmp=arrayY[i];
arrayY[i]=arrayY[i+1];
arrayY[i+1]=tmp;}}
LastUnreg=LastUnreg-1; }
for (i=0;i<33;i++) { printf("%g ",arrayY[i]); }
printf("n");} // End of Regulation
void CrMtrD(void) //Create general Matrix
{
for(i=0;i<13;i++)
for(j=0;j<33;j++) {arrayP[i][j].BelongsToDh_=0;
arrayP[i][j].BelongsToDh=0;}
for(i=0;i<13;i++)
for(j=0;j<33;j++) {
arrayP[i][j].xx=arrayX[i];
arrayP[i][j].yy=arrayY[j];
}
// printf("%g %g",arrayP[12][0].xx,arrayP[12][0].yy);
// printf("n");
}
int IsFit(point Par) //does point belong to area D?
{
if ((Par.xx<=4) && (Par.xx>=1.99) && (Par.yy>=Par.xx)
&& (Par.yy<=Par.xx+4)) return 1;
else return 0;
}
void CreateDh_(void) //Create area Dh_
{
for(i=0;i<13;i++)
for(j=0;j<33;j++)
if (IsFit(arrayP[i][j])) arrayP[i][j].BelongsToDh_=1;
cout << arrayP[1][1].BelongsToDh_<< "n";
cout << arrayP[1][1].xx << " " << arrayP[1][1].yy<<"n";
}
void FillF(void) // calc function F(x,y) at area Dh_
{
for(i=0;i<13;i++)
for(j=0;j<33;j++)
if (arrayP[i][j].BelongsToDh_==1)
arrayP[i][j].F=arrayP[i][j].xx*pow(arrayP[i][j].yy,2);
else arrayP[i][j].F=0;
}
int IsInner(int i,int j) //Is point inner?
{
if ((arrayP[i-1][j].BelongsToDh_==1) &&
(arrayP[i+1][j].BelongsToDh_==1) &&
(arrayP[i][j+1].BelongsToDh_==1) &&
(arrayP[i][j-1].BelongsToDh_==1)) return 1;
else return 0;
}
void CreateDh(void) //Create area Dh
{
for(i=0;i<13;i++)
for(j=0;j<33;j++)
if ((arrayP[i][j].BelongsToDh_==1) &&
IsInner(i,j))
arrayP[i][j].BelongsToDh=1;
}
void FillF_() //calc new appr. values of F
{
for(i=0;i<13;i++)
for(j=0;j<33;j++) {
if (arrayP[i][j].BelongsToDh==1)
arrayP[i][j].F_=(arrayP[i-1][j].F+arrayP[i+1][j].F+
arrayP[i][j-1].F+arrayP[i][j+1].F)/4;
else arrayP[i][j].F_=0; }
}
void CountDif() // find maximal difference abs(F-F_)
{
k=0;
for(i=0;i<13;i++)
for(j=0;j<33;j++)
{ if (arrayP[i][j].BelongsToDh==1) {
diff[k]=fabs(arrayP[i][j].F_-arrayP[i][j].F);
k++;}}
E1=diff[0];
for (k=1;k<500;k++) {
if (diff[k]>E1) E1=diff[k];}
}
void MakeFile()
{
ofstream f;
FILE *f1=fopen("surf.dat","w1");
fclose(f1);
f.open("surf.dat",ios::out,0);
for(i=0;i<13;i++)
for(j=0;j<33;j++) { if (arrayP[i][j].BelongsToDh==1) {
f<<arrayP[i][j].xx<<" "<<arrayP[i][j].yy<<
" "<<arrayP[i][j].F_<<"n";}}
f.close() ;
}
4.ГРАФИКИ РЕШЕНИЙ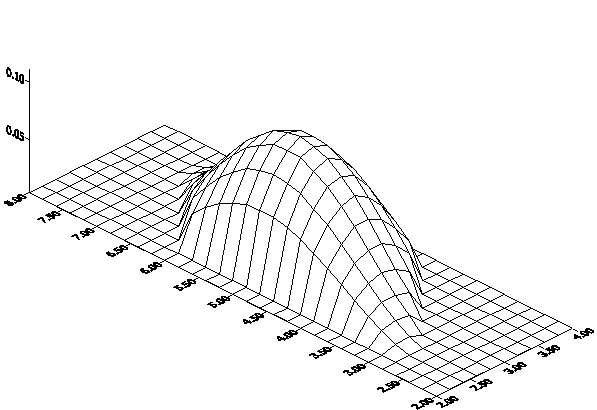
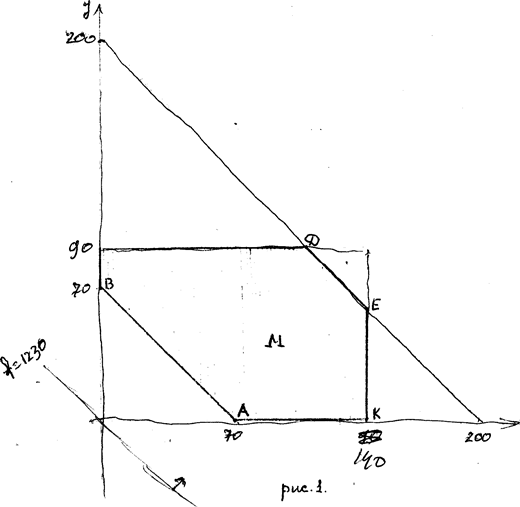
РИС.1 шаг h=0.2
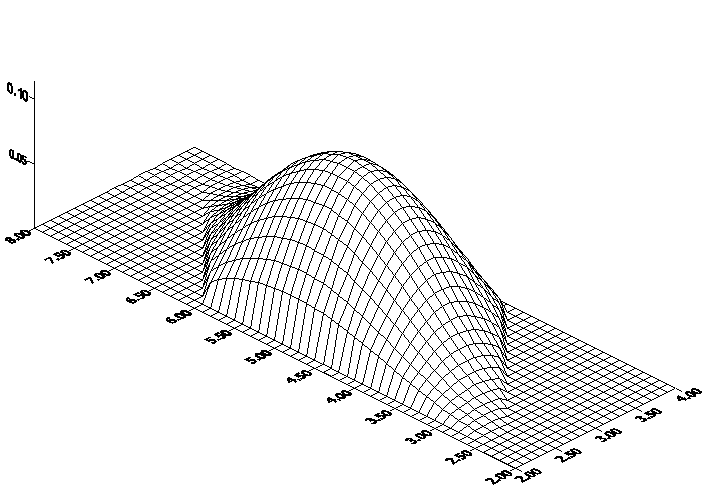
РИС.2 шаг h=0.1
5.ВЫВОДФункция f(x,y) является неотрицательной в области D. Полученное решение лежит целиком над плоскостью XOY . Для данного решения выполняется принцип максимума.
Похожие работы
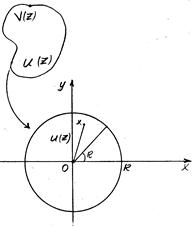
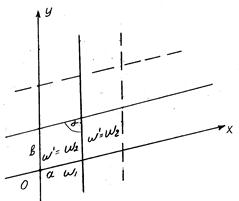
... (72) и (73) положить , то мы получим две интегральные формулы Пуассона для кругового кольца: , (82) , (83) где (74) и (75) – реальные и мнимые части компактной интегральной формулы Вилля-Шварца для кругового кольца [2], - функция Вейерштрасса, - угол наклона касательной к в точке , , - периоды, с – произвольная постоянная, (). Так как функция ) представляется быстро сходящимися ...
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... . Уравнение (2; 0,1) с оператором А, обладающим указанными свойствами, будем называть операторным уравнением первого рода, или, короче,— уравнением первого рода. 2.1. Метод подбора решения некорректно поставленных задач 2.1.1. Широко распространенным в вычислительной практике способом приближенного решения уравнения (2; 0,1) является метод подбора. Он состоит в том, что для элементов z ...
... на ak может быть не более чем ak - 1 (ведь ни одно число не даёт остаток rk), то среди них найдутся два числа, имеющих равные остатки (принцип Дирихле). Пусть это числа M + sd и M + td (0 Ј s Ј ak - 1 и 0 Ј t Ј ak - 1). Тогда их разность (M + sd) - (M + td) = (s - t)d делится на ak, что невозможно, т.к. 0 < |s - t| < ak и d = a1a2...ak - 1 взаимно просто с ak, ибо числа a1, a2, . . ., ak ...
0 комментариев