КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КУРСОВАЯ РАБОТА
на тему “вычисление определенного интеграла
методами трапеций и средних прямоугольников”
Студента 2-го курса: Полушкина О.А.
Научный руководитель: Севернева Е.В.
Минск, 1997
Содержание.
Введение, математическое обоснование и анализ задачи.
Алгоритм и его описание.
Листинг программы.
Исходные данные. Результаты расчетов и анализ.
Заключение и выводы.
Список литературы.
Введение, математическое обоснование и анализ задачи.
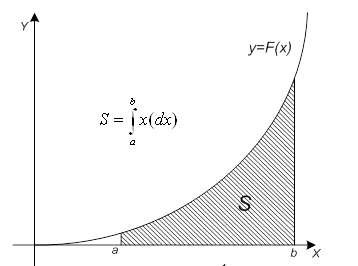
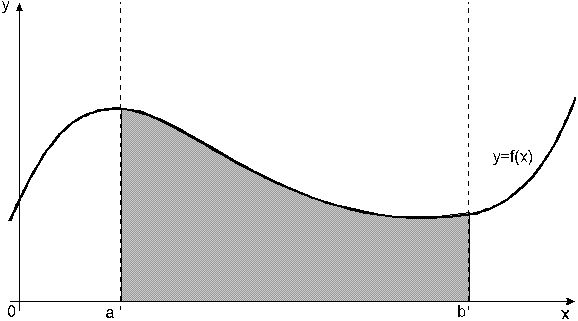
Известно, что определенный интеграл функции типа численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3).
численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3).

Рис. 1. Криволинейная трапеция.

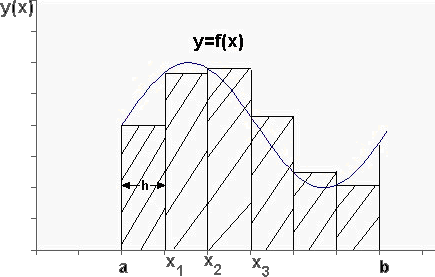
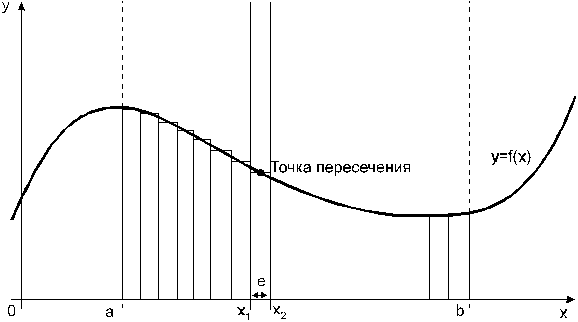
Рис. 2. Метод трапеций.

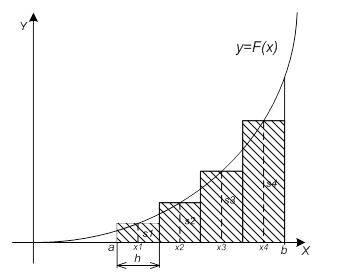
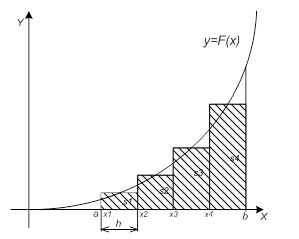
Рис. 3. Метод средних прямоугольников.
По методам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине. Соответственно получаем формулы площадей —
для метода трапеций:

,
для метода средних прямоугольников:

.
Соответственно этим формулам и составим алгоритм.
Алгоритм.

Рис. 4. Алгоритм работы программы integral.pas.
Листинг программы.
Программа написана на Tubro Pascla 6.0 для MS-DOS. Ниже приведен ее листинг:
program Integral;
uses
Crt, Dos;
var
dx,x1,x2,e,i:real;
function Fx(x:real):real;
begin
Fx:=2+x; {В этом месте запишите функцию, для вычисления интеграла.}
end;
procedure CountViaBar;
var
xx1,xx2:real;
c:longint;
begin
writeln('------------------------------------------------');
writeln('-->Метод средних прямоугольников.');
writeln('Всего итераций:',round(abs(x2-x1)/e));
i:=0;
for c:=1 to round(abs(x2-x1)/e) do begin
write('Итерация ',c,chr(13));
xx1:=Fx(x1+c*e);
xx2:=Fx(x1+c*e+e);
i:=i+abs(xx1+xx2)/2*e;
end;
writeln('------------------------------------------------');
writeln('Интеграл=',i);
end;
procedure CountViaTrap;
var
xx1,xx2,xx3:real;
c:longint;
begin
writeln('------------------------------------------------');
writeln('-->Метод трапеций.');
writeln('Всего итераций:',round(abs(x2-x1)/e));
i:=0;
for c:=1 to round(abs(x2-x1)/e) do begin
write('Итерация ',c,chr(13));
xx1:=Fx(x1+c*e);
xx2:=Fx(x1+c*e+e);
if xx2>xx1 then xx3:=xx1 else xx3:=xx2;
i:=i+abs(xx2-xx1)*e+abs(xx3)*e;
end;
writeln('------------------------------------------------');
writeln('Интеграл=',i);
end;
begin
writeln('------------------------------------------------');
writeln('-=Программа вычисления определенного интеграла=-');
writeln('Введите исходные значения:');
write('Начальное значение x (x1)=');Readln(x1);
write('Конечное значение x (x2)=');Readln(x2);
write('Точность вычисления (e)=');Readln(e);
CountViaBar;
CountViaTrap;
writeln('------------------------------------------------');
writeln('Спасибо за использование программы ;^)');
end.
Исходные данные. Результаты расчетов и анализ.
Ниже приведен результат работы написанной и откомпилированной программы:
------------------------------------------------
-=Программа вычисления определенного интеграла=-
Введите исходные значения:
Начальное значение x (x1)=0
Конечное значение x (x2)=10
Точность вычисления (e)=0.01
------------------------------------------------
-->Метод средних прямоугольников.
Всего итераций:1000
------------------------------------------------
Интеграл= 7.0100000000E+01
------------------------------------------------
-->Метод трапеций.
Всего итераций:1000
------------------------------------------------
Интеграл= 7.0150000001E+01
------------------------------------------------
Спасибо за использование программы ;^)
Расчет проверялся для функции , а определенный интеграл брался от 0 до 10, точность 0,01.
В результате расчетов получаем:
1. Интеграл  .
.
2. Методом трапеций  .
.
3. Методом средних прямоугольников .
.
Также был произведен расчет с точностью 0,1:
1. Интеграл  .
.
2. Методом трапеций .
.
3. Методом средних прямоугольников  .
.
Заключение и выводы.
Таким образом очевидно, что при вычислении определенных интегралов методами трапеций и средних прямоугольников не дает нам точного значения, а только приближенное.
Чем ниже задается численное значение точности вычислений (основание трапеции или прямоугольника, в зависимости от метода), тем точнее результат получаемый машиной. При этом, число итераций составляет обратно пропорциональное от численного значения точности. Следовательно для большей точности необходимо большее число итераций, что обуславливает возрастание затрат времени вычисления интеграла на компьютере обратно пропорционально точности вычисления.
Использование для вычисления одновременно двух методов (трапеций и средних прямоугольников) позволило исследовать зависимость точности вычислений при применении обоих методов.
Следовательно при понижении численного значения точности вычислений результаты расчетов по обеим методам стремятся друг к другу и оба к точному результату.
Список литературы.
Вольвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для ПЭВМ ЕС. Минск.: 1989 г.
Зуев Е.А. Язык программирования Turbo Pascal. М.1992 г.
Скляров В.А. Знакомьтесь: Паскаль. М. 1988 г.
Похожие работы
... n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов Задание на лабораторную работу 1) Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций: 1. f(x)=x f(x)=x2 f(x)= x3 f(x)= x4 на отрезке [0, 1] с шагом , , 2. f(x)= f(x)= f(x)= ...
... процедура TABL ) и интеграл. 4. Заключение и выводы. Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное. Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же ...
... for i: = n-1 to n do; c[i]: = 1 - c[n+1-i]; end; {заполнение y-ков в массиве у[5]} procedure form(var x:aa; var y:aa); var i:integer; Begin for i:=1 to n do y[i]:=sin(x[i]); {функция} end; {процедура для расчета интеграла по квадратурной формуле Чебышева} procedure cheb(var y:aa;var ich:real); var i:integer; Begin ich: = 0; for i: = 1 to n do ich: = ich+y[i]*h; end; {процедура вывода таблицы} ...
... разработчиками. На сегодняшний день существует широкий спектр программ от простейших, контролирующих до сложных мультимедийных продуктов. 2. Опытно-экспериментальная работа по формированию познавательной потребности у учащихся средствами информационных технологий 2.1 Особенности изучения темы "Интеграл" в школьном курсе математики Выбор темы "Интеграл" неслучаен. Тема "Интеграл" изучается ...

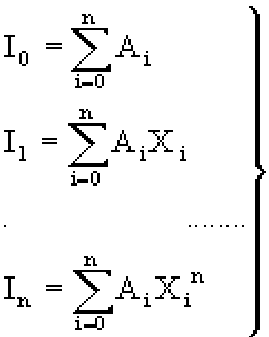



0 комментариев