Навигация
5. Прямое включение.
Обозначим входы элементов AnAND-m как . При этом:
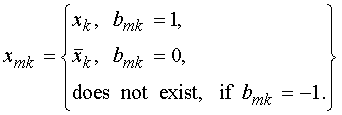(1)
Пусть все элементы AnAND-m соединены со всеми элементами AnNOT-k, т.е.
. (2)
При этом
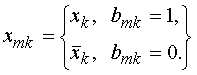(3)
Тогда из (2.5) следует, что
. 
(4)
Из (2.7) следует, что
. 
(5)
При прямом включении схемы АД выводы х являются входами, а выводы у являются выходами схемы АД. Это означает, что выводы у нагружены на очень большое сопротивление и, практически,
. (6)
Все входные потенциалы х принимают булевские значения. Пусть, кроме того, выполняется условие (2) и существует такая S-строка в матрице В, что
. 
(7)
Это означает, что булевский вектор х совпадает с S-строкой матрицы В v см. (3).
Покажем, что в этом случае все потенциалы у также принимают булевские значения.
Из (4) следует, что
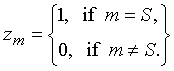(8)
Из (5) и (7) следует, что
T
, если точка 
(с потенциалом
) присоединена к одному из входов элемента AnOR-j,
T
, если точка (с потенциалом) не присоединена ни к одному из входов элемента AnOR-j.
Таким образом, все потенциалы v принимают булевские значения. Из (6) следует, что и все потенциалы у также принимают булевские значения, что и требовалось показать.
6. Обратное включение.
При обратном включении схемы АД выводы у являются входами, а выводы х являются выходами схемы АД. Все входные потенциалы у принимают булевские значения. Пусть, кроме того, существует такая S-строка в матрице G, что
. 
(1)
Это означает, что булевский вектор у совпадает с S-строкой матрицы G. Пусть еще
(2)
и, следовательно,
(3)
Существование и количество решений уравнения (4.1) относительно z определяется рангом расширенной матрицы
. Но, по условию, булевский вектор у совпадает с S-строкой матрицы G, т.е. совпадает с одним из столбцов матрицы
. Следовательно, ранг матрицы 
равен рангу матрицы. Таким образом, существование и количество решений уравнения (4.1) определяется рангом матрицы G. Точнее,
T если ранг матрицы G равен M (числу неизвестных), то (4.1) имеет единственное решение;
T если ранг матрицы G меньше M, то (4.1) имеет несколько решений;
T ранг матрицы G не может быть больше M, т.к. матрица имеет ровно столбцов.
Таким образом, решение уравнения (4.1) будет единственным, если ранг матрицы равен M или ранг G матрицы равен M. Это верно, если выполняется следующее условие, которое в дальнейшем для краткости будем называть как
Первое ранговое условие:
T в матрице все M столбцов линейно независимы,
T в матрице есть не менее M линейно независимых строк.
Если выполняется первое ранговое условие, решение уравнения (4.1) единственно, выполняется условие (1) и для строки S не существует линейно зависимых строк, то это решение имеет вид
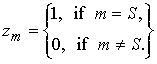(4)
Отсюда и из (5.4) следует, что
,
т.е. все потенциалы х принимают булевские значения, что и требовалось показать. Итак, для этого должно выполнятся
Второе ранговое условие:
T в матрице все M столбцов линейно независимы,
T в матрице все строки линейно независимы.
7. Таблица истинности для схемы АД
Из вышесказанного следует, что достаточное условие существования булевского решения для обратного включения заключается в следующем:
1. матрица G удовлетворяет ранговому условию;
2. вектор у совпадает с одной из строк матрицы G;
3. все элементы AnAND соединены со всеми элементами AnNOT (математически это означает, что матрица B является бинарной);
4. любое в матрице В должно принимать оба значения v 0 и 1 (в любом столбце матрицы В должен присутствовать и 0, и 1).
Схему АД будем описываеть таблицей, которая имеет вид
, где матрицы B и G удовлетворяют вышеперечисленным условиям.
Будем называть схему АД булевской, если она удовлетворяет условиям 1) и 3), а вектор у, совпадающий с одной из строк матрицы G, будем называть правильным вектором. Булевская схема АД, на которую подан правильный вектор y, имеет булевское решение.
Булевская схема АД описывается таблицей истинности, которая имеет вид
. При булевском решении
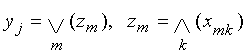
или
.
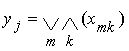Последнее выражение есть дизъюнктивная нормальная форма - ДНФ. Таким образом, схема АД, удовлетворяющая указанным условиям, удовлетворяет, кроме того, системе уравнений
,
где каждое уравнение является ДНФ. Если задается вектор х, то вычисляется вектор у, т.е. функция, соответствующая системе ДНФ. Если же вектор у задается, а вектор х вычисляется, то схема АД вычисляет функцию, обратную системе ДНФ v обратную ДНФ.
Отметим явную аналогию между схемой АД и преобразователем, реализующим ДНФ. При замене в схеме АД элементов AnAND, AnOR, AnNOT элементами AND, OR, NOT и исключении ТД онапревращается в указанный преобразователь. Отличие заключается в том, что преобразователь вычисляет ДНФ, а схема АД вычисляет как ДНФ, так и обратную ДНФ.
Похожие работы
... или кислот; так получают, например, золь гидроксида железа(III), имеющий следующее строение: {[Fe(OH)3]m n FeO+ · (n–x)Cl–}x+ x Cl– 4.2.2 Агрегативная устойчивость лиофобных коллоидов. Строение коллоидной мицеллы Лиофобные коллоиды обладают очень высокой поверхностной энергией и являются поэтому термодинамически неустойчивыми; это делает возможным самопроизвольный процесс уменьшения ...
... поколений. Естественно, особенно они заметны, если популяция находится в изоляции, т.е. отсутствует миграция генов извне. Известны сообщества такого рода в человеческом обществе. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
... показывают: Таким образом, . Совершенно аналогично: , , . В равновесных состояниях частоты гамет являются произведениями частот соответствующих генов. Верно и обратное утверждение. Часть 2 Математические модели нейронных систем Изучение нейронных систем -одно из самых романтических направлений научных исследований, поскольку нейронные системы присущи как человеку, так и животным. Самая ...
... более дорогостоящими, нежели обычные рентгеновские системы, однако по мере развития компьютерной техники и систем визуализации находят все более широкое применение. Цифровая рентгенодиагностика обеспечивается компьютерной технологией.Дисплей Блок долговременной памяти Устройство документирования Компьютер + память изображенияИнтерфейс данныхПриемник изображения Пациент Рентгеновский аппарат ...
0 комментариев