В. В. Орлёнок, доктор геолого-минералогических наук
Нахождение аномалий силы тяжести, создаваемых телами известной формы, составляет прямую задачу гравиметрии. В основе аналитического способа решения прямой задачи лежит известный закон всемирного тяготения Ньютона, согласно которому притяжение единичной массы (весом 1 г) элементарной массой равно
. (V.4)
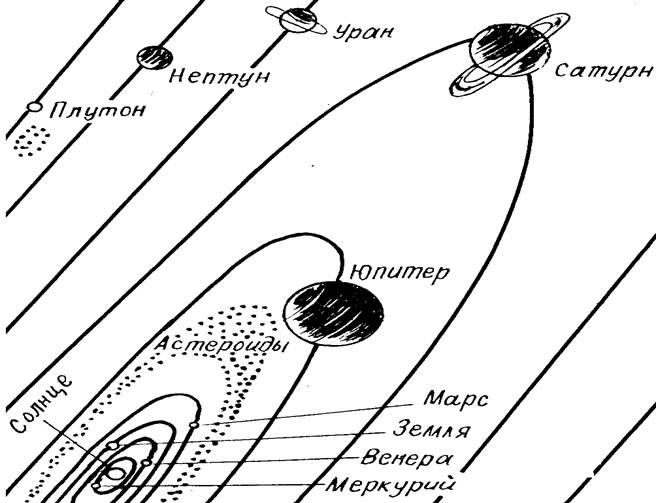
Положим, что точка с массой dm находится на расстоянии r от пункта наблюдения и на глубине h от поверхности Земли (рис. 26). Потенциал точки будет
, (V.5)
где 
, т.е.
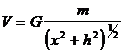. (V.6)
Из определения силы тяжести (см. гл. 4, §3) ее вертикальная и горизонтальная составляющие определяются как первая и вторая производные по h и x:
; (V.7)
. (V.8)
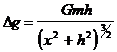; (V.9)
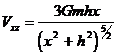. (V.10)
Максимальное и минимальное значение Dg принимает при x = 0 и x = ±¥:
. (V.11)
. (V.12)
Графики функций Dg и Vxz приведены на рис. 26.
Притяжение шара. Многие геологические тела в земной коре могут быть аппроксимированы шаром (купола, дайки, подводные холмы и т.д.). Предположим, что шар массой М залегает на глубине h и на расстоянии r от точки наблюдения, расположенной на поверхности земли (рис. 27). Будем считать шар однородным по плотности. Поместим его под центром системы координат xoz (y = 0). Притяжение шара эквивалентно притяжению точки, помещенной в центр шара. Поэтому можно воспользоваться формулой, полученной для элементарной массы (V.9):
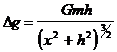. (V.13)
Аналогично имеем для второй производной потенциала силы тяжести Vxz:
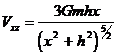. (V.14)
В плане гравитирующим массам, имеющим форму, близкую к шару, соответствуют изометрические аномалии, максимум которых располагается над центром тяжести шара (рис. 27).
Таким образом, над центром шара вертикальная составляющая силы тяжести Dg имеет максимум, горизонтальная составляющая Vxz – минимум. С удалением от шара кривые Dg и Vxz асимметрически приближаются к оси x (рис.
Похожие работы
... породы. При этом толщина коры становится меньше и в среднем составляет 10-15 км. Особенно тонкой кора становится в глубоководных впадинах (4-5 км). Аномальное гравитационное поле Земли отражает суммарное действие гравитирующих масс, расположенных на различных глубинах в земной коре и верхней мантии. Несмотря на сложную ...
... , полученное выражение (V.16) проинтегрируем в пределах от h1 до h2: (V.17) Для стержня бесконечной длины (h2 ® ¥): . (V.18) Дифференцируя (V.18) по x, найдем Vxz: . (V.19) При x = 0 . (V.20) Графики Dg и Vzx показаны на рис. 28. Сравнивая их с аналогичными графиками для шара, нетрудно убедиться в сходстве полей Dg и Vzx для шара и вертикального стержня. В плане поле стержня также
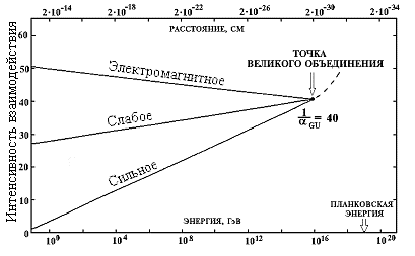
... представляют собой проявление одного и того же фундаментального принципа. Эйнштейн опередил свое время. В то время, когда он жил, еще не было известно сильное и слабое взаимодействие, поэтому он так и не смог выстроить Единую Теорию Поля. Больше того, его поиски в то время были мало понятны большинству физиков - почти все из них были озабочены разработкой новой дисциплины - квантовой механикой. ...
... в духе «Системы природы» Гольбаха или «Диалектики природы» Энгельса, а в контексте философской картины мира, которая включает не только онтологический, но одновременно и гносеологический анализ. Эта тенденция к синтезу онтологического и гносеологического подходов в рамках исследования научной картины мира, насколько мы можем судить, характерна для большинства современных работ как отечественных, ...
0 комментариев