Асп. Плиева Л.Ю.
Кафедра математического анализа.
Северо-Осетинский государственный университет
Статья посвящена одному квадратурному процессу, построенному Д.Г. Саникидзе в 1965 г. для вычисления некоторых несобственных интегралов. Вычислены коэффициенты, узлы для конкретных значений 
.
В приближенных вычислениях особое место занимают квадратурные формулы с наивысшей степенью точности. Их преимущество перед другими обычными квадратурными формулами заключается в том, что в них применяется минимальное количество узлов, коэффициентов и результаты получаются с наименьшей погрешностью. Квадратурные формулы указанного типа были построены еще в XIX в. Гауссом. Поэтому такие квадратурные формулы получили название квадратурных формул Гаусса. В дальнейшем в развитие этой теории значительный вклад внесли А.Крылов и В.Крылов [1].
Здесь же мы рассмотрим квадратурную формулу, которая была построена в 1965 г. грузинским математиком Саникидзе Д.Г. [2]. Он построил ее для вычисления несобственных интегралов вида:
, (1)
где 
– весовая функция и 
, а 
– дифференцируемая до определенного порядка функция.
Итак, квадратурная формула для (1) имеет вид:
,
где 
,
, 
,
,
.
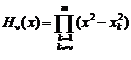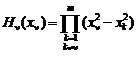Здесь 
являются узлами квадратурной формулы, 
, 
– коэффициентами, а 
– остаточным членом.
В статье Д.Г.Саникидзе [2] приведена таблица узлов и коэффициентов для случая 
, которые не позволяют вычислить интеграл с более высокой степенью точности из-за отсутствия дальнейших значений узлов и коэффициентов.
Наша задача заключалась в том, чтобы построить указанную квадратурную формулу для конкретных значений .
В [2] вычисляют из следующей системы нелинейных уравнений:
(
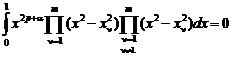). (2)
Используя свойства ортогональности многочленов, можно (2) заменить следующей эквивалентной системой:
. (3)
Отсюда для любого 
мы будем получать формулы Вьета, т. е. наша задача свелась к решению обыкновенного алгебраического уравнения -ой степени:
(4)
где 
. Для его решения и вычисления коэффициентов была составлена программа на языке Паскаль для значений:
.
Ниже мы приводим полученные результаты для 
и 
:
, 
1,072244199477261880,
0,505492653760114758, 
0,421908758347199805,
0,888813304815261389, 
0,153346705375644365,
16,705000673599787900,
0,021010252334716897, 1,018984571918536970,
0,103866983666919520, 0,481159060055772372,
0,239874720072333520, 0,304701660614504889,
0,410803984491100701, 
0,210697676646705469,
0,593708243717703457, 
0,148242465067985048,
0,764030577337008023, 
0,100794530327821750,
0,898906161681775344, 
0,061185532509305821,
0,980260135888473404, 
0,025642390273945643,
15,297184223170844100;
0,011538570831164812, 0,992093361560775528
0,057797996308034946, 
0,475206996405231443,
0,136691350037226988, 0,309481687628868688,
0,242410221548385496, 
0,224182021687137567,
0,367149993172128210, 
0,170025942566687891,
0,501699747781751390, 
0,131105212017457282,
0,636123814574765828, 0,100675698014444633,
0,760495808704081177, 
0,075350705067579744,
0,865631994733214915, 
0,053206548788294829,
0,943770905120913118, 
0,033031548416791457,
0,989161252517134264, 
0,014001581712479520,
14,843217392368502800.
Замечание. При проверке достоверности полученных результатов на многочисленных примерах оказалось, что при 
погрешность округления значительно влияет на точность результатов. Следовательно, желательно использовать полученные результаты при 
.
1. Крылов В. И. Приближенное вычисление интегралов. М.: Физ. мат. изд., 1959.
2. Саникидзе Д. Г. О приближенном вычислении некоторых несобственных интегралов // Труды Тбилисского мат. университета, 1965. Т.1
Похожие работы
... , в котором используются некоторые значения подынтегральной функции. В качестве квадратурного выражения обычно выбирают взвешенную сумму значений подынтегральной функции. 1. Вычисление определенных интегралов Количество параметров квадратурного выражения тесно связано со степенью подынтегральной функции, если последняя может быть описана степенным полиномом ограниченной степени. В общем ...
... на главной и двух побочных диагоналях, равны нулю при та В общем случае системы линейных алгебраических уравнений с трехдиагональной матрицей имеют вид Для численного решения систем трехдиагональными матрицами применяется метод прогонки, который представляет собой вариант метода последовательного исключения неизвестных. Т.е. матрицу А можно записать Идея метода прогонки состоит в ...
... ('Введите значение погрешности: '); readln(eps); write ('Введите начальное значение количества разбиений: '); readln(n); writeln; gr (a, b); write ('Ждите, идет обработка данных '); m0:=0; writeln (lf, ' КУРСОВАЯ РАБОТА'); writeln (lf, ' ПО КУРСУ ИНФОРМАТИКА'); writeln (lf, ' «ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ'); writeln (lf, ' ОПРЕДЕЛЕННОГО ИНТЕГРАЛА» '); writeln (lf, ' Выполнил: студ
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
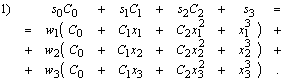
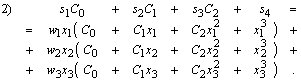
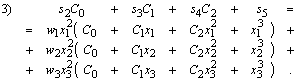
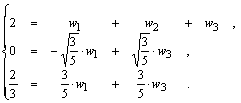
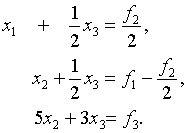
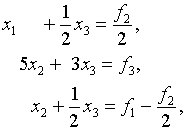
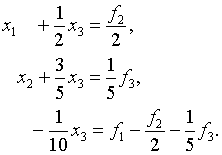
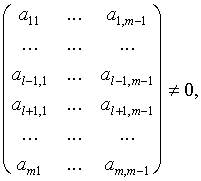
0 комментариев