Навигация
| x1 | x2 | x4 | x5 | ||
| x1 | ¥ | 1 | 01 | ¥ | |
| x4 | 00 | ¥ | ¥ | ¥ | 1 |
| x5 | 01 | 01 | 1 | ¥ | |
| x6 | 6 | ¥ | 00 | 00 | |
Продолжаем по ![]() 23
23![]() 36
36![]() 45. Дробим по переходу x5-x1:
45. Дробим по переходу x5-x1:
Таблица ![]() 23
23![]() 36
36![]() 45
45![]() 51 å =14+1=15
51 å =14+1=15
| x2 | x4 | ||
| x1 | 1 | ¥ | 1 |
| x6 | ¥ | 00 | |
Таблица ![]() 23
23![]() 36
36![]() 45
45![]() 51 å =14+6=20
51 å =14+6=20
| x1 | x2 | x4 | ||
| x1 | ¥ | 1 | 01 | |
| x5 | ¥ | 01 | ¥ | |
| x6 | 0 | ¥ | 00 | |
| 6 |
Окончательно имеем Гамильтонов контур: 2,3,6,4,5,1,2.
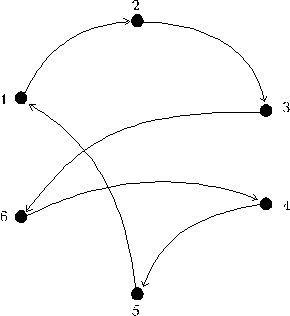
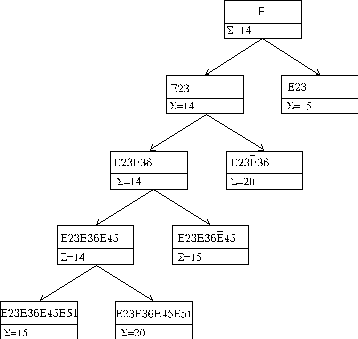
Прадерево разбиений:

Задача 10 (Задача о назначениях) Дан полный двудольный граф Knn с вершинами первой доли x1, x2,...xn.и вершинами другой доли y1, y2,...yn..Вес ребра {xi,yj} задается элементами vij матрицы весов. Используя венгерский алгоритм, найти совершенное паросочетание минимального (максимального веса). Выполнить рисунок.
Матрица весов двудольного графа K55 :
| y1 | y2 | y3 | y4 | y5 | |
| x1 | 2 | 0 | 0 | 0 | 0 |
| x2 | 0 | 7 | 9 | 8 | 6 |
| x3 | 0 | 1 | 3 | 2 | 2 |
| x4 | 0 | 8 | 7 | 6 | 4 |
| x5 | 0 | 7 | 6 | 8 | 3 |
Первый этап - получение нулей не нужен, т. к. нули уже есть во всех строк и столбцах.
Второй этап - нахождение полного паросочетания.
| y1 | y2 | y3 | y4 | y5 | |
| x1 | 2 | 0 | 0 | 0 | 0 |
| x2 | 0 | 7 | 9 | 8 | 6 |
| x3 | 0 | 1 | 3 | 2 | 2 |
| x4 | 0 | 8 | 7 | 6 | 4 |
| x5 | 0 | 7 | 6 | 8 | 3 |
Третий этап - нахождение максимального паросочетания.
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 2 | 0 | 0 | 0 | 0 | X |
| x2 | 0 | 7 | 9 | 8 | 6 | X |
| x3 | 0 | 1 | 3 | 2 | 2 | |
| x4 | 0 | 8 | 7 | 6 | 4 | |
| x5 | 0 | 7 | 6 | 8 | 3 | |
| X | X |
Четвертый этап - нахождение минимальной опоры.
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 2 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 7 | 9 | 8 | 6 | 5 |
| x3 | 0 | 1 | 3 | 2 | 2 | 1 |
| x4 | 0 | 8 | 7 | 6 | 4 | 2 |
| x5 | 0 | 7 | 6 | 8 | 3 | 3 |
| 4 |
Пятый этап - возможная перестановка некоторых нулей.
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 6 | 8 | 7 | 5 | 5 |
| x3 | 0 | 0 | 2 | 1 | 1 | 1 |
| x4 | 0 | 7 | 6 | 5 | 3 | 2 |
| x5 | 0 | 6 | 5 | 7 | 2 | 3 |
| 4 |
Решение с ненулевым значением. Переход ко второму этапу.
Полное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 6 | 8 | 7 | 5 | |
| x3 | 0 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 7 | 6 | 5 | 3 | |
| x5 | 0 | 6 | 5 | 7 | 2 | |
Максимальное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | X |
| x2 | 0 | 6 | 8 | 7 | 5 | X |
| x3 | 0 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 7 | 6 | 5 | 3 | |
| x5 | 0 | 6 | 5 | 7 | 2 | |
| X | X |
Минимальная опора:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | 6 |
| x2 | 0 | 6 | 8 | 7 | 5 | 7 |
| x3 | 0 | 0 | 2 | 1 | 1 | 1 |
| x4 | 0 | 7 | 6 | 5 | 3 | 2 |
| x5 | 0 | 6 | 5 | 7 | 2 | 3 |
| 4 | 5 |
Перестановка нулей:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | 6 |
| x2 | 0 | 6 | 8 | 7 | 5 | 7 |
| x3 | 0 | 0 | 2 | 1 | 1 | 1 |
| x4 | 0 | 7 | 6 | 5 | 3 | 2 |
| x5 | 0 | 6 | 5 | 7 | 2 | 3 |
| 4 | 5 |
Полное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | 6 |
| x2 | 0 | 6 | 8 | 7 | 5 | 7 |
| x3 | 0 | 0 | 2 | 1 | 1 | 1 |
| x4 | 0 | 7 | 6 | 5 | 3 | 2 |
| x5 | 0 | 6 | 5 | 7 | 2 | 3 |
| 4 | 5 |
Максимальное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | X |
| x2 | 0 | 6 | 8 | 7 | 5 | |
| x3 | 0 | 0 | 2 | 1 | 1 | X |
| x4 | 0 | 7 | 6 | 5 | 3 | X |
| x5 | 0 | 6 | 5 | 7 | 2 | |
| X | X | X |
Минимальная опора:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 3 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 6 | 8 | 7 | 5 | 1 |
| x3 | 0 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 7 | 6 | 5 | 3 | |
| x5 | 0 | 6 | 5 | 7 | 2 | 2 |
| 3 |
Перестановка нулей:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 4 | 6 | 5 | 3 | 1 |
| x3 | 2 | 0 | 2 | 1 | 1 | |
| x4 | 2 | 7 | 6 | 5 | 3 | |
| x5 | 0 | 4 | 3 | 5 | 0 | 2 |
| 3 |
Полное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 4 | 6 | 5 | 3 | |
| x3 | 2 | 0 | 2 | 1 | 1 | |
| x4 | 2 | 7 | 6 | 5 | 3 | |
| x5 | 0 | 4 | 3 | 5 | 0 | |
Максимальное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | X |
| x2 | 0 | 4 | 6 | 5 | 3 | X |
| x3 | 2 | 0 | 2 | 1 | 1 | X |
| x4 | 2 | 7 | 6 | 5 | 3 | |
| x5 | 0 | 4 | 3 | 5 | 0 | X |
| X | X | X | X |
Минимальная опора:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 4 | 6 | 5 | 3 | |
| x3 | 2 | 0 | 2 | 1 | 1 | |
| x4 | 2 | 7 | 6 | 5 | 3 | 1 |
| x5 | 0 | 4 | 3 | 5 | 0 | |
Перестановка нулей:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 4 | 6 | 5 | 3 | |
| x3 | 2 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 5 | 4 | 3 | 1 | 1 |
| x5 | 0 | 4 | 3 | 5 | 0 | |
Полное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 4 | 6 | 5 | 3 | |
| x3 | 2 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 5 | 4 | 3 | 1 | 1 |
| x5 | 0 | 4 | 3 | 5 | 0 | |
Максимальное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | X |
| x2 | 0 | 4 | 6 | 5 | 3 | X |
| x3 | 2 | 0 | 2 | 1 | 1 | X |
| x4 | 0 | 5 | 4 | 3 | 1 | |
| x5 | 0 | 4 | 3 | 5 | 0 | X |
| X | X | X | X |
Минимальная опора:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 5 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 4 | 6 | 5 | 3 | 3 |
| x3 | 2 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 5 | 4 | 3 | 1 | 1 |
| x5 | 0 | 4 | 3 | 5 | 0 | |
| 2 |
Перестановка нулей:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 6 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 3 | 5 | 4 | 2 | 3 |
| x3 | 3 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 4 | 3 | 2 | 0 | 1 |
| x5 | 1 | 4 | 3 | 5 | 0 | |
| 2 |
Полное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 6 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 3 | 5 | 4 | 2 | 3 |
| x3 | 3 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 4 | 3 | 2 | 0 | 1 |
| x5 | 1 | 4 | 3 | 5 | 0 | |
| 2 |
Максимальное паросочетание:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 6 | 0 | 0 | 0 | 0 | X |
| x2 | 0 | 3 | 5 | 4 | 2 | X |
| x3 | 3 | 0 | 2 | 1 | 1 | X |
| x4 | 0 | 4 | 3 | 2 | 0 | |
| x5 | 1 | 4 | 3 | 5 | 0 | X |
| X | X | X | X |
Минимальная опора:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 6 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 3 | 5 | 4 | 2 | 4 |
| x3 | 3 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 4 | 3 | 2 | 0 | 1 |
| x5 | 1 | 4 | 3 | 5 | 0 | 5 |
| 2 | 3 |
В результате имеем:
| y1 | y2 | y3 | y4 | y5 | ||
| x1 | 6 | 0 | 0 | 0 | 0 | |
| x2 | 0 | 1 | 3 | 2 | 2 | 4 |
| x3 | 3 | 0 | 2 | 1 | 1 | |
| x4 | 0 | 2 | 1 | 0 | 0 | 1 |
| x5 | 1 | 4 | 3 | 5 | 0 | 5 |
| 2 | 3 |
Исходный граф
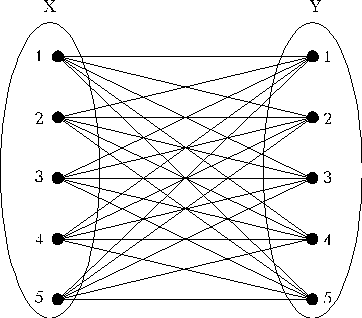
Полученный граф:
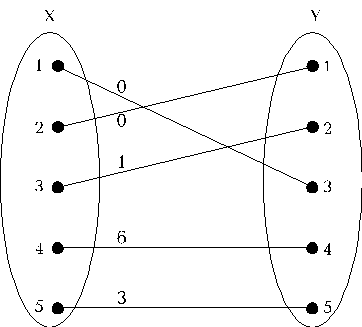
Вес найденного совершенного паросочетания = 12.
Задача 11 Решить задачу 10, используя алгоритм ветвей и границ (отождествив вершины xi и yj).
Таблица Е (исходная). Строки - xi , столбцы - yj. å =0
| 1 | 2 | 3 | 4 | 5 | ||
| 1 | 2 | 01 | 03 | 02 | 02 | |
| 2 | 06 | 7 | 9 | 8 | 6 | |
| 3 | 01 | 1 | 3 | 2 | 2 | |
| 4 | 04 | 8 | 7 | 6 | 4 | |
| 5 | 03 | 7 | 6 | 8 | 3 | |
Дробим по переходу x2 - y1:
Таблица Е21 å =0+8=8
| 2 | 3 | 4 | 5 | ||
| 1 | 00 | 02 | 01 | 00 | |
| 3 | 01 | 2 | 1 | 1 | 1 |
| 4 | 4 | 3 | 2 | 02 | 4 |
| 5 | 4 | 3 | 5 | 03 | 3 |
Таблица
Похожие работы
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... статистической информации на ЭВМ. 3. Организация решения статистических задач с помощью комплекса средств новой технологии для обработки статистической информации. Одной из главных особенностей автоматизированной обработки статистической информации является новая технология, обеспечиваю- щая более эффективную обработку на основе достижения технической, программной, ...
... чертеж – документ, содержащий изображение сборочной единицы и другие данные, необходимые для ее сборки, изготовления и контроля. К сборочным чертежам также относят гидромонтажные, пневмомонтажные и электромонтажные чертежи; чертеж общего вида – документ, определяющий конструкцию изделия, взаимодействие его составных частей и поясняющий принцип работы изделия; ...
... документооборота сдают производственные отчеты до 25 числа каждого месяца в вышестоящую организацию. Как и многие хозяйства ЗАО «Нива» утвердило основной формой бухгалтерского учета – журнально-ордерную. 3. Учет расчетов по оплате труда работников растениеводства в Закрытом Акционерном Обществе «Нива» Песчанокопского района. 3.1 Первичный учет. Процесс производства связан с затратами не ...


0 комментариев