Навигация
Стимулирующие приемы проявления прикладных функций задач
81552
знака
1
таблица
1
изображение
3.3. Стимулирующие приемы проявления прикладных функций задач.
1) Использование возможностей варьирования содержания прикладных задач. Прикладная задача имеет более конкретное содержание, чем задачи других видов. Варьируя содержанием, можно показать многообразие приложений теории или возможность приложения одной и той же теории в разных случаях. Например, дана задача на определение недоступного расстояния. В целях усиления прикладной функции полезно вспомнить, в каких сходных ситуациях используются подобные расчеты: прокладка трубопроводов, шоссейных и железных дорог, линий электропередач. На чертежах, выполненных в учебниках, недоступность точки обычно обусловлена наличием водной преграды, кустарника; можно указать и на помехи от холмов, оврагов, огородов, городских площадей и дорог с интенсивным движением.
После решения задачи об освещенности, напрашивается необходимость определить освещенность класса, квартиры.
2) Сообщение дополнительных сведений прикладного характера.
Задача: 17 всего поля засеяли пшеницей. 57 засеяли рожью. Оставшуюся часть поля оставили под другую культуру. Какую часть поля оставили пока не засеянной?
Здесь уместно рассказать об этих культурах, спросить, что о них знают дети, рассказать какое значение для человека они имеют, когда люди впервые начали выращивать.
3) Указание па прикладные возможности познавательных задач. Любая геометрическая задача представляет какую-либо степень абстрагирования от прикладной ситуации. Познавательная задача, таким образом, вторична по отношению к прикладной. После решения познавательной задачи мы предлагаем учащимся «привести пример из жизни», связанный с этой задачей. «Какую жизненную ситуацию отражает содержание? Какую производственную ситуацию отражает, описывает, моделирует задача?»
Например: «нужно разделить площадь квадрата части». Соответствующая прикладная задача: «На школьном участке имеется квадратная клумба со стороной в 5 метров. На 25 от ее площади необходимо посадить гвоздики. На остальной части посадят другие цветы. С помощью рулетки определите 25 площади, на которой необходимо посадить гвоздики.
Новые особенности поиску решения задач придает использование микрокалькуляторов. Задачи производственного характера отпугивают учащихся именно тем, что числовые данные и вычисления в них «менее удобны», чем в обычных задачах. При использовании же вычислительной техники мышление направлено на анализ ситуации, на составление модели, выражения, вычисление значения которого не представляет особых трудностей; решение отступает на второй план.
Оформление содержания и решения прикладных задач также имеет свои особенности. Оно сопровождается рисунками, чертежами, иногда выполняется не в тетрадях, а на отдельных листах, дополняется расчетами в форме таблиц, графиков, ведомостей, диаграмм. Текст задачи может быть представлен как задание от имени дирекции школы, администрации предприятия и т.д.
Таким образом, стимулирующие приемы развивающего, дидактического и прикладного характера безусловно являются неотъемлемой часть процесса стимулирования математической деятельности в процессе поиска решения задач. Все многообразие стимулирующих приемов будет бесполезно, если учитель не будет их постоянно использовать, дорабатывать, практиковать, применять, не только при решении задач но и на протяжении всех уроков.
Стимулы должны стать помощниками учителя. Воздействуя стимулами на мотивы младших школьников, учитель будет добиваться наивысших результатов в своей деятельности.
Для того, чтобы узнать как стимулы будут влиять на процесс поиска решения задач, мы провели эксперимент. В эксперименте был взят определенный тип задач, задачи с дробями.
§4. Опытно-экспериментальная работа.Для решения выдвинутой гипотезы о том, что если использовать комплект стимулирующих приемов (материальное поощрение как стимулирующий прием, моральное поощрение, схематическое построение задачи, оформление содержания наглядным материалом, решение пройденной задачи… ), то это будет способствовать более осознанному изучению программного материала младшими школьниками, повысится уровень мотивации младших школьников при решении задач, мы провели опытно – экспериментальную работу.
Базой экспериментальной работы был лицей №1 г. Комсомольска-на-Амуре. Эксперимент проводился в 3А классе, обучающийся по системе развивающего обучения Л.В. Занкова, 3-й четверти, в течении 10 уроков.
Исследование проводилось в 3 этапа.
1 этап – констатирующий эксперимент;
2 этап – обучающий эксперимент;
3 этап – контрольный эксперимент.
1. Констатирующий эксперимент.
Констатирующий эксперимент проходил с целью выявления реального уровня качества знаний по умению решать задачи с дробями, как в прямой, так и в косвенной форме без специально организованного обучения. К данному времени дети изучали тему «Дроби», в соответствии с программой.
Эксперимент проводился в виде задания, в котором было предложено решить сначала задачу с дробями в прямой форме, а затем и в косвенной форме. На констатирующий эксперимент отводилась 2 дня.
Школьникам были предложены 2 задачи с дробями (прямая №1 и косвенная форма №2), оформленные в виде индивидуальных карточек.
Балл «5» ставится за работу с краткой записью к задаче, правильным решением задачи с пояснением и за полный ответ; «4» за неправильный ответ, но краткой записью, решением с пояснением, и полный ответ; «3» за неправильный ответ, без краткой записи, либо без решения с пояснением, либо без полного ответа; «2» за неправильный ответ и выполненное хотя бы одно условие из всех.
Задача 1.
Прочитайте задач. 1)составьте к задаче краткую запись. 2)решение с пояснением. 3)полный ответ.
Фермер собрал на своем поле 864 кг моркови. 
Часть этого урожая отдал в детский сад. 
часть от оставшегося урожая отдал в школу, остальное оставил себе. Сколько килограммов моркови оставил себе фермер?
1) 864:8=108 (кг) – столько отдал в дсад.
2) 864-108=756 (кг) - столько осталось после того как он отдал в дсад
3) 756:3=252 (кг) – столько он отдал в школу.
4) 756-252=504 (кг) – оставил себе.
Ответ: 504 гк. oставил себе
Задача 2.
Прочитайте задач. 1)составьте к задаче краткую запись. 2)решение с пояснением. 3)полный ответ.
В школу поступило 125 парт. Это в 2 раза меньше, чем поступивших вместе с партами стульев. Но стульев оказалось 
бракованных. 
бракованных стульев смогли отремонтировать. Какое количество стульев не смогли отремонтировать?
1) 125*2=250 (шт) – количество стульев
2) 250:10=25 (шт) – количество бракованных стульев
3) 25:5*4=20 (шт) – смогли отремонтировать
4) 25-20=5 (шт) – не смогли отремонтировать
Ответ: 5 стульев не смогли отремонтировать.
Констатирующий эксперимент показал следующие результаты.
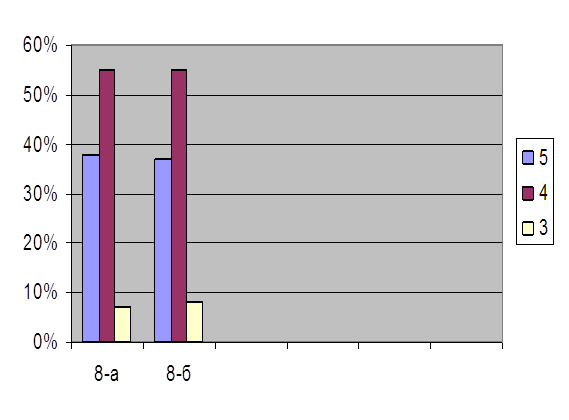
Прямая форма задачи: из 23 учеников на «5» решили 12 чел. (52%), на «4» - 3 чел. (13%), на «3» - 5 чел. (22%), «2» - 3 чел. (13%).
Косвенная форма задачи: из 23 учеников на «5» решили 10 чел. (44%), на «4» - 4 чел. (17%), на «3» - 4 чел. (17%), «2» - 5 чел. (22%).
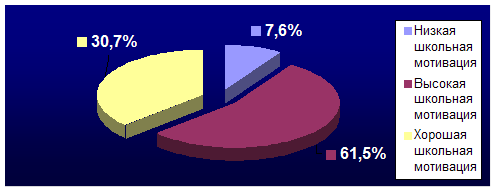
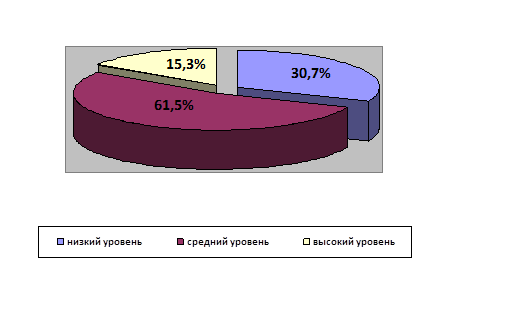
Результаты констатирующего эксперимента приведены в таблице 1 и на рис. 4 и рис. 5
(см. Приложение 3).
Исходя из результатов констатирующего эксперимента, можно сделать предварительные выводы.
Процент правильно решенных задач говорит о том, что у учащихся не до конца сформировано умение решать задачи с дробями. Больший процент у прямой формы задачи с дробями, чем у косвенной форме задачи с дробями говорит о том, что данный тип задачи по системе развивающего обучения Л.В. Занкова практически не рассматриваются. В косвенной форме процент решений на «2» превышает решения на «3» и «4», что еще раз доказывает о том, что такая форма затруднительна для учащихся и необходимо стимулировать процесс поиска решения задачи с дробями, как в косвенной форме, так и в прямой.
Похожие работы
... учителя); продолжается работа по самообучению. Наиболее глубоко и полно система учебной работы по развитию самостоятельности и творческой активности школьников реализуется при изучении факультативных курсов по математике. 2. ОБУЧЕНИЕ ЧЕРЕЗ ЗАДАЧИ Метод обучения математике через задачи базируется на следующих дидактических положениях: 1) Наилучший способ обучения учащихся, дающий им ...
... свидетельствует положительная динамика по тем параметрам, которые нами были определены. Разумеется, наше исследование не раскрывает всех сторон проблемы влияния личностно-ориентированного подхода на эффективность процесса обучения младших школьников, поэтому не является исчерпывающим. Перспективным направлением мы считаем обоснование влияния личностно-ориентированного подхода на другие качества ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
... прежнем уровне. В экспериментальном классе, котором были проведены ряд зачетных уроков, повысился уровень знаний. В ходе написания выпускной квалификационной работы по теме « Зачет как одна из форм контроля знаний учащихся по алгебре в 8 классе» были реализованы поставленные цели и задачи. Гипотеза дала положительный результат. Таким образом, разнообразие форм проверки знаний и их сочетания в ...
0 комментариев