Обучающий эксперимент

2. Обучающий эксперимент

Формирующий эксперимент проводится с целью проверки влияния небольшого набора стимулирующих приемов на процесс поиска решения задач с дробями.

Были даны 2 типа задач с дробями: прямая (задача 1) и косвенная форма (задача 2). Эксперимент проводился в течении 2 дней.

Критерии оценки остались прежними.

В ходе решения задачи были введены стимулирующие приемы для 2 типов задач, такие как:

- решение пройденной задачи.

- построение вместе с учащимися схемы к задаче.

- оформление содержания задачи наглядным материалом.

Данные стимулирующие приемы должны способствовать повышению уровня мотивации у учащихся, способствовать развитию более осознанному, правильному процессу решению задачи.

Задача 1.

Прочитайте задач. 1)составьте к задаче краткую запись. 2)решение с пояснением. 3)полный ответ.

Роди тели купили коробку с карамелью для учеников. В коробке было 320 штук карамели.  карамели раздали ученикам. Учителю дали  от всей коробки. Остальную карамель оставили не пришедшим ученикам. Сколько оставили карамели не пришедшим ученикам?

1) 320:8=40 (шт)

2) 40*7=280 (шт) раздали ученикам

3) 320:32=10 (шт)

4) 280+10=290 (шт) отдали учителю

5) 320-290=30 (шт) осталось карамели

Ответ: 30 штук карамели оставили не пришедшим ученикам.

Стимулирующие приемы:

- решение пройденной задачи. Этот стимулирующий прием используется, для того, чтобы учащиеся смогли увидеть, вспомнить ошибки, которые они допустили в предыдущей задаче и сделать выводы из своих ошибок, не применяя в новой похожей задаче.

- построение вместе с учащимися схемы к задаче. Данный стимулирующий прием позволяет наглядно увидеть последовательность решения задачи, увидеть скрытые, на первый взгляд, действия, которые необходимо совершить в процессе поиска решения.

- оформление задачи наглядным материалом. В данной задаче наглядным материалом послужили: изображение карамели, числовой луч из ватмана, где дети искали части целого. Данный стимулирующий прием является необходимым, он способствует более внимательному рассмотрению детьми задачи; проявляется интерес к поиску решения.

Задача 2.

Прочитайте задач. 1)составьте к задаче краткую запись. 2)решение с пояснением. 3)полный ответ.

Торт разделили на 15 равных частей.  съела Нина.  съел Миша. То, что съел Миша - это в 3 раза больше, чем съела Маша. Остальную часть торта оставили на завтра. Какую часть торта оставили на завтра? (ответ дробью).

1) 15:3= 5 – съела Нина.

2) 15:5*2=6 – съел Миша.

3) 6:3=2 – съела Маша.

4)15- (5+6+2) = 2 – оставили на завтра.

Ответ: 2/15 части торта оставили на завтра.

Стимулирующие приемы:

- решение пройденной задачи.

- построение вместе с учащимися схемы к задаче.

- оформление содержания задачи наглядным материалом. В данной задаче наглядным материалом послужило изображении торта, состоящее из 15 равных частей, которые можно прикрепить магнитами к доске, что удобно, когда нужно показать процесс вычитания или сложения частей.

3. Контрольный эксперимент.

Контрольный эксперимент проводится с целью: сравнить результаты решения задач проводимые на контрольном этапе экспериментальной работе с результатами, полученными в ходе констатирующего эксперимента, где не применялись ни какие стимулирующие приемы.

Критерии оценки остались прежними.

Так же как и на предыдущих этапах эксперимента, были даны 2 типа задач с дробями: прямая и косвенная форма. Эксперимент проводился в течении 2 дней.

В ходе решения задачи были введены уже подтвердившие свою результативность стимулирующие приемы для 2 типов задач, такие как:

- решение пройденной задачи.

- построение вместе с учащимися схемы к задаче.

- оформление содержания задачи наглядным материалом.

Также были применены и новые стимулирующие приемы:

- материальное поощрение;

- моральное поощрение.

Задача 1.

Прочитайте задач. 1)составьте к задаче краткую запись. 2)решение с пояснением. 3)полный ответ.

Юле подарили 135 конфет.  частью всех конфет она поделилась с Антоном. Из тех конфет, которыми поделилась Юля с Антоном  были карамельными, а остальные шоколадными. Антон поделился  своих шоколадных конфет с Ваней. Конфеты Ване показались вкусными. Каким количеством конфет поделился с Ваней Антон?

1) 135:5*2=54 (конф) – количество конфет с которыми поделилась Юля с Антоном.

2) 54:2=27 (конф) – количество шоколадных конфет Антона

3) 27:3=9 (конф) – Ванины конфеты

Ответ: Антон поделился 9 конфетами с Ваней.

Стимулирующие приемы:

- решение пройденной задачи.

- построение вместе с учащимися схемы к задаче.

- оформление содержания задачи наглядным материалом.

- материальное поощрение. В качестве материального поощрения были конфеты, которые раздавались всем, кто решит задачи с поставленными перед ними вначале условиями - это 1) Краткая запись. 2) Решение с пояснением. 3) Полный ответ.

- моральное поощрение. В виде похвалы за выполненную работу.

Задача 2.

Прочитайте задач. 1)составьте к задаче краткую запись. 2)решение с пояснением. 3)полный ответ.

На Новый Год в подарочном наборе было 36 конфет - это в 2 раза меньше чем штук печенья из этого же подарочного набора.  печенья съел Дима. печенья съел Витя. Остальное печенье съела Маша. Какое количество печенья съела Маша.

1) 36*2=72 (шт) – количество печенья

2) 72 : 3=24 (шт) – съел Дима

3) 72 : 4 * 2= 36 (шт) – съел Витя

4) 72 – (36+24) = 12 (шт) – съела Маша

Ответ: 12 штук печенья съела Маша.

Стимулирующие приемы:

- решение пройденной задачи.

- построение вместе с учащимися схемы к задаче.

- оформление содержания задачи наглядным материалом.

- материальное поощрение. В качестве материального поощрения были конфеты, которые раздавались всем, кто решит задачи с поставленными перед ними вначале условиями - это 1) Краткая запись. 2) Решение с пояснением. 3) Полный ответ.

- моральное поощрение. В виде похвалы за выполненную работу.

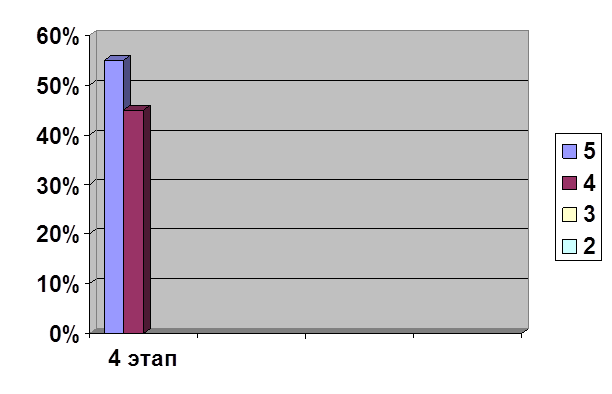
Контрольный эксперимент показал следующие результаты.

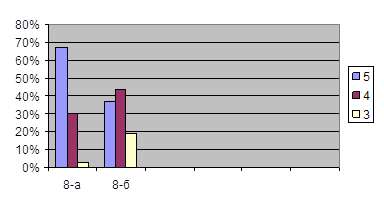
Прямая форма задачи: из 23 учеников на «5» решили 16 чел. (70%), на «4» - 3 чел. (12%), на «3» - 2 чел. (9%), «2» - 2 чел. (9%).

Косвенная форма задачи: из 23 учеников на «5» решили 15 чел. (66%), на «4» - 4 чел. (17%), на «3» - 3 чел. (13%), «2» - 1 чел. (4%).

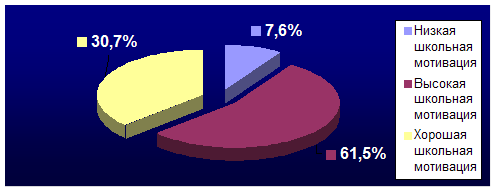
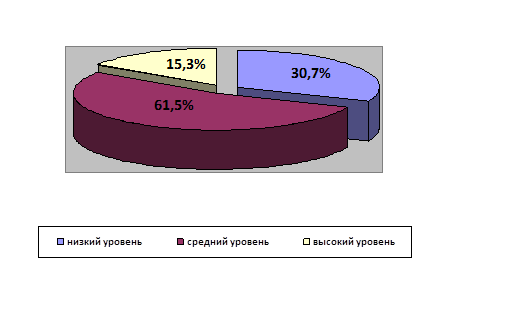
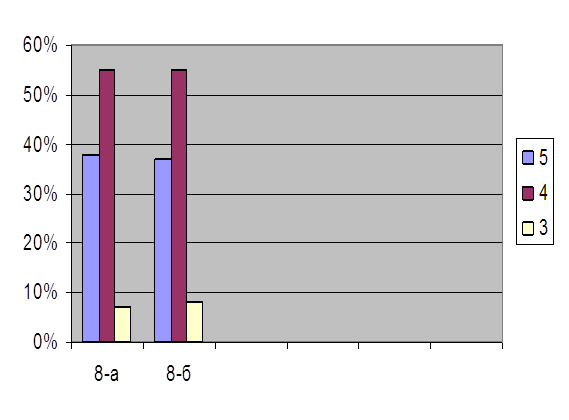
Результаты эксперимента приведены в таблице 2 и на рис. 6 и рис. 7

(см. Приложение 4).

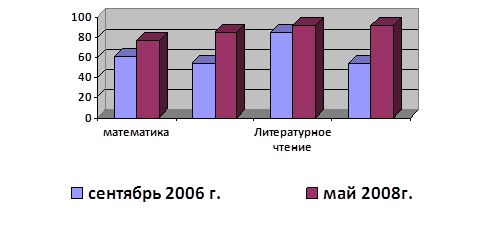
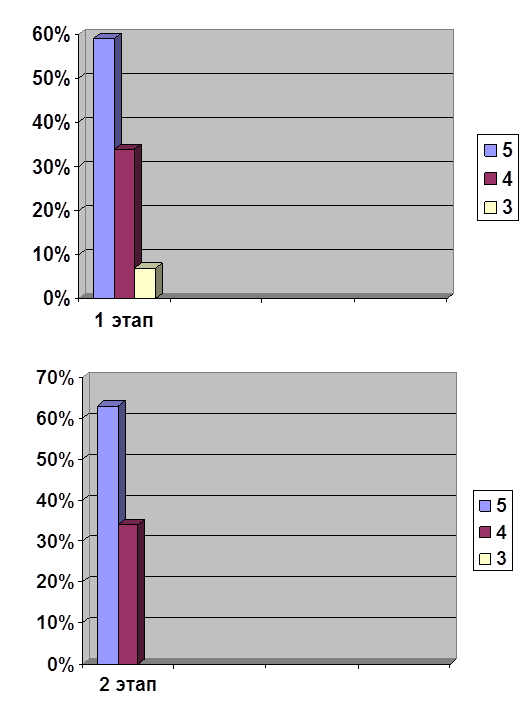
Для прослеживания динамики влияния стимулирующих приемов на процесс поиска решения задачи показаны на рис. 8 (по прямым формам) и рис. 9 (по косвенным формам) (см. Приложение 5)

По результатам проведенных формирующих и контрольных экспериментов было установлено:

Поэтапное применение стимулирующих приемов положительно сказываются на процент качества решения задачи с дробями.

В прямой форме задаче с дробями, процент решений на «5» увеличилось на 22%. В данном виде задач прослеживается соответственно динамика уменьшения процента по оценкам «2», «3» и «4», что видно на гистограмме рис. 8. (см. приложение 5).

В косвенной форме задаче с дробями, так же процент решений на «5» увеличился по сравнению с результатами констатирующего эксперимента и составил 22%. Так же как и в прямой форме здесь прослеживается динамика уменьшения процента по оценкам «2» и «3», но процент решенных задач на оценку «4» не уменьшается, а держится на одинаковом уровне, это позволяет говорить, что данный тип задач не совсем удается учащимся, вызывают затруднения подобная форма задачи с дробями. рис. 9. (см. приложение 5).

Сравнительный анализ по двум формам задачи с дробями показал, что стимулирующие приемы положительно влияют и дают большой положительный процент правильных решений.

Таким образом, основываясь на результатах проведения опытно-экспериментальной работы по использованию стимулирующих приемов в процессе поиска решения задач с дробями, можно с уверенностью утверждать, что применение указанных стимулирующих приемов в обучении младших школьников не только обоснованно, но и необходимо с целью повышения эффективности усвоения знаний, а также активизации интереса к учебному материалу.

Заключение

В данной работе были рассмотрены вопросы стимулирования математической деятельности младших школьников в процессе поиска решения задач с дробями.

Теоретические и практические вопросы использования стимулирующих приемов в процессе обучения математики младших школьников и в частности в процессе решения задач остаются открытыми и не теряют своей актуальности.

В школе учителями активно оказывается стимулирующая помощь учащимся, но большое внимание целенаправленному использованию стимулирующих приемов в процессе поиска решения задач с дробями не уделяют.

В ходе исследования были решены все поставленные задачи:

1) На основе анализа психолого-педагогической и методической литературы по данной проблеме было выявлено, что целенаправленное применение стимулирующих приемов в процессе поиска решения задач имеет большое значение для повышения уровня знаний учащихся, расширения кругозора, мотивацию, развития всех психических функций и т.п.

2) Основываясь на анализе педагогической литературы и учебников по математике для начальной школы, был подобран комплекс стимулирующих приемов, которые были применены в процессе поиска решения задач с дробями.

Были применены следующие стимулирующие приемы:

- решение пройденной задачи.

- построение вместе с учащимися схемы к задаче.

- оформление содержания задачи наглядным материалом.

- материальное поощрение.

- моральное поощрение.

3) Экспериментально была доказана эффективность подобранных стимулирующих приемов в процессе поиска решения задач с дробями, а так же их положительное влияние на усвоение темы связанной с дробями.

Гипотеза исследования была подтверждена. Практическая значимость работы заключается в том, что подобранный комплекс стимулирующих приемов доказал свою эффективность и безусловно применим при решении младшими школьниками задач с дробями.

Список литературы

Бабанский, Ю.К. Педагогика: Учебное пособие для студентов педагогических институтов. - М.: Просвещение, 1983.

Баранова, Е.В, Как увлечь школьников исследовательской деятельностью. // Математика в школе. – 2004. - № 2. – С.7-10. ISBN 5-9219-0288-8

Белкин, A.С. Ситуация успеха. Как ее создать. - М., 1991. – 169 с.

Бенерджи, Р. Теории решения задач. - М.: Мир, 1972. – 224 с.

Божович, Л.И. Личность и ее формирование в детском возрасте. – М.: Педагогика, 1968. - 191 – 201 с.

Выгодский, Л. С. Педагогическая психология. - М., 1996. – 201 с.

Гамезо, Л.И. Возрастная и педагогическая психология: Учебник. – М.: Наука, 1984. -256 с.

Дусавицкий, А.К. Формирование мотивов учения в школьном возрасте. - М.: Просвещение, 1983. – 64 с.

Дусавицкий, А.К. Формула интереса. — М., 1989. - 69 с.

Егошина, Е. В. Методика исследования мотивов учения // Начальная школа. - 1995. - № 5. – С. 15. ISBN 5-9571-0097-8

Засенок, В.П. Эвристические приемы решения логических задач. // Математика в школе. – 2005. - № 3. – С.29-33. ISBN 5-88527-257-3

Ильин, Е.П. Мотивация и мотивы.: Учебное пособие – СПБ.: Питер., 2000. – 512 с. – (Мастера психологии). ISBN 5-272-00028-5

Колягин, Ю.М. Методика преподавания математики в средней школе. Общая методика / Под. ред. Ю.М.Колягина, В.А.Оганесяна, В.Я.Санинский, Г.Л.Луканкин. - М.: Просвещение, 1980. - 169 с.

Леонтьев А.Н. Проблемы развития психики. – М., 1972. С. 513

Божович Л.И. Личность и ее формирование в детском возрасте. – М.: Просвещение. 1968. – 249 с.

Божович Л.И. Личность и ее формирование в детском возрасте. – М.: Просвещение, 1968. - 213-214 с.

Морозова Н.Г. Учителю о познавательном интересе // Психология и педагогика. - 1979г. - №2. – С.5.

Щукина Г.И, Активация познавательной деятельности учащихся в учебном процессе. – М.: Питер, 1979. - 97 с.

Щукина Г.И. Проблема познавательного интереса в педагогике. – М.: Питер, 1971. - 29 с.

Леонтьев, А. Н. Потребности, мотивы и эмоции. - М., 1971. – 38 с.

Леонтьев, А.Н. Деятельность. Сознание. Личность. – М.: Просвещение, 1982. – 84 с.

Леонтьев, А.Н. Проблемы развития психики. – М.: Просвещение, 1972. – 513 с.

Маркова, А.К. Мотивация учения и ее воспитание у школьников / Под ред. А.К.Марковой, А.Б.Орлова, Л.М.Фридмана. - М.: Педагогика, 1983. - 64 с.

Маркова, А.К. Формирование мотивации учения: Книга для учителя. – М.: Просвещение, 1990. – 144 с.

Менчинская, М.А. Проблемы учения и развития. Советская педагогика. - 1979. - № 3. - С. 15

Моро, М.И. Методика обучения математике в 1-3 классах. Пособие для учителя. Изд. 2-е, перераб. и доп. / М.И.Моро, А.М.Пышкало. - М.: «Просвещение», 1978. - 336 с.

Морозова, Н.Г. Учителю о познавательном интересе // Психология и педагогика, 1979. - №2. – С.35.

Мотивы познавательной деятельности / Под ред. Ю.Н.Кулюткина, Г.С.Сухобской. – М.: Просвещение, 1972.

Немов, Р.С. Психология. Учебник. – М.: Просвещение: ВЛАДОС, 1995. – 573 с. ISBN 5-691-00233-3

Нильсон, Н. Искусственный интеллект. Методы поиска решений. - М.: Мир, 1973. – 495 с.

Подласый, И.П. Педагогика начальной школы: Учеб. пособие для стул. пед. колледжей. - М.: Гуманит. изд. центр ВЛАДОС, 2000. - 400 с. ISBN 5-691-00533-2

Поиа, Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание. - М.: Наука, 1976. – 178 с.

Равкин, З.И. Педагогическое стимулирование нравственного развития и познавательной активности школьников: – Киров, - Йошкар-Ола: КГПИ, 1975. - 45 с.

Равкин, З.И. Проблемы педагогического стимулирования и методологии исследований истории советской школы. - Йошкар-Ола: МШИ, 1972. - 25 с.

Равкин, З.И. Проблемы стимулирования активности учащихся в процессе нравственного воспитания и обучения: - Йошкар-Ола: МГПИ, 1974. - 50 с.

Рузин, Н.К. Методика обучения и стимулирование поисковой деятельности учащихся по решению школьных математических задач: Учебное пособие. - Горький: ГГПИ им. М. Горького, 1989. - 80 с.

Рузин, Н.К. Методы обучения математике / Под. ред. Б.С.Каплан, Н.К.Рузина, А.А.Столяра. - Минск: Народная газета, 1981. – 300 с.

Скаткин, М.Н. Дидактика средней школы. - М.: Просвещение, 1982. – 323 с.

Сохор, А.М. Логическая структура учебного материала. - М.: Педагогика, 1974. – 192 с.

Столяр, А.А. Педагогика математики. – Минск.: Высшая школа, 1974. – 169 с.

Уинстон, И. Искусственный интеллект. - М.: Мир, 1980. – 512 с.

Формирование мотивации учения / Под ред. А.К.Марковой, Т.А.Матис, А.Б.Орлова. - М., 1990. – 192 с.

Шуман, В.П. Актуальные вопросы дидактики. Проблемы стимулирования познавательной деятельности учащихся. - Ч. 1. -Владимир: ВГПИ, 1974.

Ссылки:

Педагогические проблемы становления субъектности школьника, студента, педагога в системе непрерывного образования: Сб. науч. и метод. тр. Вып. 2 / Под ред. ред. Н. К. Сергеева, Н. М. Борытко. Волгоград: Изд-во ВГИПКРО, 2001. 80 с.

Глава 2.3. Стимулироване интеллектуальной инициативы учащихся в процессе решения задач. В. Г. Денисова http://borytko.nm.ru/papers/subject2/denisova.htm

Сайт Сахалинского государственного университета. Роль решения задач в развитии логического мышления младших школьников/ Мальцева И.Н. http://www.sakhgu.sakhalin.ru/document.php?language=rus&id=vestnik/poiv/s2

Горно-Алтайский государственный университет. Пособие для подготовки учащихся к математической олимпиадам. Учебное пособие 2005г. Составители: Деев Михаил Ефимович, кандидат физ.-мат. наук, доцент ГАГУ; Соловьев Сергей Петрович, кандидат физ.-мат. наук, доцент ГАГУ; Соловьева Любовь Алексеевна, старший преподаватель ГАГУ. Глава I . Задачи и их решение http://e-lib.gasu.ru/eposobia/de