Навигация
Построение кривой разгона
1 Построение кривой разгона
Кривой разгона называют процесс изменения во времени выходной переменной, вызванный ступенчатым входным воздействием. Кривая разгона служит для определения динамических свойств объекта.
Запаздывание объекта выражается в том, что его выходная величина начинает изменяться не сразу после нанесения возмущения, а только через некоторый промежуток времени, называемым временем запаздывания.
Под постоянной времени объекта понимается время, в течение которого выходная величина достигла бы своего нового установившегося значения, если бы она изменялась с постоянной скоростью, равной скорости ее изменения в начальный момент времени.
Коэффициент передачи объекта представляет собой изменение выходной величины объекта при переходе из начального в новое установившееся состояние, отнесенное к изменению возмущения на входе [1].
Снятие кривой разгона предусматривает нанесение на объект ступенчатого возмущения путем энергичного изменения степени открытия проходного сечения регулирующего органа, при этом отмечают величину и момент нанесения возмущения. Изменения выходной величины регистрируют до тех пор, пока объект не примет установившееся значение.
Кривая разгона отличается от переходной характеристики тем, что амплитуда «скачка» может быть произвольной, в то время как переходная характеристика есть реакция объекта управления на единичный скачок по управляющей переменной [2].
Кривая разгона получается пересчетом безразмерной кривой разгона по формулам
t = Mt. tб
Δy = My. Δyб
где t – реальное время,
tб – безразмерное время,
Mt – масштаб времени,
My – масштаб регулируемой переменной,
Δy – изменение регулируемой переменной в натуральных единицах,
Δyб – изменение регулируемой переменной в безразмерном виде
Рассчитаем кривую разгона (таблица 2)
Таблица 2 – Пересчитанная кривая разгона
| t, мин | 0 | 2,4 | 4,8 | 7,2 | 9,6 | 12 | 14,4 |
| Δy, мм.в.ст. | 0 | 0,043 | 0,301 | 1,075 | 1,849 | 2,494 | 3,01 |
| t, мин | 16,8 | 19,2 | 21,6 | 24 | 26,4 | 28,8 | 31,2 |
| Δy, мм.в.ст. | 3,354 | 3,612 | 3,784 | 3,913 | 4,042 | 1,128 | 4,171 |
| t, мин | 33,6 | 36 | 38,4 | 40,8 | 43,2 | 45,6 | |
| Δy, мм.в.ст. | 4,214 | 4,2355 | 4,257 | 4,3 | 4,3 | 4,3 |
Кривая разгона представлена на рисунке 1.
Определим параметры аппроксимации кривой разгона. Касательная касается кривой разгона в точке А1, соответствующей максимальной крутизне.
В соответствии с рисунком 1 коэффициент передачи равен
Коб = Δyуст / ΔU
Коб = 4,3 / 8 = 0,54 мм.в.ст./%
где Δyуст – установившееся значение выходной переменной,
ΔU – изменение входной переменной.
Передаточная функция данной аппроксимации будет иметь вид
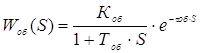
![]()
где Коб – коэффициент передачи объекта,
Тоб – постоянная времени (Тоб = 18 – 4 = 14 мин),
τоб – время запаздывания, (τоб = 4 мин),
S – переменная Лапласа.
2 Определение передаточной функции методом площадей
Передаточная функция второго порядка может быть представлена в следующем виде

Коэффициенты а1 и а2 вычисляются по формулам
а1 = F1 = Δt {∑ [1-Δyб (Δt . i)] – 0,5},
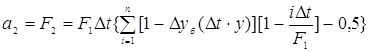
где n – количество интервалов разбиения кривой разгона (n=19),
Δt – интервал разбиения (Δt = Мt = 2,4 мин),
Δyб (t . i) – значение безразмерной кривой разгона в i-й момент времени.
Тогда
а1 = F1 = 2,4{ (1-0) + (1 – 0,1) + (1 – 0,07) + (1 – 0,25)+(1 – 0,43)+(1 – 0,58) + (1 – 0,7) + (1 – 0,78) + (1 – 0,84) + (1 – 0,88) + (1 – 0,91) + (1 – 0,94)
+ (1 – 0,96) + (1 – 0,97) + (1 – 0,98) + (1 – 0,985) + (1 – 0,99) – 0,5 }=
= 2,4 . 5,225 = 12,54 мин
![]()
![]()
![]()
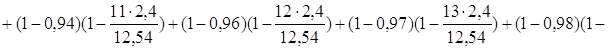
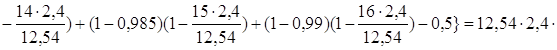
![]() мин 2
мин 2
Передаточная функция второго порядка будет иметь вид

Определение передаточной функции методом площадей является более сложным по сравнению с определением по кривой разгона. Однако передаточная функция второго порядка имеет более точное представление.
0 комментариев