Вычисление настроек регуляторов и исследование статических свойств системы регулирования

3 Вычисление настроек регуляторов и исследование статических свойств системы регулирования

Автоматическое устройство, обеспечивающее поддержание выходных величин объекта вблизи требуемых значений, называют автоматическим регулятором.

Регулятор реализует закон регулирования. Структурная схема системы регулирования представлена на рисунке 2.

			Р – регулятор, ОУ – объект управления,

Рисунок 2 – Структурная схема системы регулирования

Целью регулирования является выполнение условия ε = y₃ – y = 0

Основные законы регулирования:

1) релейный (р- закон)

0, если ε ≤0

U = 1, если ε>0

где 1 – включено, 0 – выключено

Преимущество: простота реализации, недостаток: низкое качество регулирования.

2) пропорциональный (п-закон)

U = К_П^. ε

где К_П – коэффициент передачи регулятора.

Преимущества: простота реализации, высокое быстродействие, недостатки: ненулевая ε, низкое качество регулирования.

3) Интегральный (И-закон)

,

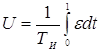где Т_И – постоянная интегрирования.

Преимущества: отсутствие ошибки в установившемся режиме, недостатки: низкое быстродействие и склонность к автоколебаниям.

4) Пропорционально-интегральный (ПИ-закон)

Обладает преимуществами П- и И- регуляторов. Недостаток: сложность.

Определим К_П для П-регулятора по формуле

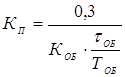
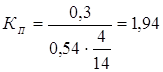
Для ПИ- регулятора

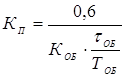
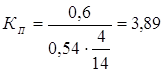
Т_И = 0,6 ^. Т_ОБ = 0,6 ^. 14 = 8,4 мин

Для определения статической ошибки системы регулирования нужно изобразить эту систему, содержащую регулятор К_П и объект К_ОБ (рисунок 3).

Рисунок 3 – Структурная схема замкнутой системы регулирования

Коэффициент передачи последовательного соединения звеньев равен

К₁ = К_П^. К_ОБ

Коэффициент передачи обратной связи К₂ = 1

Коэффициент передачи замкнутой системы в статике

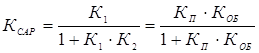
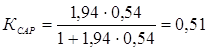
Принимая величину изменения задания y_З = 1, находим установившееся значение

y_уст = 1 ^. 0,51 = 0,51

Тогда статическая ошибка равна

Для уменьшения статической ошибки и сохранения других показателей качества регулирования необходимо применять другие законы регулирования (например И- или ПИ- закон).

4 Исследование устойчивости системы регулирования

Под устойчивостью понимают свойство системы самостоятельно возвращаться к равновесному состоянию после снятия возмущения, нарушевшего ее равновесие.

Устойчивость линейной системы определяется характером его свободного движения, которое описывается однородным дифференциальным уравнением

При вещественных корнях решение имеет вид

y(t)= c₁^. e^P1t + c₂^. e^P2t + …+ c_n^. e^Pnt ,

где c_n – постоянная интегрирования

p_n – корни характеристического уравнения

a_n^. p_n + a_n-1^. p^n-1 + …+a₀ = 0

Для устойчивой работы системы необходимо, чтобы P_i<0

Решение характеристического уравнения сложно, поэтому разработаны другие критерии устойчивости.

Частотным критерием Найквиста определяют устойчивость замкнутой системы по поведению соответствующей ей разомкнутой системы.

Если в разомкнутом состоянии система устойчива и ее амплитудно-фазовая характеристика (АФХ) при изменении частоты W от нуля до бесконечности не охватывает на комплексной плоскости точку с координатами (-1;0), то система в замкнутом состоянии будет устойчива. АФХ охватывает точку, если точка лежит внутри контура, образованного характеристиками и отрезками действительной оси, соединяющей точки ноль и бесконечность.

Выполним исследование системы на устойчивость. Определим АФХ разомкнутой системы с П-регулятором. Для получения передаточной функции приведем рисунок 4.

Рисунок 4 – Функциональная схема разомкнутой системы регулирования

Передаточная функция разомкнутой системы будет иметь вид

W_РАЗ(S) = W_P (S) ^. W_ОБ (S)

Выполняя замену W_Р = К_П, W_ОБ (S) = j w получим

Избавляясь от мнимости в знаменателе, получим АФХ в алгебраической форме

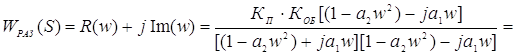
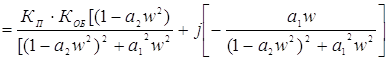
Подставляя в полученное выражение численные значения, получим АФХ для исследования устойчивости

 

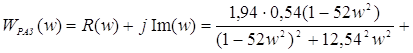
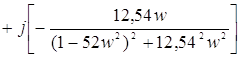
Для исследования устойчивости нужно построить годограф АФХ, для чего выполним вычисление R(w) и Im(w) для различных w. Результаты вычислений сведем в таблицу 3.

Таблица 3 – Расчет АФХ разомкнутой системы

w, мин	R(w)	Im(w)	w, мин	R(w)	Im(w)
0	1,05	0	0,10	0,28	-0,69
0,01	1,04	-0,12	0,11	0,19	-0,68
0,02	1,00	-0,25	0,12	0,11	-0,65
0,03	0,95	-0,36	0,13	0,05	-0,61
0,04	0,88	-0,46	0,14	-0,01	-0,57
0,05	0,79	-0,55	0,15	-0,05	-0,52
0,06	0,69	-0,61	0,20	-0,15	-0,34
0,07	0,59	-0,66	0,30	-0,14	-0,14
0,08	0,48	-0,69	0,40	-0,10	-0,06
0,09	0,38	-0,70	0,50	-0,07	-0,03

По результатам расчетов строим годограф (рисунок 5). Из рисунка видно, что система в замкнутом состоянии будет устойчива.