Вариант 6
Тема: Алгебра матриц
Задание: Выполнить действия над матрицами.
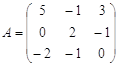
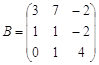
1) С=3A-(A+2B)B
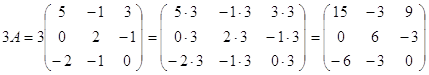
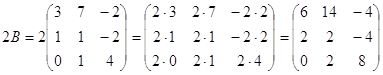
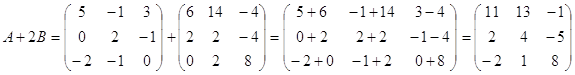
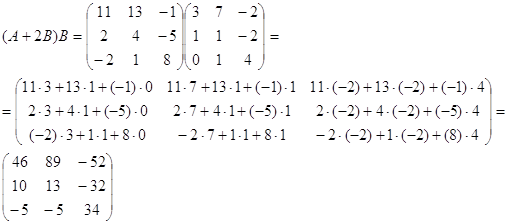
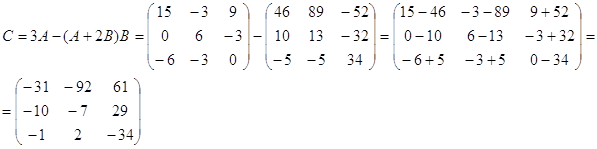
2) D=A2+B2+4E2
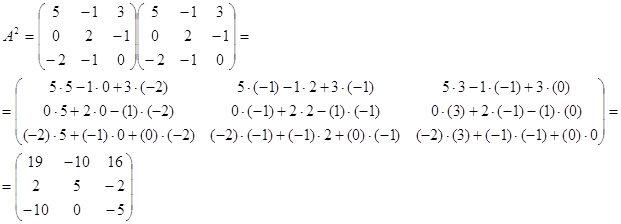
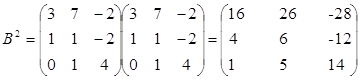
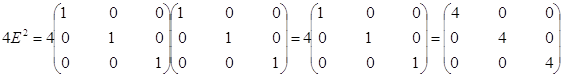
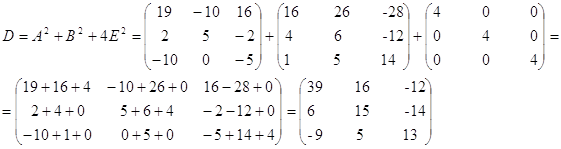
Тема: Обращение матриц
Обратить матрицу по определению:
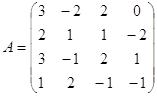
Определитель матрицы:
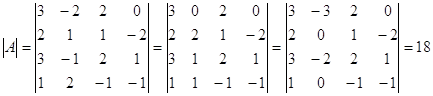
Далее находим матрицу алгебраических дополнений (союзную матрицу):
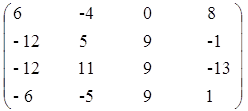
Обратную матрицу находим:
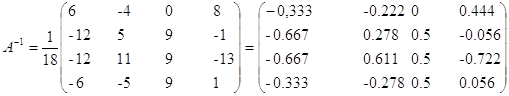
По определению обратной матрицы:
![]()
Действительно:
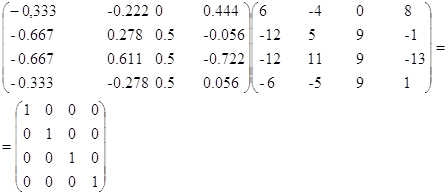
Тема: решение матричных уравнений
Задание 1: Решить матричное уравнение:
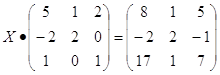
Решение.
Нахождение столбца Х сводится к умножению матрицы на обратную:
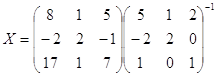
Матрица коэффициентов А:
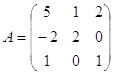
Найдем обратную матрицу A-1:
Определитель матрицы A:
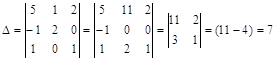
Алгебраические дополнения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Транспонированная матрица алгебраических дополнений:
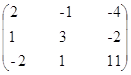
Запишем выражение для обратной матрицы:
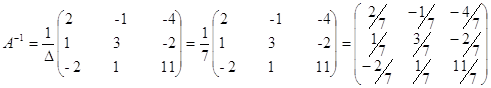
Итак, выполняем умножение матриц и находим матрицу X:
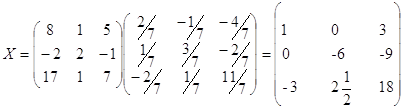
Ответ:
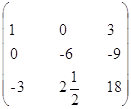
Задание 2: Решить систему уравнений матричным способом
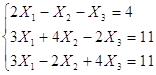
Решение
Матричная запись уравнения:
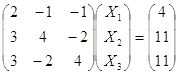
Матрица коэффициентов А:
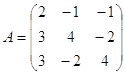
Найдем обратную матрицу A-1:
Определитель матрицы A:
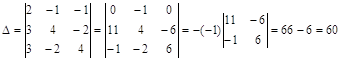
Алгебраические дополнения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Транспонированная матрица алгебраических дополнений (союзная матрица):
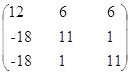
Запишем выражение для обратной матрицы:
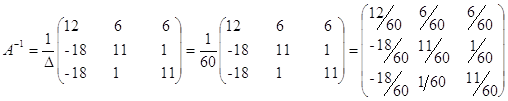
Вычислим столбец неизвестных:
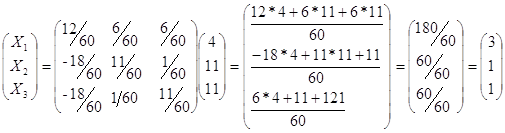
Тема: Решение систем линейных уравнений методом Крамера и Гаусса
Задание 1: Исследовать и решить систему по формулам Крамера:
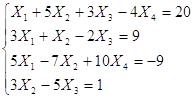
Найти решение системы уравнений по методу Крамера.
Согласно методу Крамера, если определитель матрицы системы ненулевой, то система из 4-х уравнении имеет одно решение, при этом значение корней:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
Где:
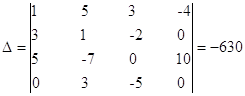 - определитель матрицы коэффициентов – ненулевой.
- определитель матрицы коэффициентов – ненулевой.
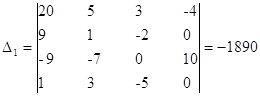 - определитель матрицы полученной путем замены первого столбца матрицы коэффициентов на столбец свободных членов.
- определитель матрицы полученной путем замены первого столбца матрицы коэффициентов на столбец свободных членов.
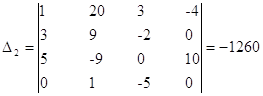 - определитель матрицы полученной заменой второго столбца матрицы коэффициентов на столбец свободных членов.
- определитель матрицы полученной заменой второго столбца матрицы коэффициентов на столбец свободных членов.
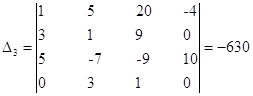 - определитель матрицы полученной заменой третьего столбца матрицы коэффициентов на столбец свободных членов.
- определитель матрицы полученной заменой третьего столбца матрицы коэффициентов на столбец свободных членов.
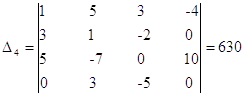 - определитель матрицы полученной заменой четвертого столбца матрицы коэффициентов на столбец свободных членов.
- определитель матрицы полученной заменой четвертого столбца матрицы коэффициентов на столбец свободных членов.
Итак:
![]()
![]() ,
,
![]() ,
,
![]() .
.
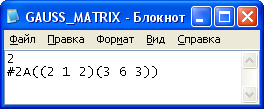
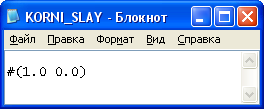
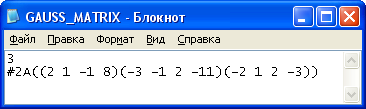
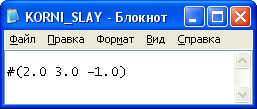
Задание 2: Решить эту систему по методу Гаусса.
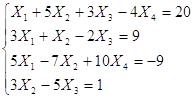
Метод Гаусса заключается в сведении системы к треугольному виду.
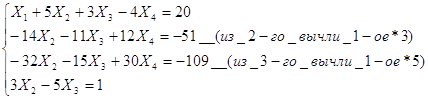
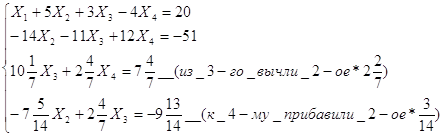
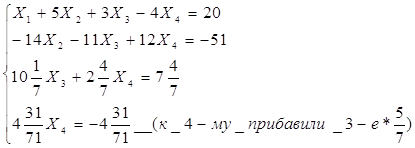
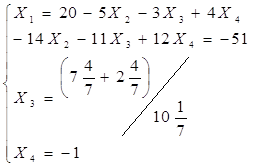
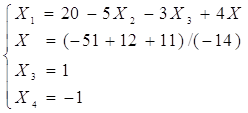
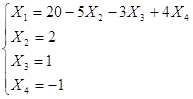
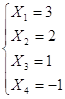
Видим, что решение системы по методу Гаусса совпадает с решением по методу Крамера.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
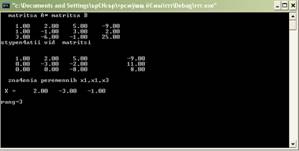
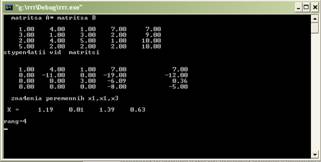
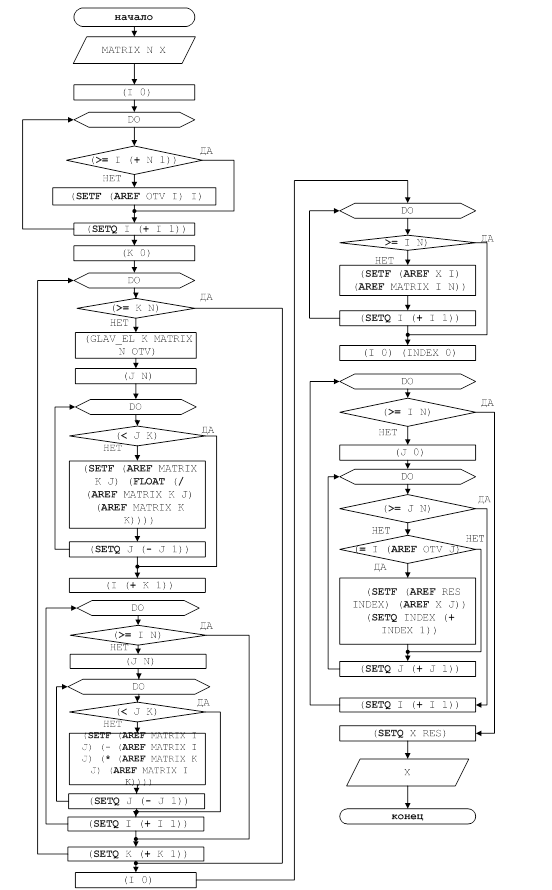
... 4.Исходный текст программы Составить программу решения систем линейных алгебраических уравнений с квадратной невырожденной матрицей порядка n методом Гаусса с использованием языка С++ . // Решение системы линейных уравнений методом Гаусса. #include<io.h> #include "stdio.h" #include "conio.h" #include <windows.h> #include <iostream> #include <time.h> #include ...
... + аm2с2 + …+ аmnсn где c1, c2,..., сп — коэффициенты линейных комбинаций. Таким образом, системе (14) удовлетворяют значения x1 = c1,..., хп = сп, следовательно, она совместна. Теорема доказана. Доказанная теорема совместности системы линейных уравнений называется теоремой Кронекера – Капелли. Пример 1. Рассмотрим систему 5x1 – x2 + 2x3 + x4 = 7; 2x1 + x2 – 4x3 – 2x4 = 1; x1 – 3x2 + ...
... треугольной матрицей. Вычисления значений неизвестных производят на этапе обратного хода. Целью данной курсовой работы является численное решение системы линейных уравнений с помощью метода исключения Гаусса с выбором главного элемента по столбцу. 1 Постановка задачи Задача ставится следующим образом. Пусть требуется найти решение системы линейных алгебраических уравнений a1,1x1 + a1, ...

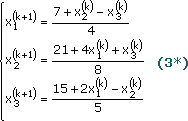
0 комментариев