Навигация
Уравнение малых поперечных колебаний струны
2.1 Уравнение малых поперечных колебаний струны.
Каждую точку струны l можно охарактеризовать значение её абсциссы x. Описание процесса колебания струны может быть проведено при помощи задания положения точек струны в момент времени t достаточно задать компоненты вектора смещения {u1 (x,t), u2(x,t), u 3(x,t)} точки x в момент t.
Будем предполагать, что смещения струны лежат в одной плоскости (x,u) и что вектор смещения u перпендикулярен в любой момент к оси x; тогда процесс колебания можно описать одной функцией u(x,t), характеризующей вертикальное перемещение струны. Будем рассматривать струну как гибкую упругую нить. Математической выражение понятия гибкости заключается в том, что напряжения, возникающие в струне, всегда направлены по касательной к ее мгновенному профилю (рис. 1). Это условие выражает собой то, что струне не сопротивляется изгибу.
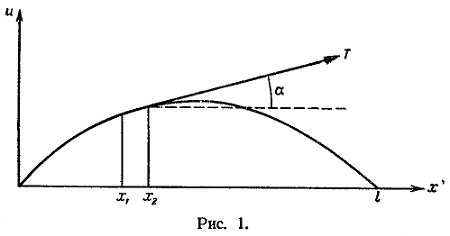
Величина натяжения, возникающего в струне вследствие упругости, может быть вычислена по закону Гука. Будем рассматривать малые колебания струны и пренебрегать квадратом ux по сравнению с единицей.
Пользуясь этим условием, подсчитаем удлинение, испытываемое участком струны (x1 ,x2). Длина дуги этого участка равна
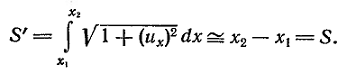
Таким образом, в пределах принятой нами точности удлинения участков струны в процессе колебания не происходит; отсюда в силу закона Гука следует, что величина натяжения T в каждой точке не меняется со временем. Покажем также, что натяжение не зависит и от x, т. е.
![]()
Найдем проекции натяжения на оси x и u (обозначим их Tx и Tu):
![]()
![]()
где α – угол касательной к кривой u(x,t) с осью x. На участок (x1, x2) действуют силы натяжения, внешние силы и силы инерции. Сумма проекции всех сил на ось x должна быть равна нулю (мы рассматриваем только поперечные колебания). Так как силы инерции и внешние силы по предположению направлены вдоль оси u, то
![]() (1)
(1)
Отсюда в силу произвольности x1 и x2 следует, что натяжение не зависит от x, т. е. для всех значений x и t
![]() (2)
(2)
Перейдем к выводу уравнения поперечных колебаний струны. Воспользуемся вторым законом Ньютона. Составляющая количества движения участка струны (x1, x2) по оси u равна
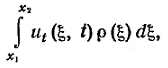
где ρ – линейная плотность струны. Приравняем изменение количества движения за промежуток времени ∆t = t2 - t1
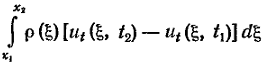
импульсу действующих сил, складывающихся из натяжения
![]()
в точках x1 и x2 и внешней силы, которую будем считать непрерывно распределенной с плотностью (нагрузкой) F(x, t), рассчитанной на единицу длины. В результате получим уравнение поперечных колебаний элемента струны в интегральной форме
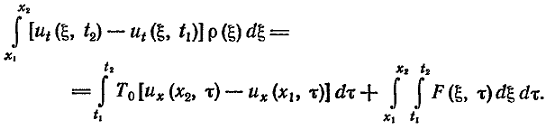 (3)
(3)
Для перехода к дифференциальному уравнению предположим существование и непрерывность вторых производных от u(x, t). Тогда фотмула (3) после двукратного применения теоремы о среднем примет вид
![]()
где
![]()
Сократим на ∆x∆t и переходя к пределу при x2→x1, t2→t1, получим дифференциальное уравнение поперечных колебаний струны
![]() (4)
(4)
В случае постоянной плотности ρ = const этому уравнению обычно придают вид
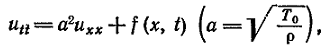 (5)
(5)
где
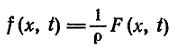 (6)
(6)
есть плотность силы, отнесенная к единице массы. При отсутствии внешней силы получим однородное уравнение
![]()
или
![]()
описывающее свободные колебания струны. Это уравнение является простейшим примером уравнения гиперболического типа.
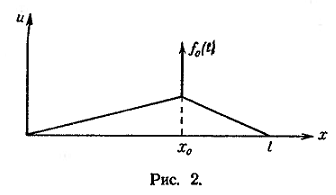
Если в точке x0(x1<x0<x2) приложена сосредоточенная сила f0(t) (рис. 2), то уравнение (3) запишется так:
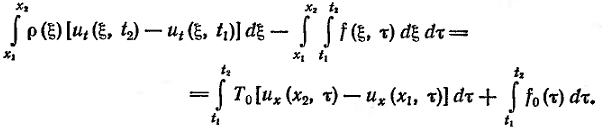
Поскольку скорости точек струны ограничены, то при x1→x0 и x2→x0интегралы в левой части этого равенства стремятся к нулю, и равенство (3) принимает вид
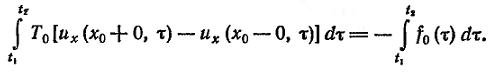 (7)
(7)
Пользуясь теоремой о среднем, сокращая обе части равенства на ∆t и переходя к пределу при t2→t1 получим:
![]()
Отсюда видно, что в точке приложения сосредоточенной силы первые производные претерпевают разрыв и дифференциальное уравнение теряет смысл. В этой точке должны выполняться два условия сопряжения
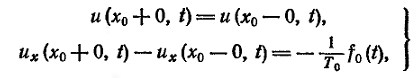 (8)
(8)
второе из которых выражает непрерывность струны, второе определяет величину излома струны в точке x0, зависящую от f0(t) и натяжения T0.
Теперь рассмотрим задачу о поперечных колебаниях струны, закрепленной на концах. В этой задаче u(x, t) дает отклонение струны от оси x. Если концы струны 0 ≤ x ≤ l закреплены, то должны выполняться «граничные условия»
u(0, t) = 0, u(l, t) = 0.
Так как процесс колебания струны зависит от её начальной формы и распределения скоростей, то следует задать «начальные условия»:
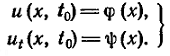
Таким образом, дополнительные условия состоят из граничных и начальных условий, где φ(x) и ψ(x) – заданные функции точки.
Эти условия вполне определяют решение уравнения колебания струны
![]()
Похожие работы
... . научн. картине мира, кот. дает естествознание. Необходимость применения естствено научных методов и законов в практической деят-ти гуманитарных специальностей и привело к постановке того курса, кот. мы будем изучать: Физика для гуманитариев. (38) Связь между разделами естествознания. Слово естествознание представляет из себя сочетание 2х слов: естество (природа) и знание. В настоящее время ...
... перед педагогическим сообществом ставится сегодня задача: как учесть вызовы времени и выстроить систему обучения таким образом, чтобы она максимально работала на учащихся. Поиск оптимальных путей решения делает проблему использования возможностей основного и дополнительного образования актуальной. Именно с этих позиций и были определены цели и задачи данной работы. 1. Теоретическая часть 1.1 ...
... философии - особенно с методологических позиций материалистического понимания истории и материалистической диалектики с учетом социокультурной обусловленности этого процесса. Однако в западной философии и методологии науки XX в. фактически - особенно в годы «триумфального шествия» логического позитивизма (а у него действительно были немалые успехи) - научное знание исследовалось без учета его ...
... Замечат. С.: Полемон, Герод Аттик, Аристид, Либаний. Ср. Schmid, "Der Atticismus in seinen Hauptvertretern" (1887-97). 17. Принцип детерминизма в философии. Индетерминизм. Детерминизм (от лат. determino - определяю), философское учение об объективной закономерной взаимосвязи и взаимообусловленности явлений материального и ...

0 комментариев