Навигация
7 груздей и 2 лисички,
У кого ответ готов?
Сколько было всех грибков?
Очень важное значение для активизации познавательной деятельности учеников на уроке имеют различные игры-соревнования, о которых мы уже писали выше.
Однако следует отметить тот момент, что младшие школьники быстро утомляются на уроках. Поэтому, с целью снятия мышечного напряжения используют различные физминутки. Однако они помогают решить и другие задачи: закрепление табличных случаев сложения, деления, умножения и вычитания.
Например:
Сколько раз ногою топнем? (8 - 4)
Сколько раз рукою хлопнем? (10: 2)
Мы присядем сколько раз? (3*2)
Мы наклонимся сейчас (9 + 2)
Мы подпрыгнем ровно столько (10 - 4)
Ай да счет! Игра и только!
2.5 Математические загадки
Немаловажное значение на уроках математики в начальных классах имеют загадки. Они расширяют кругозор детей, развивают любознательность и пытливость, тренируют внимание, память, мышление. Они могут быть использованы учителем во время внеклассной работы, на уроке, во время отдыха, так как интересны детям. Практика показывает, что применение загадок на уроках математики дают положительные результаты, так как они знакомят детей с окружающим миром, развивают логическое мышление.
Например:
У него четыре лапки,
Лапки цап-царапки.
Пара чутких ушек.
Он гроза для мышек.
(КОТ)
Говорит она беззвучно,
Но понятно и нескучно,
Ты беседуй чаще с ней,
Станешь в десять раз умней.
(КНИГА)
При знакомстве с цифрой 4 можно использовать загадку:
Вспушит она свои бока,
Свои четыре уголка,
И тебя, как ночь настанет,
Все равно к себе притянет.
(ПОДУШКА)
После того, как дети назвали отгадку, учитель просит их вспомнить, какое число прозвучало в загадке, объясняет, как изображается число 4, предлагает найти его в кассе цифр из счетного материала, назвать предыдущее и последующее числа. Особенно полезны загадки, по тексту которых надо догадаться, о какой цифре идет речь, и показать или написать ее. Такие загадки помогают запомнить графическое изображение цифр, учат узнавать их по описанию:
Я так мила, я так кругла,
Я состою из двух кружков.
Как рада я, что я нашла
Себе таких, как вы дружков.
(ВОСЕМЬ)
Вид ее - как запятая,
Хвост крючком, и не секрет
Любит всех она лентяев,
А лентяи ее - нет.
(ДВОЙКА)
Задачи, имеющие форму загадок, так же вызывают большой интерес, активность.
Например:
Отгадайте-ка, ребятки,
Что за цифра-акробатка?
Если на голову встанет,
Ровно на три больше станет.
(ШЕСТЬ)
Загадка - это логическое упражнение, при выполнении которого ребенок учится выделять существенные признаки предмета, а так же определять предмет по нескольким перечисленным признакам. Загадки могут быть различной степени сложности.
После того как дети отгадают загадку, можно предложить с помощью сигнальных блокнотов показать число, которое встретилось в загадке, определить, сколько в нем десятков и единиц каждого разряда, предыдущие и последующие числа.
Загадки могут использоваться при изучении темы "Меры времени":
Две сестрицы друг за другом.
Пробегают круг за кругом.
Коротышка - только раз,
Та, что выше - каждый час.
(СТРЕЛКИ ЧАСОВ)
На руке, и на стене,
И на башне в вышине
Ходят с боем и без боя.
Всем нужны - и нам с тобою.
(ЧАСЫ)
При знакомстве учащихся с календарем уместно использовать следующие загадки:
Годовой кусточек
Каждый день роняет листочек.
Год пройдет - весь куст опадет.
(КАЛЕНДАРЬ)
Выходило 12 молодцов,
Выносили 52 сокола,
Выпускали 365 лебедей.
(МЕСЯЦЫ, НЕДЕЛИ, ДНИ)
После отгадывания загадки задача учителя - добиваться обоснованного, доказательного ответа на вопрос: "Как ты догадался? Объясни!". Такая работа развивает логическое мышление, математическую речь, учит видеть в окружающем мире общие свойства и различия предметов и явлений.
2.6 Сказочные задачи
Среди занимательных задач особое место занимают сказочные задачи, т.е. задачи со сказочными образами, сказочными сюжетами. Казалось бы, сказка и математика - понятия не совместимые, однако сказочная форма позволяет ввести необычные, увлекательные ситуации в математические задачи. Именно такое соединение благоприятно для обучения, поскольку через сказочные элементы учитель может найти путь в сферу эмоций ребенка.
Встреча детей со знакомыми героями сказок не оставляет их равнодушными, сказка вызывает у детей радость, интерес. Известный математик А.И. Макрушевич отмечал, что человек, не воспитывающийся на сказках, труднее воспринимает мир идеальных стремлений, что благодаря сказке начинает отличать реальное от необычного, что нельзя развивать, минуя сказку, не только воображение, но и первые навыки критического мышления. Сказки в начальных классах нужны, особенно при изучении геометрического материала, который требует развитого воображения, умения обдумывать предложенную ситуацию, выявлять и использовать необходимую информацию для принятия решения.
На уроках, где имеет место сказка, всегда царит хорошее настроение, а это залог продуктивной работы. Сказка позволяет проникнуть на урок юмору. Фантазии, творчеству, а самое главное - учит детей быть добрыми и справедливыми. Желание помочь попавшему в беду герою, разобраться в сказочной ситуации - все это стимулирует умственную деятельность ребенка. Развивает его интерес к математике. В то же время встреча со сказочными героями в мире математики побуждает ребенка перечитать литературное произведение. Сказки и через задачи продолжают воспитывать детей. Сказки можно включать у уроки математики при повторении и закреплении изученной темы и использовать во внеклассных занятиях.
ПРИМЕР 1
Лиса Алиса и кот Базилио привели Буратино на пустырь - это Поле Чудес: если закопать золотые монеты, то на утро вырастет дерево, на котором в 3 раза больше золотых монет. Затем полученные монеты можно снова закопать в землю и снова вырастет дерево с монетами. Так можно снять несколько урожаев. Они предложили посторожить ночью монеты. В награду за услугу лиса и кот потребовали отдавать с каждого урожая 9 монет. Подумав немного, Буратино не согласился с их требованиями. Он заявил, что после двух урожаев у него совсем не останется денег. Уж лучше он сам посторожит. Сколько золотых монет было у Буратино?
Решение:
Второй урожай дает 9 монет, значит во второй раз Буратино посадит
9: 3=3 (монеты).
Первый урожай дал
3+9=12 (монет)
Значит, в первый раз Буратино посадил
12: 3=4 (монеты)
ПРИМЕР 2
Поросята Ниф-Ниф и Нуф-Нуф бежали от Волка к домику Наф-Нафа. Волку бежать до поросят (если бы они стояли на месте) 4 минуты. Поросятам бежать до домика6 минут. Волк бежит вдвое быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа?
Решение:
Волку бежать до домика Наф-Нафа 4 +6: 2=7 минут.6 минут меньше, чем 7 минут. Значит, поросята успеют добежать до домика Наф-Нафа.
2.7 Математические сказки.
Сказки любят все, но особенно - дети. Их можно включать в уроки математики при повторении или закреплении изученной темы и использовать во внеклассных занятиях. Именно для такой работы предназначены сказки "О нуле", "Победа знаний", "Герой планеты Фиалка". Для удобства сказка разбивается на части.
О нуле
Похожие работы
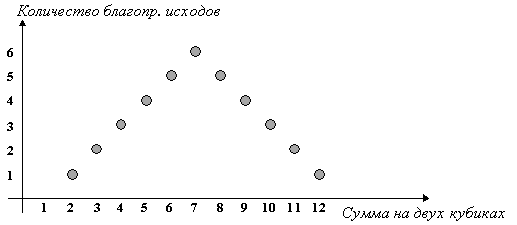
... монету второй раз не бросают), в четвертом — второму. Шансы игроков на выигрыш относятся как 3 к 1. В этом отношении и надо разделить ставку. Глава II. Элементы теории вероятностей и статистики на уроках математики в начальной школе (методика работы) Первый шаг на пути ознакомления младших школьников с миром вероятности состоит в длительном экспериментировании. Эксперимент повторяют много раз при ...
... задания и методические рекомендации по их использованию. Практическая значимость методических рекомендаций - в использовании их начинающими учителями школы первой ступени обучения для формирования учебно-исследовательской деятельности младших школьников. СПИСОК ЛИТЕРАТУРЫ 1. Антоненко, Т. Е. Приемы занимательности на уроках математики [Текст] / Т. Е. Антоненко // Начальная школа. 2008. №4 ...
... интересует. Соблюдение принципа наглядности – одно из основных требований, которому должно удовлетворять обучение математике в начальных классах. В начальных классах эффективно использовать технические средства обучения (ТСО) и наглядность по несколько минут на различных этапах урока. В процессе работы важно применять технические средства обучения в комплексе с другими средствами наглядности, ...
... передовых, творчески работающих преподавателей можно обнаружить множество других приемов, что требует их внимательного изучения и обобщения. Безусловно, важную роль в решении проблемы активизации мыслительной деятельности учащихся на занятиях играют внутренняя теплота, наличие у преподавателей глубокой убежденности в достоверности, точности тех положений, фактов, которые он излагает на лекции, ...

0 комментариев