Далеко-далеко, за морями и горами, Была страна Циферия. Жили в ней очень честные числа. Только Ноль отличался ленью и нечестностью

1. Далеко-далеко, за морями и горами, Была страна Циферия. Жили в ней очень честные числа. Только Ноль отличался ленью и нечестностью.

2. Однажды все узнали, что далеко за пустыней появилась королева Арифметика, зовущая к себе на службу жителей Циферии. Служить королеве захотели все.

Между Циферией и королевством Арифметики пролегала пустыня, которую пересекали четыре реки: Сложение, Вычитание, Умножение и Деление. Как добраться до Арифметики? Числа решили объединиться (ведь с товарищем легче преодолевать трудности) и попробовать перейти пустыню.

3. рано утром, как только солнце косыми лучами коснулось земли, числа двинулись в путь. Долго шли они под палящим солнцем и наконец добрались до реки Сложение. Числа бросились к реке напиться, но река сказала: "Станьте парами и сложитесь, тогда дам вам напиться". Все исполнили приказание реки. Исполнил желание и лентяй Ноль, но число, с которым он сложился, осталось недовольно: ведь воды давала река столько, сколько единиц было в сумме, а сумма не отличалась от числа.

4. Солнце еще больше печет.д.ошли до реки Вычитание. Она тоже потребовала за воду плату: стать парами и вычесть меньшее число из большего; у кого ответ получится меньше тот получит больше воды. И снова число, стоящее с нолем, оказалось в проигрыше и было расстроено.

5. Побрели числа дальше по знойной пустыне. Река Умножение потребовала от чисел перемножиться. Число, стоящее в паре с Нолем, вообще не получило воды. Оно еле добрело до реки Деление.

6. А у реки Деление никто из чисел не захотел становиться в пару с нолем. С тех пор ни одно число не делится на Ноль.

7. Правда, королева Арифметика примирила все числа с этим лентяем: она стала подставлять к числу Ноль, и число от этого увеличивалось в десять раз. И стали числа жить-поживать и добра наживать.

Работать со сказкой можно по-разному: после чтения задать ряд вопросов; попросить детей на отдельных этапах продолжить сказку; рассмотреть сказку как задание с пропусками.

Приведем некоторые примерные вопросы, которые можно задать учащимся. Порядковый номер соответствует абзацу сказки.

Почему страна называлась Циферией? Что означает число ноль?

Чем занимается королева Арифметика в математике? (Изучает числа и действия над ними) Какие реки разделяли страну Циферию и королевство А рифметики? Какое общее название можно дать этим рекам? (Действия) Кто собирался переходить через пустыню? (Числа) Чем числа отличаются от цифр?

Почему число, с которым сложился ноль, осталось недовольно?

Приведите два примера, иллюстрирующих слова сказки: "…стать парами и вычесть меньшее число из большего: у кого ответ получился меньше, тот получит больше воды. ". почему число, стоящее в паре с нулем, оказалось в проигрыше? Могут ли числа встать так, чтобы каждой паре досталось воды поровну? Приведите примеры.

Почему число, стоящее в паре с Нулем, не получило воды от реки Умножение?

Почему при переходе через реку Деление числа не захотели становиться в пару с Нолем?

Во сколько раз первое число больше или меньше второго: 7 и 70, 3 и 30, 50 и 5?

Предложить ребятам сочинить продолжение сказки можно, видимо, после четвертого пункта. Здесь уже чувствуется авторский замысел, математическая закономерность. Впрочем, такую работу можно организовать и после третьего пункта, если дать некоторые советы: а) каждая река ставит перед числами задачу, которую невозможно успешно решать в паре с Нолем; б) сказка должна закончиться счастливо, как это обычно бывает.

Под заданием с пропусками подразумевается Выделение интонацией (отдельные предложения можно выписать на доске) отсутствие некоторых слов, но которые можно восстановить по смыслу сказки, на основе строгой взаимосвязи математических понятий. Например, в 5-м абзаце: "Число, стоящее в паре с Нолем, вообще не… воды"; в 6-м: " Она стала просто приписывать ноль рядом с числом, которое от этого... в…раз".

Вышеописанные приемы работы можно комбинировать. Такие сказки на уроках повторения и закрепления делают их более разнообразными и интересными. Сказки и вопросы к ним дают большой воспитательный эффект и способствуют развитию мышления.

Вот еще несколько сказок, с которыми можно провести аналогичную работу.

Победа знаний.

Это было давно.

В некотором царстве, в некотором государстве на престол взошел неграмотный король, в детстве он не любил математику, родной язык, рисование, пение, чтение и труд. Вырос этот король неучем. Стыдно перед народом. И решил король: пусть все в этом государстве будут неграмотными. Он закрыл все школы, но разрешил изучать только военное дело, чтобы завоевать побольше земель и стать богатым.

Вскоре армия этого государства стала большой и сильной. Она беспокоила все близлежащие страны, особенно доставалось маленьким.

Короля-неуча звали Пуд. Он стал предводителем своей разбойничьей армии.

По соседству со страной неучей находилась страна Длина. Ее король был умным и образованным человеком: знал арифметику, различные языки; кроме того, великолепно владел военным делом.

Армия в этой стране была небольшая, но хорошо обученная. Славилась она своей разведкой и бегунами на длинные дистанции.

Король Пуд подошел со своими войсками к государству Длина и разбил лагерь около границы. Как спасти государство? Его король, зная, что Пуд и его подчиненные не умеют считать и не знают, что значат слова кило (тысяча), санти (сто), деци (десять), решил провести военную операцию.

Через два дня перед лагерем войск Пуда появилась на повозке большая фанерная кукла. Часовые ее не хотели пропускать, но кукла сказала, Что она - подарок. От государства Длина королю Пуду. Часовые вынуждены были пропустить куклу.

Повозка с куклой въехала в лагерь. Пуд с приближенными рассмотрели куклу и удивились ее размерам и умению говорить по-человечески.

Кукла сказала, что ее зовут Кило и что у нее есть младшие братья Метр и Дециметр.

Солнце все ниже и ниже. На землю опустилась ночь. Когда весь лагерь Пуда заснул, кукла раскрылась, и из нее вышли 1000 кукол по имени Метр, а из каждой из них - 10 кукол, которых звали Дециметр, из каждого Дециметра - по 10 воинов-Сантиметров. Они окружили спящее войско и уничтожили его. Только король Пуд спасся бегством (позже его найдут в другом королевстве).

Так умный король победил неуча - короля Пуда. И все соседние государства стали жить в мире и дружбе.

Герой планеты "Фиалка"

Сегодня на всей земле шумел праздник. Впервые в истории человек отправлялся к планете "Фиалка", на которой жили разумные существа.

Прошло полчаса полета. И вдруг из машинного отделения послышался шум, не предусмотренный инструкциями. К счастью, аварии не было. На корабле оказался мальчик Коля. Что делать? Космонавты решили сообщить о происшедшем в центр управления полетом и продолжать экспедицию.

Наконец экипаж достиг неизвестной планеты. В нескольких километрах от места приземления расположился удивительный город: все дома в нем были шарообразной формы. Жители Фиалки не умели вычислять площадь прямоугольника. Земляне решили помочь им, а заодно проверить, на что способен их безбилетный пассажир.

Коля испугался: математику он не любил, домашние задания всегда списывал у товарищей. Но выхода не было. С трудом он вспомнил, что квадратик со стороной 1 см имеет площадь 1 кв. см, 1 м - 1 кв. м и т.д. Как же найти площадь прямоугольника? Коля нарисовал прямоугольник, в котором уместилось 12 маленьких квадратиков. Вдоль большей 4 квадратика, а вдоль меньшей 3. Затем Коля изобразил еще один прямоугольник. В нем поместилось 30 квадратиков, длина прямоугольника равнялась 10 квадратикам, а ширина 3.

Что же делать? - думал Коля - Стороны прямоугольника равны 4 и 3 квадрата, а площадь 12, стороны прямоугольника равны 10 и 3 квадратикам, а площадь 30. Знаю! - закричал мальчик. - Чтобы узнать площадь прямоугольника, надо длину умножить на ширину.

Коля доложил командиру корабля о выполнении задания.

Эту сказку можно использовать не только при закреплении, но и при изучении нового материала - площади прямоугольника. Ученик может выступать а роли Коли, сделать небольшое, но открытие. Элементы проблемного обучения в форме игры-сказки вызывают у детей большой интерес.

 

2.8 Задачи занимательного характера

 

В привитии детям интереса к урокам математики большую роль играют задачи занимательного характера. Такие задачи, как показывает практика, вносят в урок оживление, повышают интерес к знаниям, развивают воображение и память детей. Дети решают задачи такого вида с большим удовольствием.

1) Зайцы по лесу бежали,

Волчьи следы по дороге считали.

Стая большая волков здесь прошла.

Каждая лапа в снегу их видна.

Оставили волки 120 следов.

Сколько, скажите, здесь было волков?

2) На птичьем дворе гусей дети кормили,

Целыми семьями их выводили.

Всего было 5 гусиных семей,

В каждой семье по 12 детей.

Папа и мама, бабушка с дедом.

Сколько гусей собралось за обедом?

При решении задач такого типа учитель может задавать детям следующие вопросы:

Читал ли ты сказку, по отрывку из которой составлена задача?

Какой рисунок к этой задаче ты бы нарисовал?

Эти задачи способствуют развитию интереса к математике, углублению и расширению математических знаний, осознанию силы и практической значимости математики. Одна из важнейших задач начального обучения - развитие у детей логического мышления. Такое мышление проявляется в том, что при решении задач ребенок соотносит суждения о предметах, отвлекаясь от особенностей их наглядных образов, рассуждает, делает выводы. Умение мыслить логически, выполнять умозаключения без наглядной опоры, сопоставлять суждения нужны для изучения учебного материала не только в начальных классах, но и в средних и старших

2.9 Головоломки

 

Большое значение в начальных классах имеют головоломки, именно они закладывают основы доказательного мышления.

Например:

1) Пятью прямыми линиями разделите циферблат так, чтобы в каждой части числа при сложении давали бы равную сумму.

2) Какие цифры скрыты? Подумайте и догадайтесь:

*** - **=1

Близки к головоломкам и задачи на сообразительность.

Например:

Лестница состоит из 15 ступеней.

На какую лестницу нужно встать, чтобы быть на середине лестницы? (На восьмую).

2) Валя и Миша весят столько же, сколько Боря и Володя. Миша весит 32 кг, Боря 40 кг.

Кто тяжелее: Валя или Володя? (Валя).

3) Груша дороже яблока в 2 раза. Что дороже: 8 яблок или 4 груши?

(8 яблок и 4 груши стоят одинаково).

Один из наиболее распространенных видов головоломок - магические квадраты:

В шестнадцати клетках квадрата расставьте числа.0,1,2…14,15 так, чтобы сумма чисел по горизонтали, вертикали и диагонали была равна 30.

0	14	13	3
11	5	6	8
7	9	10	4
12	2	1	15

2) В двадцати пяти клетках квадрата расставьте числа 1,1,1,1,12,2,2,2,2,3,3,3,3,3,5,5,5,5,5, так, чтобы по горизонтали, вертикали и двум диагоналям сумма была равна 15.

1	4	2	5	3
4	2	5	3	1
2	5	3	1	4
5	3	1	4	2
3	1	4	2	5

Разновидностью магических квадратов являются магические треугольники:

Данный треугольник составлен из 9 маленьких треугольников, в которые вписаны числа.

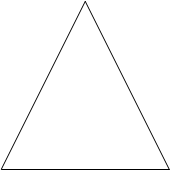 - Найдите суммы чисел в треугольниках, составленных из 4 маленьких треугольников.

3

7

6 4

8 9

 1 5 2

Ответ:

1+5+6+8=20

2+4+5+9=20

Мы видит, что сумма чисел в каждом треугольнике, который образован четырьмя маленькими треугольниками, представляет собой одно и тоже числа. Такие треугольники называются магическими. Магический ли этот треугольник?

 

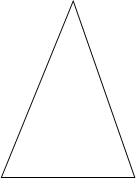3

7

4 6

9 8

2 5 1

Задания на смекалку и на сообразительность следует предлагать для самостоятельной работы, и только при затруднении большинства учащихся учитель анализирует со всем классом во внеурочное время.

1.

 на (витрина) Д»40» га (дорога)