Навигация
3.1.2 Спектр видеосигнала
Спектральную плотность видеосигнала находим с помощью прямого преобразования Фурье математической модели видеосигнала (3.2):
![]() , (3.3)
, (3.3)
где L – оператор Фурье;
F(jw) – спектральная плотность видеосигнала, В;
![]() - циклическая частота,
- циклическая частота, ![]() ;
;
j – мнимая единица.
Имеем:
![]() , (3.4)
, (3.4)
Используя подстановку ![]() , где f – частота Гц, преобразуем выражение (3.4) и перейдем к частоте в герцах.
, где f – частота Гц, преобразуем выражение (3.4) и перейдем к частоте в герцах.
 (3.5)
(3.5)
Данные положения иллюстрируются графиком спектральной плотности видеосигнала рисунок 3.2.
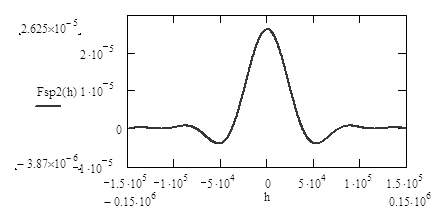
Рисунок 3.2 - Спектральная плотность видеосигнала
3.2 Периодическая последовательность видеосигналов
3.2.1 Математическая модель периодической последовательности видеосигналов
Математическую модель периодической последовательности видеосигналов fT(t) можно представить в следующем виде:
![]() , (3.6)
, (3.6)
где
n – переменная суммирования, целое число.
Графическое изображение периодической последовательности видеоимпульсов приведено на рисунок 3.3.

Рисунок 3.3 - Периодическая последовательность видеосигналов.
3.2.2 Спектр периодической последовательности видеосигналов
Периодический сигнал может быть представлен рядом Фурье:
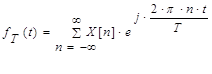 , (3.7)
, (3.7)
где X[n] – коэффициенты ряда Фурье.
 (3.8)
(3.8)
Согласно выражениям (3.8) и (3.9) периодический сигнал состоит из суммы бесконечного числа гармонических колебаний кратных частот (гармоник), вклад которых в общую сумму определяется весовыми коэффициентами X[n]. Таким образом, являясь амплитудами дискретных частотных компонентов (гармоник) составляющих данный сигнал, коэффициенты X[n] образуют дискретный спектр периодического сигнала рисунок 3.4. «Востановленный» с помощью ряда Фурье сигнал, при суммировании десяти первых гармоник, приведен на рис 3.5.
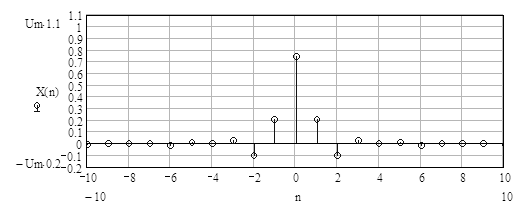
Рисунок 3.4 - Спектр периодического сигнала.
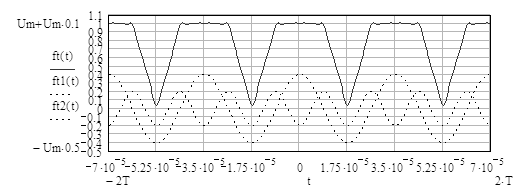
Рисунок 3.5 - Сигнал представленный рядом Фурье, первая и вторая гармоники (пунктирные линии).
3.3 Радиосигнал
3.3.1 Математическая модель радиосигнала
Радиосигнал с огибающей в форме видеосигнала находим из соотношения:
![]() , (3.9)
, (3.9)
где
![]() - математическая модель радиосигнала, В;
- математическая модель радиосигнала, В;
f0 - частота несущего высокочастотного колебания, Гц;
![]() - начальная фаза колебания, рад.
- начальная фаза колебания, рад.
Найдем частоту несущего высокочастотного колебания f0, которая совпадает с резонансной частотой колебательного звена:
![]() (3.10)
(3.10)
где
![]() - индуктивность колебательного звена, Гн,
- индуктивность колебательного звена, Гн,
![]() - значение емкости колебательного звена, Ф.
- значение емкости колебательного звена, Ф.
Подставляя численное значение частоты несущего высокочастотного колебания (f0=918,9 кГц), в (3.9) построим график радиосигнала рисунок 3.6.

Рисунок 3.6 - Радиосигнал
3.3.2 Спектр радиосигнала
Для отыскания спектральной плотности радиосигнала воспользуемся соотношением:
![]() , (3.11)
, (3.11)
где
![]() - спектральная плотность видеосигнала (3.5) на соответствующих частотах, В;
- спектральная плотность видеосигнала (3.5) на соответствующих частотах, В;
Таким образом, подставляя в выражение (3.11) аналитическое выражение для спектральной плотности видеосигнала (3.5) , и принимаем ![]() .
.
Графическое изображение спектральной плотности радиосигнала приведено на рисунок 3.7. Как видно, при достаточно большом значении частоты несущего высокочастотного колебания, спектральная плотность радиосигнала представляет собой две симметричные копии спектра видеосигнала с половинной амплитудой перенесенные на частоту несущего колебания.
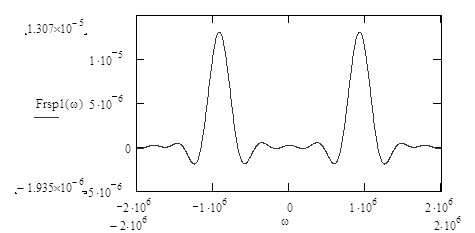
Рисунок 3.7 - Спектральная плотность радиосигнала
Похожие работы
... входом и выходом. Такой факт позволяет использовать дифференциальную схему на высоких частотах, не применяя схему нейтрализации этой паразитной связи. Данная микросхема предназначена для использования в приемниках амплитудно-модулированных сигналов. Она может работать в диапазоне частот до 30 МГц, имея при этом усиление, позволяющие принимать сигналы с отношением сигнал–шум на выходе 20 dВ, при ...
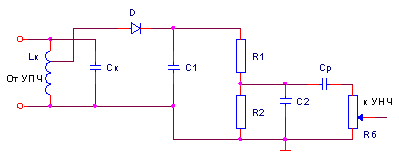
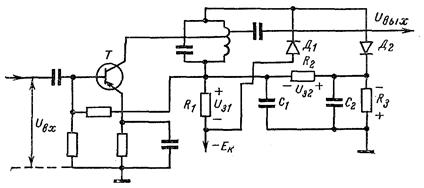
... получить ограничитель мгновенных значений. В зависимости от вида нелинейной цепи АО подразделяются на диодные и транзисторные. Рисунок 1.2 – Структурная схема амплитудного ограничителя 1.2 Диодные амплитудные ограничители Простейшим ограничителем амплитуды является диодный [1]. Для его осуществления параллельно нагрузочному колебательному контуру последнего каскада усилителя напряжения ...
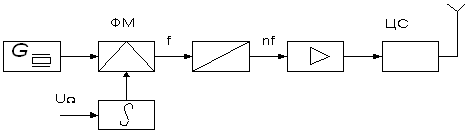
... , обеспечивающий ослабление высших гармоник на 40 дБ вне рабочего диапазона частот передатчика в соответствии с техническим заданием (см. раздел 4 АСЧЁТ ВЫХОДНОГО ФИЛЬТРА). Поскольку в данной курсовой работе необходимо спроектировать только оконечный мощный каскад связного передатчика с ЧМ, то для конкретизации, входящие в его состав блоки обведены синей пунктирной линией, и именно о них далее ...
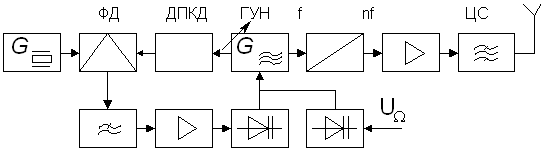
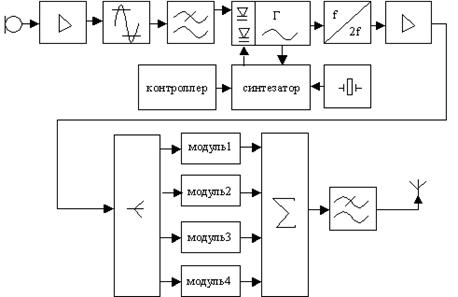
а цифровых ИС можно реализовать практически любой алгоритм обработки сигнала, осуществляемый в приемно-усилительных устройствах, включая элементы оптимального радиоприема. Связные РПУ с частотной модуляцией проектируются для работы на одной фиксированной частоте или в диапазоне частот. В первом случае рабочая частота стабилизируется кварцевым резонатором, а для генерации ЧМ колебаний могут быть ...



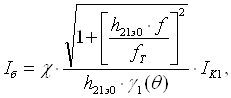
0 комментариев