Навигация
Аналитический сигнал, соответствующий радиосигналу
3.4 Аналитический сигнал, соответствующий радиосигналу
Аналитический сигнал, соответствующий реальному физическому сигналу ![]() , определяется соотношением:
, определяется соотношением:
![]() , (3.12)
, (3.12)
где
![]() - функция, сопряженная по Гильберту выходному сигналу;
- функция, сопряженная по Гильберту выходному сигналу;
![]() - реальный физический сигнал.
- реальный физический сигнал.
![]() . (3.13)
. (3.13)
Также аналитический сигнал может быть представлен через модуль аналитического сигнала ![]()
![]() , (3.14)
, (3.14)
и полную фазу ![]()
![]() (3.15)
(3.15)
в виде ![]() (3.16)
(3.16)
Для радиосигнала полную фазу можно записать в форме:
![]() , (3.17)
, (3.17)
где w0 - частота несущего высокочастотного колебания, ![]() ;
;
Q(t) - изменяющаяся во времени фаза, рад; Q0 - постоянная во времени начальная фаза, рад. В этом случае аналитический сигнал ![]() определяется соотношением:
определяется соотношением:
![]() ,
(3.18)
,
(3.18)
где
![]() -комплексная огибающая аналитического сигнала, соответствующего радиосигналу, В;
-комплексная огибающая аналитического сигнала, соответствующего радиосигналу, В;
Заметим, что комплексная огибающая аналитического сигнала вещественна, то есть не имеет мнимой составляющей и представляет собой видеосигнал (3.2). Поэтому аналитический сигнал, соответствующий радиосигналу можно представить:
![]()
Спектральная плотность ![]() аналитического сигнала сосредоточена только в области положительных частот и находится из соотношения:
аналитического сигнала сосредоточена только в области положительных частот и находится из соотношения:
 , (3.19)
, (3.19)
где
![]() - спектральная плотность радиосигнала (3.11)
- спектральная плотность радиосигнала (3.11)
Построим график спектральной плотности аналитического сигнала рисунок 3.8.
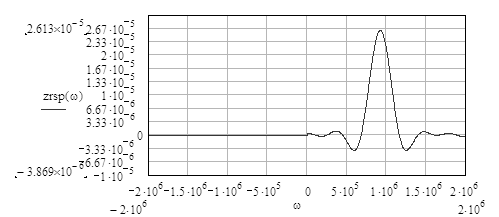
Рисунок 3.8 - Спектральная плотность аналитического сигнала
3.5 Дискретный сигнал, соответствующий видеосигналу
В соответствии с теоремой Парсеваля полная энергия сигнала равна:
 , (3.20)
, (3.20)
Ограничим спектр исходного видеосигнала некоторой граничной частотой fg, таким образом, что бы энергия сигнала, с «ограниченным спектром» была равна 99% энергии исходного сигнала. Находим граничную частоту по формуле, из условия:
 , (3.21)
, (3.21)
Получаем fg»63,2 кГц.
Если теперь считать, что сигнал имеет спектр, наивысшая частота которого равна fg, то в соответствии с теоремой Котельникова, сигнал может быть полностью определен дискретными выборками, взятыми с частотой 2fg, называемой частотой дискретизации.
Найдем интервал дискретизации Td:
![]() , (3.22)
, (3.22)
Математическую модель дискретного fd(n) сигнала можно записать в следующем виде:
![]() , (3.23)
, (3.23)
где
n,k – целые числа;
f(kTd) – выборки из видеосигнала (3.2) кратные интервалу дискретизации;
d(n) – единичный импульс определенный как:
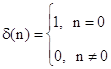 , (3.24)
, (3.24)
Графическое изображение дискретного сигнала fd(n) приведено на рисунок 3.9.
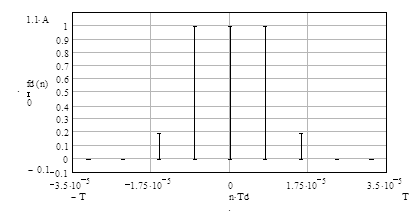
Рисунок 3.9 - Дискретный сигнал
Для отыскания спектральной плотности дискретного сигнала воспользуемся соотношением:
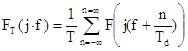 , (3.25)
, (3.25)
где 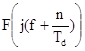 - спектральная плотность видеосигнала (3.5) на соответствующих частотах.
- спектральная плотность видеосигнала (3.5) на соответствующих частотах.
Модуль спектральной плотности дискретного сигнала приведен на рисунок 3.10.

Рисунок 3.10 - Модуль спектральной плотности дискретного сигнала, модуль спектральной плотности видеосигнала.
Таким образом, спектр дискретного сигнала периодичен по частоте, с периодом равным частоте дискретизации. Если эффект наложения спектров отсутствует, то в полосе частот от минус половина частоты дискретизации до плюс половина частоты дискретизации, спектр дискретного сигнала равен спектру аналогового сигнала. Для случая приведенного на рисунок 3.11 это условие не выполняется. Поэтому восстановленный сигнал будет искажен рисунок 3.11.
Похожие работы
... входом и выходом. Такой факт позволяет использовать дифференциальную схему на высоких частотах, не применяя схему нейтрализации этой паразитной связи. Данная микросхема предназначена для использования в приемниках амплитудно-модулированных сигналов. Она может работать в диапазоне частот до 30 МГц, имея при этом усиление, позволяющие принимать сигналы с отношением сигнал–шум на выходе 20 dВ, при ...
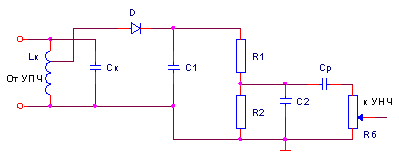
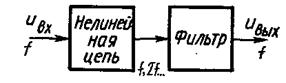
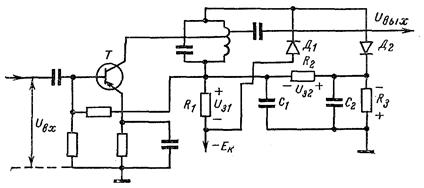
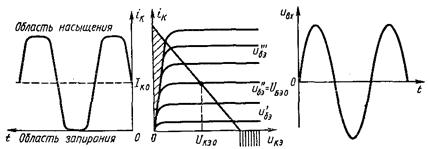
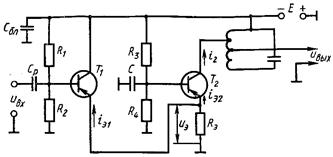
... получить ограничитель мгновенных значений. В зависимости от вида нелинейной цепи АО подразделяются на диодные и транзисторные. Рисунок 1.2 – Структурная схема амплитудного ограничителя 1.2 Диодные амплитудные ограничители Простейшим ограничителем амплитуды является диодный [1]. Для его осуществления параллельно нагрузочному колебательному контуру последнего каскада усилителя напряжения ...
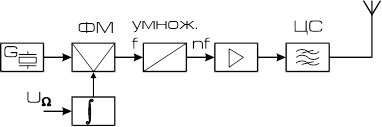
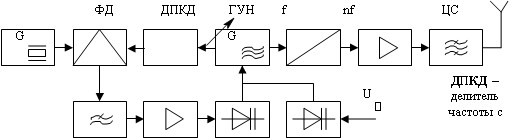
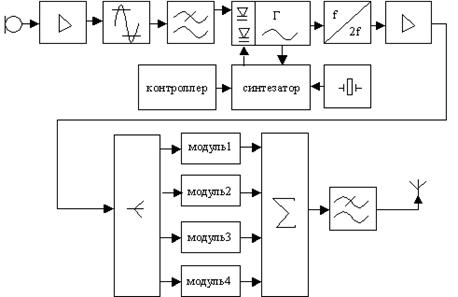
... , обеспечивающий ослабление высших гармоник на 40 дБ вне рабочего диапазона частот передатчика в соответствии с техническим заданием (см. раздел 4 АСЧЁТ ВЫХОДНОГО ФИЛЬТРА). Поскольку в данной курсовой работе необходимо спроектировать только оконечный мощный каскад связного передатчика с ЧМ, то для конкретизации, входящие в его состав блоки обведены синей пунктирной линией, и именно о них далее ...
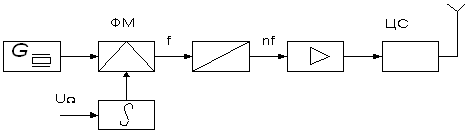
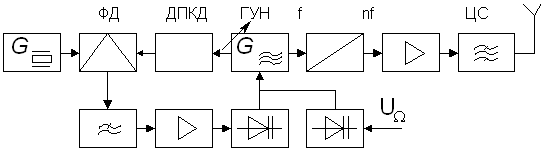
а цифровых ИС можно реализовать практически любой алгоритм обработки сигнала, осуществляемый в приемно-усилительных устройствах, включая элементы оптимального радиоприема. Связные РПУ с частотной модуляцией проектируются для работы на одной фиксированной частоте или в диапазоне частот. В первом случае рабочая частота стабилизируется кварцевым резонатором, а для генерации ЧМ колебаний могут быть ...



0 комментариев