Навигация
Сигнал представленный рядом Котельникова
3.6 Сигнал представленный рядом Котельникова
Получить сигнал, определенный в любой момент времени (аналоговый сигнал fa(t)) можно используя интерполяционную формулу:
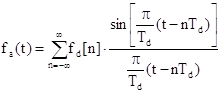 , (3.26)
, (3.26)
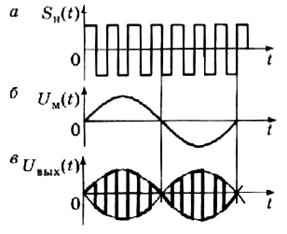
Данный ряд называется рядом Котельникова и позволяет полностью восстановить аналоговый сигнал fa(t) из дискретных выборок этого сигнала, если сигнал fa(t) имеет ограниченный спектр с максимальной частотой fg, и если выборки взяты с частотой не меньшей 2fg. Поскольку сигнал, подвергнутый дискретизации (3.2), имеет неограниченный спектр (3.5), то восстановление сигнала (3.26) по его выборкам (3.23), будет неточным. Уменьшить ошибку до любого уровня можно увеличивая частоту дискретизации. Сигнал восстановленный с помощью выражения (3.26), приведен на рисунок 3.11.
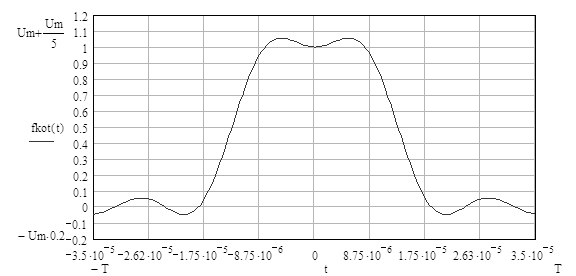
Рисунок 3.11 - Сигнал представленный рядом Котельникова.
3.7 Выводы
Анализируя формулы и графики, приведенные в разделе 3 можно сделать несколько выводов:
1) Ширина спектра зависит от длительности импульса: чем короче сигнал, тем шире спектр и наоборот.
2) Огибающая спектра периодического сигнала имеет форму спектральной плотности одиночного сигнала.
3) Спектр амплитудно-модулированного радиосигнала представляет собой фактически спектр модулирующего видеосигнала, смещенный по оси частот на (f0)ω0.
4) Спектр дискретного сигнала представляет собой сумму спектров видеосигнала смещенных друг относительно друга на n×2×fg.
4 Анализ электрических цепей
4.1 Исследование апериодического звена
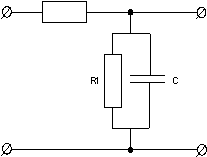
Рисунок 4.1 – Электрическая принципиальная схема апериодического звена.
R1=1000 Ом
C=0.5 мкФ
![]()
4.1.1 Комплексный частотный коэффициент передачи апериодического звена
Найдем математическое выражение для комплексного частотного коэффициента передачи, исходя из схемы приведенной на рисунке 4.1:
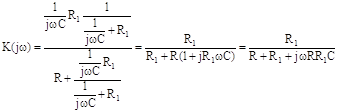 (4.1)
(4.1)
Из формулы (4.1) легко получить АЧХ и ФЧХ апериодического звена.
АЧХ можно получить, взяв модуль комплексного частотного коэффициента передачи.
ФЧХ вычислим по формуле (4.2).
![]() (4.2)
(4.2)
Построим графики АХЧ и ФЧХ:

Рисунок 4.2– АЧХ апериодического звена

Рисунок 4.3– ФЧХ апериодического звена
4.1.2 Операторный коэффициент передачи
Запишем операторный коэффициент передачи для апериодического звена
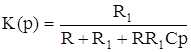 . (4.3)
. (4.3)
4.1.3 Импульсная характеристика апериодического звена
Импульсная характеристика цепи определяется как реакция цепи на входной сигнал в виде дельта-функции.
Импульсная характеристика находится ОПЛ от операторного коэффициента передачи. ОПЛ определяется следующим образом:
 . (4.4)
. (4.4)
Однако на практике при расчетах операторным методом пользуются таблицами прямых и обратных преобразований Лапласа. Это в значительной мере облегчает вычисления. Вычислив обратное преобразование Лапласа от операторного коэффициента передачи его получим:
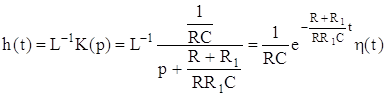 . (4.5)
. (4.5)
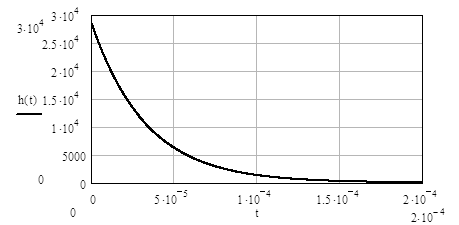
Рисунок 4.4– Импульсная характеристика апериодического звена
4.1.4 Переходная характеристика апериодического звена
Переходная характеристика цепи представляет собой реакцию цепи на сигнал в виде функции Хевисайда. В общем случае переходная характеристика находится как:
![]() , (4.6)
, (4.6)
где L-1 – обратное преобразование Лапласа.
Вычислив выражение (4.6) получим:
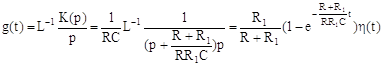 . (4.7)
. (4.7)
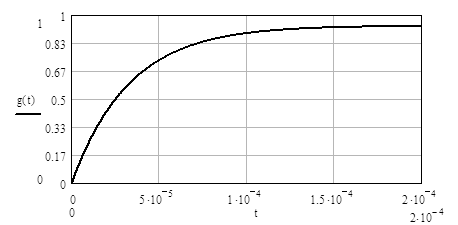
Рисунок 4.5– Переходная характеристика апериодического звена
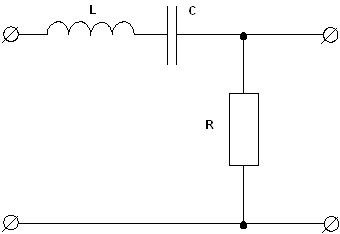
4.2 Исследование колебательного звена
|

Рисунок 4.6 - Схема электрическая принципиальная колебательного звена
L=1.5 мкГн
С=20.000 пФ
Q=50
Для последовательного колебательного контура справедлива формула:
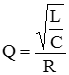 ,
,
Выразив R получим и подставив численные значения Q, L и C найдем R=0,173 Ом.
4.2.1 Комплексный частотный коэффициент передачи колебательного звенаНайдем математическое выражение для комплексного частотного коэффициента передачи, исходя из схемы приведенной на рисунке 4.6:
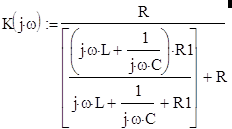 . (4.8)
. (4.8)
Из формулы (4.8), как и для апериодического звена, можно легко получить АЧХ и ФЧХ колебательного звена.
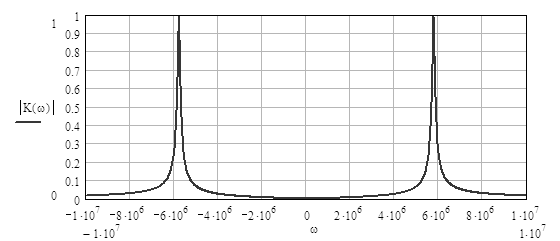
Рисунок 4.7 – АЧХ колебательного звена
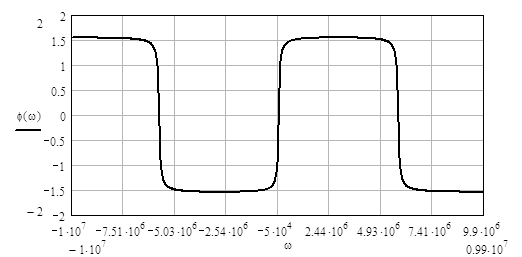
Рисунок 4.8 – ФЧХ колебательного звена
4.2.2 Операторный коэффициент передачиЗапишем операторный коэффициент передачи для колебательного звена:
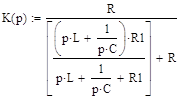 (4.9)
(4.9)
Похожие работы
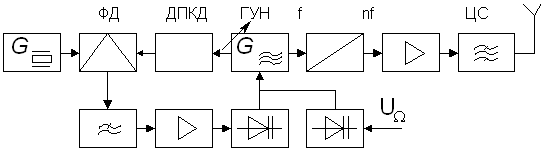
... входом и выходом. Такой факт позволяет использовать дифференциальную схему на высоких частотах, не применяя схему нейтрализации этой паразитной связи. Данная микросхема предназначена для использования в приемниках амплитудно-модулированных сигналов. Она может работать в диапазоне частот до 30 МГц, имея при этом усиление, позволяющие принимать сигналы с отношением сигнал–шум на выходе 20 dВ, при ...
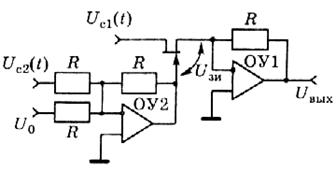
... получить ограничитель мгновенных значений. В зависимости от вида нелинейной цепи АО подразделяются на диодные и транзисторные. Рисунок 1.2 – Структурная схема амплитудного ограничителя 1.2 Диодные амплитудные ограничители Простейшим ограничителем амплитуды является диодный [1]. Для его осуществления параллельно нагрузочному колебательному контуру последнего каскада усилителя напряжения ...
... , обеспечивающий ослабление высших гармоник на 40 дБ вне рабочего диапазона частот передатчика в соответствии с техническим заданием (см. раздел 4 АСЧЁТ ВЫХОДНОГО ФИЛЬТРА). Поскольку в данной курсовой работе необходимо спроектировать только оконечный мощный каскад связного передатчика с ЧМ, то для конкретизации, входящие в его состав блоки обведены синей пунктирной линией, и именно о них далее ...
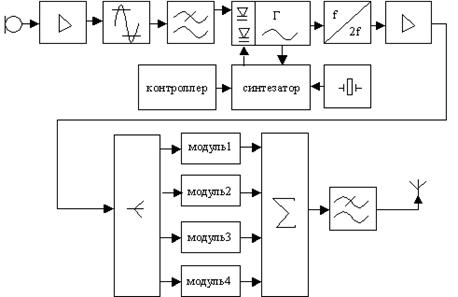
а цифровых ИС можно реализовать практически любой алгоритм обработки сигнала, осуществляемый в приемно-усилительных устройствах, включая элементы оптимального радиоприема. Связные РПУ с частотной модуляцией проектируются для работы на одной фиксированной частоте или в диапазоне частот. В первом случае рабочая частота стабилизируется кварцевым резонатором, а для генерации ЧМ колебаний могут быть ...



0 комментариев