Навигация
Нахождение комплексной функции передачи
2. Нахождение комплексной функции передачи
Для нахождения комплексной функции передачи воспользуемся методом обобщенных чисел.
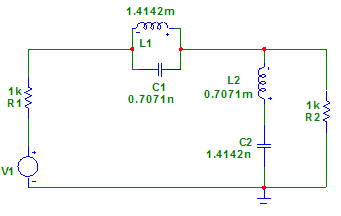
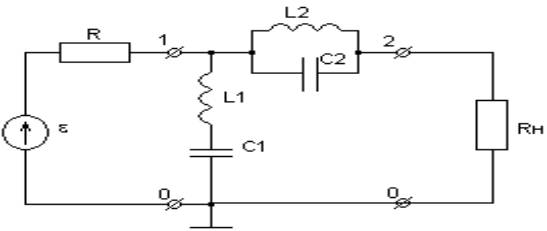
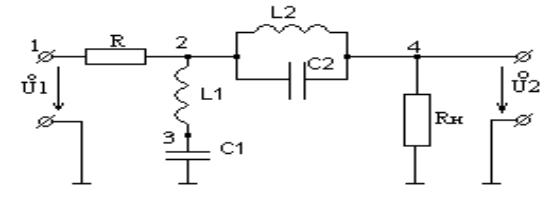
Рис 2. Схема фильтра для вычисления комплексной функции передачи.
Составим проводимости узлов:
0: Y=![]() 2: Y=
2: Y=![]()
1: Y=![]() 3: Y=
3: Y=![]()
Мы дополнительно ввели один узел между элементами L2 и C2.
Диагональная матрица собственных проводимостей узлов
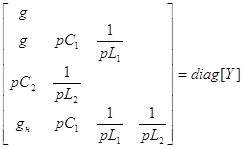
Помножим все элементы на p и заменим ![]() ;
;
![]() ;
; ![]() ;
; ![]()
Получаем звездное число:
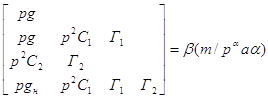
Напишем обобщенное число:
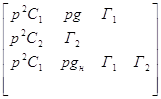 =
=![]()
Далее определяем древесное число:
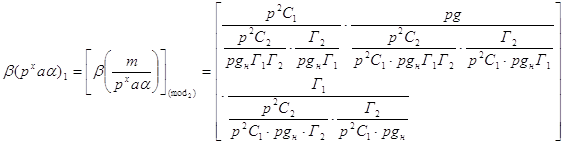
Определитель:
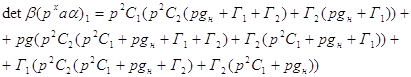
Числитель функции передачи:
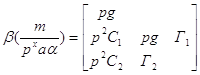
Древесное число числителя:
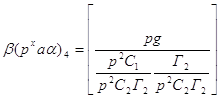
Формула для вычисления функции передачи:
H41(p)=![]()
Числитель:
![]()
Подставим все значения в формулу и поделим на p:
H41(p)=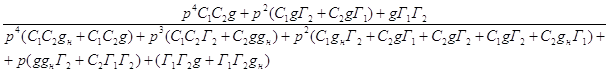
![]()
Преобразуем обратно Г1 =1/L1 и Г2 =1/L2
Подставим все значения элементов в формулу H41(p),получаем:
![]()
Перейдем к нормированной частоте:
![]()
Для проверки и для того, чтобы удостовериться, что расчеты методом обобщенных чисел верны, воспользуемся результатом, полученным при использовании программы General Numbers.vi
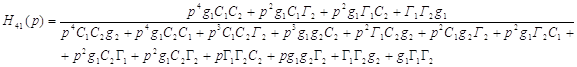
где ![]() .
.
Как мы видим, функция передачи, полученная методом обобщенных чисел, полностью совпадает с функцией передачи, рассчитанной с помощью программы General Numbers.vi.
3. Карта полюсов и нулей
По ранее найденной комплексной функции передачи цепи определим полюса и нули:
![]()
Для нахождения нулей выпишем отдельно числитель функции и приравняем его к нулю. Корни данного уравнения и будут являться нулями.
![]() =0
=0
Решая данное уравнение, получим:
p1,2,3,4=![]()
Для нахождения полюсов выпишем отдельно знаменатель функции и приравняем его к нулю. Корни данного полинома и будут являться полюсами.
![]()
Решив данное уравнение, мы получили полюса:
p1,2=-0.4775![]() 1.3610j
1.3610j
p3,4=-0.2296![]() 0.6542j
0.6542j
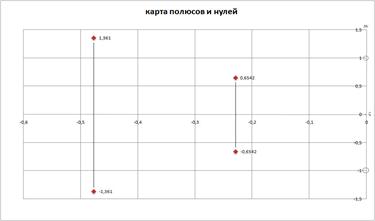
Рис 3. Карта полюсов и нулей.
По полученным значениям построим карту полюсов и нулей:
По виду карты полюсов и нулей можно определить некоторые особенности цепи:
1. Цепь является минимально-фазовой, т.к. в правой полуплоскости отсутствуют нули.
2. Цепь является устойчивой, т.к. в правой полуплоскости нет полюсов.
4. Нахождение функций АЧХ, ФЧХ и ЛАЧХ. Графики функций.
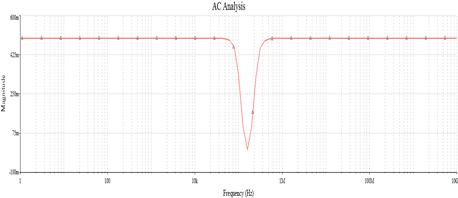
Рис 4. Амплитудно-частотная характеристика.
Графики АЧХ, ФЧХ и ЛАЧХ построим с помощью программ MultiSim 10 и Micro Cap 9. Амплитудно-частотная характеристика (АЧХ) определяется как:
![]() =
=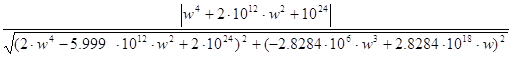
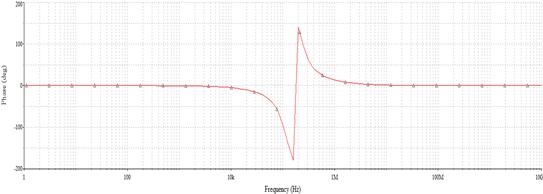
Рис 5. Фазо-частотная характеристика.
Фазо-частотная характеристика (ФЧХ) определяется как: ![]()
По ФЧХ определяем время задержки сигнала:
![]() мкс.
мкс.
Логарифмическая АЧХ определяется как: 20*log(H(w))
![]()
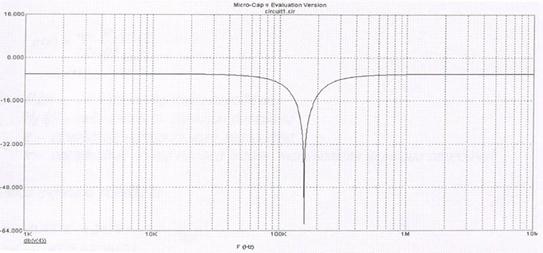
Рис 6. Логарифмическая АЧХ.
По графику определяем крутизну среза Sсреза=70 дБ/дек, что соответствует Sсреза =21 дБ/окт.
5. Импульсная и переходная характеристики. Графики характеристик
5.1 Импульсная характеристика цепи
Импульсную характеристику посчитаем по формуле:
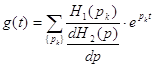
где H1(p) – числитель функции передачи;
H2(p) – знаменатель функции передачи;
e – основание натурального логарифма;
k – порядковый номер полюса.
Полюса функции передачи:
p1=![]()
p2=![]()
p3=![]()
p4=![]()
H1=p4 + 2p2 + 1
H2=p4 + 2.8284p3 + 5.999p2 + 2.8284p + 2
g(t)=![]()
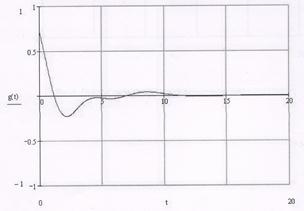
Рис 7. График импульсной характеристики цепи.
5.2 Переходная характеристика цепи.
Связь между импульсной и переходной характеристиками:
![]()
![]()
Получаем график:
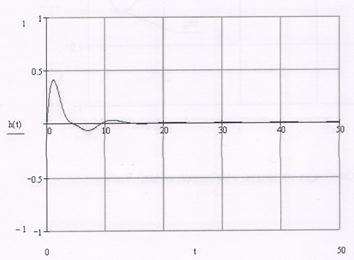
Рис 8. График переходной характеристики цепи.
Для наглядности и сравнения приведем оба графика в одной системе координат:
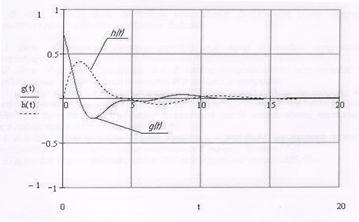
Рис 9. Графики переходной и импульсной характеристик цепи.
Заключение
В ходе работы были проведены все необходимые вычисления и по полученным результатам можно сделать выводы:
1. Данный фильтр является полосно-задерживающим или режекторным. Об этом наглядно свидетельствует график АЧХ.
2. Цепь является устойчивой, т.к. в правой полуплоскости нет полюсов. Действительные части полюсов отрицательные, следовательно, все процессы затухают.
3. Цепь является минимально-фазовой, т.к. нули в правой полуплоскости отсутствуют.
4. Все свободные процессы в цепи затухают – это видно из графика переходной характеристики.
5. Крутизна среза S=70 дБ/дек, время задержки сигнала ![]()
У таких фильтров, чем резче разграничиваются друг от друга полосы непропускания, тем больше фильтрующее действие фильтра, тем больше его избирательность, тем лучше частотная характеристика фильтра – кривая зависимости тока через фильтр или его затухания от частоты. В случае идеального режекторного фильтра частотная характеристика имела бы вид прямоугольника.
Литература
1. Коровин, В.М. Анализ линейных цепей с применением микрокалькуляторов: учебное пособие к курсовой работе. /В.М. Коровин – Челябинск: ЧПИ, 1988.
2. Стандарт предприятия. Курсовое и дипломное проектирование. Общие требования к оформлению. СТП ЮУрГУ 04-2001/Составители: Сырейщикова Н.В., Гузеев В.И., Сурков И.В., Винокурова Л.В., - Челябинск: ЮУрГУ, 2001.
3. Матханов, П.Н. Основы анализа электрических цепей: линейные цепи./П.Н. Матханов. – М: «Высшая школа», 1981.
4. Коровин, В.М. Схемотехническое проектирование. Теоретические основы: учебное пособие. Ч.2. / В.М. Коровин. – Челябинск: ЧГТУ, 1993.
5. Попов, В.П. Основы теории цепей./В.П. Попов. – Москва: «Высшая школа», 2003.
Похожие работы
... ЦЕПИ Начертим схему цепи по которой можно определить коэффициент передачи и обозначим узлы: Рис.2 Схема фильтра. Воспользуемся упрощенным вариантом определения функции передачи обратимой цепи, где за основу примем диагональную матрицу собственных проводимостей узлов, умножив для удобства все ее элементы на частоту p: - звездное число. Произведем нахождения дифференцируемой , это ...
... механизма для обеспечения эффективного перехода на различные способы транспортирования в зависимости от свойств материала и выполняемой технологической операции. Разработке методов кинематического анализа механизмов транспортирования ткани швейных машин и соответствующего этой задаче алгоритмического и программного обеспечения посвящены работы. [67],[71],[72]. В работе Ю.Ю.Щербаня и В.А.Горобца ...
... к расчету. ¨ В оглавлении указываются названия разделов и номера страниц, соответствующие началам разделов. ¨ Во введении кратко рассматривается общенаучное значение теории электрических цепей (ТЭЦ) для изучения электромагнитных явлений и их практического приложения. Описываются связи ТЭЦ с соответствующими разделами математики и физики, а также с различными ...
... калькуляции представлены в табл.4.2. Ленточный график работ 5. Безопасность жизнедеятельности и охрана труда Дипломная работа посвящена анализу погрешностей волоконно-оптического гироскопа. В ходе ее выполнения были проведены необходимые расчеты и сделаны выводы, которые могут послужить материалом для ...
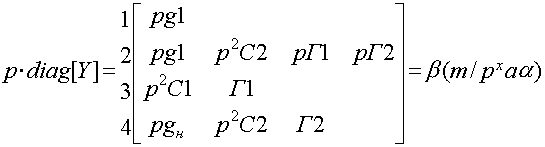
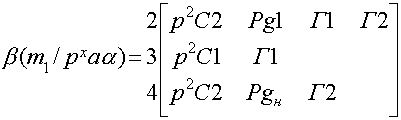
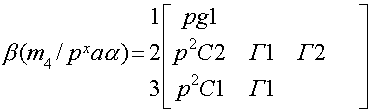



0 комментариев