Навигация
Влияние объемных сопротивлений транзисторов на погрешность перемножителя
3. Влияние объемных сопротивлений транзисторов на погрешность перемножителя
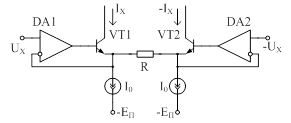
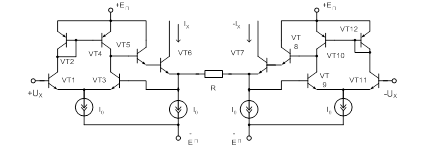
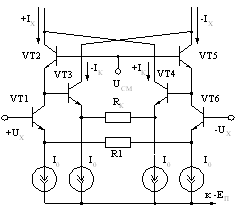
Транзисторы, используемые в АП, имеют ненулевые объемные сопротивления базы, что также приводит к появлению дополнительной погрешности. Оценить эту погрешность можно поочередно для двухквадрантной модели (для транзисторов VT1-VT4 и VT1, VT4-VT6, рис. 3.1), определив результирующую погрешность как сумму с учетом знаков приращений.
Для транзисторов VT1-VT4 при условии, что s1=s4 и s2=s3, можно записать:
 , (3.1)
, (3.1)
где IX1=IX0 +IX; IX2=IX0 -IX; IY1=IY0 - IY; IY2=IY0 -IY; IX, IY – соответствующие приращения токов относительно статических токов IX0 и IY0.
Если нормировать токи следующим образом:
IX1=IX0 (1+X); IX1=IX0 (1-X); IY1=IY01 (1+Z); IY1=IY01 (1+Z),
где Х=IX/IX0, Z=IY/IY0, то выражение (3.1) можно представить как
![]()
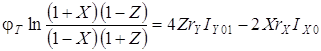 . (3.2)
. (3.2)
Из (3.2) следует, что при rX=rY=0 X=Z, а при ненулевых значениях объемных сопротивлений погрешность составит gО1=Z-X.
Тогда уравнение (3.1) преобразуется к виду:
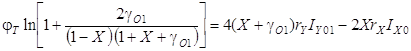 .
.
Полагая, что 1+gО1»1 (погрешность достаточно мала), а также положив, что rYIY01<<jT, получаем:
 . (3.3)
. (3.3)
Для другой части двухквадрантной модели, по аналогии с предыдущим случаем, учитывая соответствующие знаки приращений, получаем:
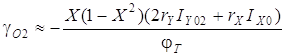 . (3.4)
. (3.4)
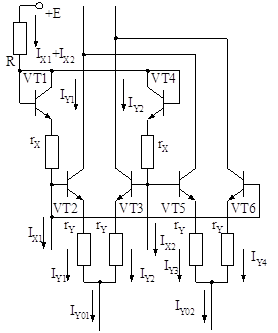
Рис. 3.1. Четырехквадрантная модель АП для оценки
влияния объемных сопротивлений на погрешность
Учитывая, что IY01=I0(1+Y), а IY02=I0(1-Y), для суммарной погрешности четырехквадрантной модели получим:
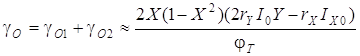 . (3.5)
. (3.5)
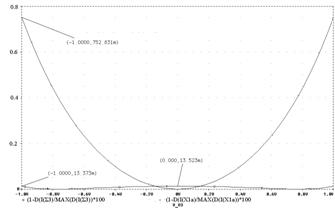
Выражение (3.5) показывает, что даже при идеальных характеристиках ПНТ и отсутствии остальных составляющих погрешности перемножителя погрешность gО может достигать 0,2 %. Уменьшить эту составляющую погрешности можно несколькими способами, которые в конечном счете сводятся к уменьшению до нуля второго сомножителя в выражении (3.5). Отметим, что достигать этого с помощью выбора разных токов I0 и нежелательно, так как в этом случае нарушается фазовая идентичность каналов X и Y, то есть I0 » IX0 [3]. У транзисторов, содержащихся в базовом матричном кристалле АБМК.1 (НПО «Интеграл»), объемные сопротивления довольно велики и имеют составляющую, зависящую от тока базы [12, 13]. В этом случае при выборе соответствующего отношения площадей транзисторов, входящих в множительное ядро, можно добиться минимизации погрешности. Например, для АБМК.1 можно считать оптимальным отношение s1/s2=3/4 при токах I0 » IX0 » 1 – 2 мА.
4 Компенсация температурной погрешности
Во втором разделе было получено выражение для масштабного коэффициента преобразования входных напряжений, которое зависит от тока источников тока ПНТ. С одной стороны, можно рекомендовать жесткую стабилизацию этих токов при изменении питающих напряжений и температуры. Если проблему стабилизации токов I0 при изменении питающего напряжения можно решить всего лишь стабилизацией напряжения питания, то проблема стабилизации тока при изменении температуры решается достаточно сложно.
Однако, поскольку масштабный коэффициент описывается довольно сложной функцией от температуры (зависит от jТ), используя источники тока с заданным температурным дрейфом, можно частично компенсировать изменение масштабного коэффициента при изменении температуры.
Можно рекомендовать следующую процедуру при проектировании источников тока для АП. В процессе схемотехнического моделирования определить температурный дрейф kT масштабного коэффициента при источниках тока, не имеющих температурного дрейфа, а затем выполнить источник тока по схеме, которая обеспечивает следующий закон изменения тока:
![]() ,
,
где I0(T0) – необходимый статический ток ПНТ при комнатной температуре Т0; Т – температура окружающей среды.
В этом случае удается значительно уменьшить средний температурный дрейф погрешности перемножения.
То есть задача проектирования источника тока сводится к выполнению источников тока с заданным значением начального тока и заданным температурным дрейфом. Поэтому задача построения таких источников тока требует самостоятельного дополнительного исследования.
Компенсация температурных погрешностей перемножителя является одной из сложных задач, требующих решения, которая в данной работе не рассматривается.
Похожие работы
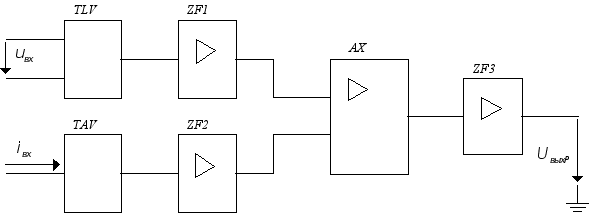
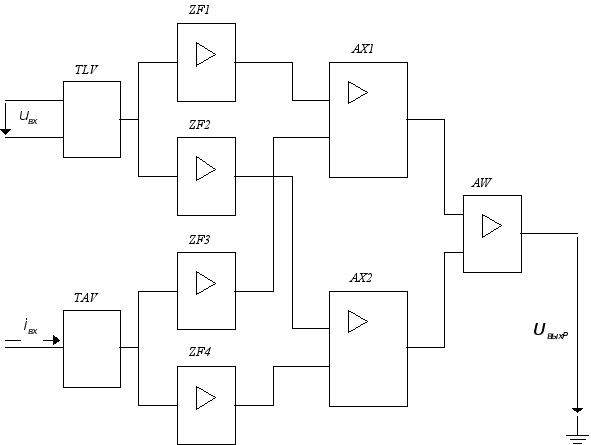
... ПЧФ, равным , то есть Сопротивление трансреактора TAV определяется тем же условием. При и Сопротивление вторичной обмотки трансреактора 4. Список используемой литературы Овчаренко Н. И. Проектирование аналоговых и цифровых измерительных преобразователей мощности. М.: Издательство МЭИ, 1994. Овчаренко Н. И. Аналоговые и цифровые измерительные преобразователи мощности автоматических ...
... преобразования в заданное число раз. Кроме того, динамический диапазон мостовых ПНТ по входному сигналу теоретически может достигать диапазона ±ЕП, что принципиально недостижимо в преобразователях напряжение-ток на основе дифференциального каскада. Это особенно важно при проектировании низковольтных прецизионных схем. На рисунке 12 представлены результаты моделирования схемы мостового ПНТ. ...
... . Для малых значений входных напряжений коэффициенты усиления ДК2 и ДК3: Так как выходы ДК2 и ДК3 соединены перекрестно, то их выходные напряжения вычитаются: . Таким образом, осуществляется перемножение входных сигналов. Так как , то , где коэффициент Выражение для U2 является точным только при малых значениях Ux и Uy, не превышающих примерно 20 мВ. При больших входных напряжениях ...
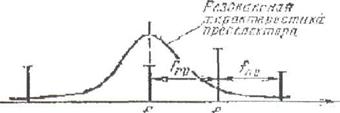
... сим=()*tg(k*l)/=(7,5/π)* tg(0,837*1,875)/7,5 =8,72*10-3м; Нд несим=0,5*Нд сим=4,36*10-3 м. UД=ЕД*НД=0,0000394*4,36*10-3=1,72*10-6 В Проверено выполнение следующего условия: UДUтр1,72*10-60,21*10-6. Из этого вытекает, что радиоприёмное устройство будет уверенно принимать сигнал. Рассчитано номинальное значение отношения сигнал/шум на входе приёмника: 9(1,72*10-6/0,21*10-6)2 = ...

0 комментариев