Навигация
Акустические свойства полупроводников
Министерство образования и науки Украины
Донецкий политехнический техникум
Кафедра физики
Реферат:
Акустические свойства полупроводников
Выполнил: Филенко М.С.
Проверил: Семенов А.И.
Донецк, 2002
План
1. КАК УСТРОЕН ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ПОЛУПРОВОДНИК
2. ПОГЛОЩЕНИЕ И УСИЛЕНИЕ ЗВУКА
3. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ ПРИ УСИЛЕНИИ ЗВУКА
4. УСИЛЕНИЕ АКУСТИЧЕСКИХ ШУМОВ И СВЯЗАННЫЕ С ЭТИМ ЯВЛЕНИЯ
5. ЗВУКОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
6. Заключение
1. КАК УСТРОЕН ПЬЕЗОЭЛЕКТРИЧЕСКИЙ
ПОЛУПРОВОДНИКМы уже говорили, что в полупроводниках имеет смысл изучать в первую очередь те акустические эффекты, которые обусловлены взаимодействием звука с электронами проводимости. Ведь именно небольшое число электронов проводимости отличает полупроводник от диэлектрика. Типичные концентрации электронов в тех случаях, которые нас будут интересовать, составляют 1011 - 1016 см-3.
Рассмотрим акустические эффекты только в одном типе полупроводников, а именно в пьезоэлектрических полупроводниках. Акустические эффекты в них наиболее ярко выражены, лучше и подробнее всего исследованы.
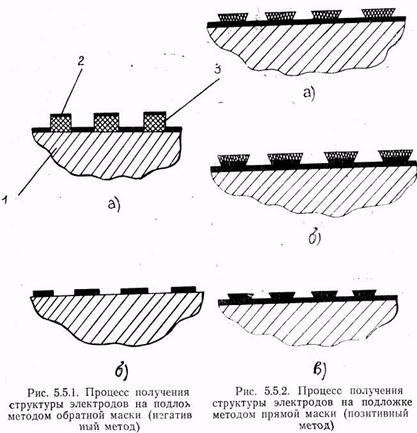
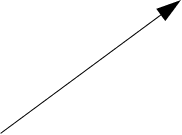
Пьезоэлектрики - это такие кристаллы, в которых под влиянием однородной деформации возникают дипольный момент, а значит, и электрическое поле, пропорциональные деформации. Наличие пьезоэлектрических свойств тесно связано с симметрией кристалла. Поясним это на модели ионной решетки, изображенной на рис. 1,а. На этом рисунке положительные попы закрашены. а отрицательные изображены светлыми кружками. Видно, что если эту решетку подвергнуть однородной деформации, то она не поляризуется (рис. 1,б). Рассмотрим теперь решетку, изображенную на рис, 2,а. Если эту решетку подвергнуть деформации растяжения в направлении, указанном стрелкой, то она поляризуется, поскольку «центры тяжести» положительных и отрицательных ионов при этом сдвигаются друг относительно друга (рис. 2, б, в). Наоборот, если поместить такую решетку в однородное электрическое поле, она деформируется. Деформация кристалла, пропорциональная приложенному электрическому полю, называется прямым пьезоэлектрическим эффектом; возникновение электрической поляризации при деформации — обратным пьезоэлектрическим эффектом.
Пьезоэлектрический эффект существует в целом ряде полупроводников — CdS, Zn0, GaAs, InSb, Те и др. Большинство опытов, в особенности на первом этапе, было проведено на CdS — этот полупроводник является довольно сильным пьезоэлектриком и в то же время фотопроводником (т. е. изменяет свою проводимость при освещении). Поэтому в нем, как уже говорилось, легко можно отделять электронные эффекты.
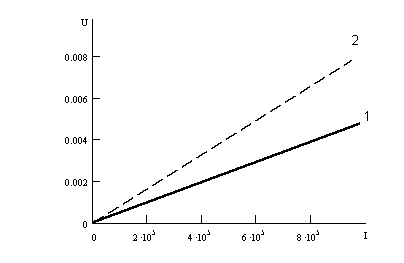
Если в пьезоэлектрике распространяется звук, т. е. волна деформации, то она сопровождается электрическими полями, обладающими пространственной и временной периодичностью звуковой волны. Эти поля продольные, т. е. параллельные направлению распространения звука. Можно сказать, что в пьезоэлектриках всякая звуковая волна сопровождается волной продольного электрического поля (мы его будем называть пьезоэлектрическим полем). В качестве оценки напряженности этих полей можно привести следующую цифру: при распространении звука в таком сильном пьезоэлектрике, как CdS, при плотности потока звуковой энергии S порядка 1 Вт/см2 амплитуда напряженности переменного поля может достигать нескольких сотен вольт на сантиметр.
Выясним теперь, как влияет пьезоэлектрический эффект на распространение звука в пьезодиэлектриках. Пусть продольный или поперечный звук распространяется в пьезодиэлектрике вдоль оси симметрии кристалла, которую назовем осью ОХ. Деформация в такой волне характеризуется величиной du/dx, где и{х) — смещение точки кристалла в звуковой волне. В непьезоэлектрическом кристалле при такой деформации возникает упругое напряжение S:
S = λ du/dxгде К — модуль упругости. Это соотношение выражает известный закон Гука. В пьезоэлектрике, как мы видели, при деформации возникает дипольный момент, на который действует электрическое поле Е. В результате при наличии поля Е в пьезоэлектрнке упругое напряжение равно:
S = λ du/dx + βE (1)
где β — так называемый пьезоэлектрический модуль. Кроме того, при деформации в пьезоэлектрике возникает дополнительная поляризация. Соответственно в обычном соотношении, связывающем электрическую индукцию D с напряженностью поля Е (D=εE, где ε — диэлектрическая проницаемость), появляется дополнительный член — 4лβ du/dx.
Для вычисления скорости звука в пьезодиэлектрике достаточно соотношение (1) и соотношение между D и Е подставить в уравнение теории упругости:
ρ d2u/dt2 = ds/dx
(ρ — плотность кристалла) и в уравнение Пуассона dD/dx = 0 (диэлектрик!). В результате несложных преобразований получается величина:
![]()
ωd = √ λ ⁄ ρ * (1 + χ)½ , χ = 4πβ²/ελ (2)
Первое слагаемое в выражении для ωd дописывает вклад от близкодействующих упругих сил, которые существуют и в непьезоэлектриках. Второе обусловлено .дополнительными квазиупругими силами, связанными с пьезоэлектрическими полями. Таким образом, роль пьезоэлектрического эффекта определяется величиной χ , которую мы назовем коэффициентом пьезоэлектрической связи. В большинстве известных пьезоэлектрических полупроводников χ не превышает 0,1. Поэтому величину χ можно считать малым параметром теории, что мы и будем делать в дальнейшем. Так, вместо (2) имеем:
![]()
ωd = ω0(1 + χ/2), ω0 = √ λ ⁄ ρ
Обратимся теперь к пьезополупроводникам. Как взаимодействуют электроны проводимости с пьезоэлектрическим полем? Предположим сначала, что звук «замер» — создана периодическая в пространстве статистическая деформация:
u(x) = u0 cos qx.
В пьезодиэлектрике из уравнения Пуассона мы сразу бы получили: E = 4πβ du/dx ε. Электрический потенциал поля φ был бы при этом равен (Е = — dφ/dx).
φ0 = 4πβu / ε
А что будет с электронами в полупроводнике? Они перераспределятся в пространстве, стремясь стечь с потенциальных «горбов» и заполнить потенциальные «ямы». При этом уменьшится первоначальный потенциал (φ0, или, как говорят, произойдет его экранирование электронами проводимости. Поэтому первый вопрос, который следует решить: как перераспределяются электроны в поле потенциала и каким образом они его будут экранировать? Для решения этого вопроса следует выяснить, как нужно описывать движение электрона в поле звуковой волны. Это существенно зависит от того, какова величина соотношения между длиной звуковой волны 2л/q и длиной l свободного пробега электронов — какова величина параметра ql. Этот параметр играет центральную роль в теории акустических свойств проводников; при различных его значениях электроны по-разному взаимодействуют со звуком. Обычно в пьезоэлектрических полупроводниках ql «1, поэтому пока ограничимся рассмотрением этого случая. В чистых металлах при низких температурах может выполняться противоположное неравенство. Об этом пойдет речь в следующей главе.
Условие ql «1 означает, что на расстояниях порядка длины звуковой волны электрон успевает много раз столкнуться. В процессе столкновений устанавливается равновесное распределение электронов — электроны лишены индивидуальности, и их можно описывать как объемный заряд, характеризуемый электропроводностью о и коэффициентом диффузии D. В результате плотность тока j можно записать в виде:
j = σ (- dφ/dx) – e D dn/dx
где n — концентрация электронов. В стационарном состоянии плотность тока j в отсутствие внешнего электрического поля должна обращаются в нуль. Потому
n – n0 = - σφ / e D ,
где n0 - равновесная концентрация электронов. Если это выражение подставить в уравнение Пуассона, имеющее в полупроводнике вид:
dD/dx = 4π(n – n0)e ,
и использовать выражение для D, то сразу получим:
φ = φ0 (qR)2 / (1 + ((qR)2) (3)
Здесь - радиус экранирования Дебая — Хюккеля, равный
![]()
![]() R = √ εD/4πσ = √ εκΤ/4πe²n0 (4)
R = √ εD/4πσ = √ εκΤ/4πe²n0 (4)
(Τ — температура, κ — постоянная Больцмана).
Таким образом видно, что степень экранирования пьезоэлектрнческого потенциала определяется соотношением между длиной волны 2π/q и радиусом экранирования R.. Обычно говорят о дебаевском экранировании, когда речь идет, например, о кулоновском поле иона: поле «голого» заряда 1/r в результате экранирования приобретает вид: 1/r ехр(- r / R ), В данном же
случае речь идет об экранировании пространственно-периодического потенциала. При qR «1 устанавливается почти полное экранирование, и φ « φ0. Наоборот при qR »1 перераспределение электронов в пространстве почти не реагирует на коротковолновый звук. Соотношение (3) можно понять еще и следующим образом. В стационарном состоянии имеет место равновесие тока проводимости (вызванного наличием поля) и диффузионного тока (вызванного перераспределением электронов в пространстве). Поэтому электроны перераспределяются тем в большей степени, чем больше отношение электропроводности к коэффициенту диффузии (т. е. чем меньше R при заданной величине q). В свою очередь, чем больше электронов перераспредели-
лось в пространстве, тем более эффективно экранирование затравочного потенциала φ0.
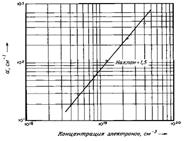
Приведем характерные значения радиуса экранирования в типичных случаях. В CdS при комнатной температуре и n0 = 1012 см-3 R = 5 * 10-4 см: при n0 =1014 см-3 R = 5 * 10-5 см.
Учтем теперь, что бегущая звуковая волна не стоит на месте, а распространяется по кристаллу, создавая электрическое поле, меняющееся в каждой точке кристалла с частотой звука ω². Поэтому возникает вопрос, за какое же время устанавливается статическая картина экранирования, описанная выше. Таким характерным временем является максвелловское время релаксации:
τ = ε/4πσ
Оно обратно пропорционально электропроводности σ, что естественно: ведь именно благодаря процессам электропроводности электроны проводимости могут перераспределяться в пространстве.
Если величина ωτ мала, то за период звука статическое экранирование успевает установиться почти полностью, и картина пространственного распределения электронов мало отличается от той, которая была бы в статическом случае. При этом, как мы видели, потенциал φ отличается от φ0 множителем (qR)2 [1 + (qR)2 ]-1. Такой же множитель должен появиться и в слагаемом, описывающем вклад в скорость звука за счет пьезоэлектрического эффекта:
ω = ω0 [1 + χ (qR)2 /2 (1 + (qR)2 )]
В обратном предельном случае, когда ωτ »1, экранирование не успевает установиться, и скорость звука в полупроводнике равна ωd.
Похожие работы
... а также других магнитных материалов и зависит от спонтанной намагниченности и напряженности внешнего магнитного поля. В зависимости от природы кристалла, по которому распространяется акустическая волна, механизм ее взаимодействия с электронами проводимости может быть различным. Рассмотрим вначале металлический звукопровод. Представим его в виде одномерной цепочки положительно заряженных ионов, ...
... поглощения к неизвестному. 6. Пример расчета спектральной зависимости коэффициента поглощения селективно поглощающего покрытия в видимой и ИК части спектра Более полные теоретические выкладки с пояснениями вы можете найти в [4]. Зададим толщину мультипленки и количество пленок входящих в ее состав: Определим комплексный показатель преломления (в мультипленке две пленки - q): ...
... граничное условие заключается в отсутствии механических напряжений. Граничным условием для вектора электрической индукции является непрерывность его нормальных составляющих в отсутствии поверхностных зарядов. Поверхностные акустические волны (ПАВ), упругие волны, распространяющиеся вдоль свободной поверхности твердого тела или вдоль границы твердого тела с другими средами и затухающие при ...
... (ПАВ) поставило задачу о необходимости тщательного анализа процессов возбуждения, распространения и рассеяния ПАВ неоднородностями и искусственными дефектами на поверхности твердого тела. В основе функционирования большинства устройств обработки сигналов на ПАВ лежит взаимодействие последних с различного рода управляющими неоднородностями в виде выступов, канавок, поверхностных электродов, ...

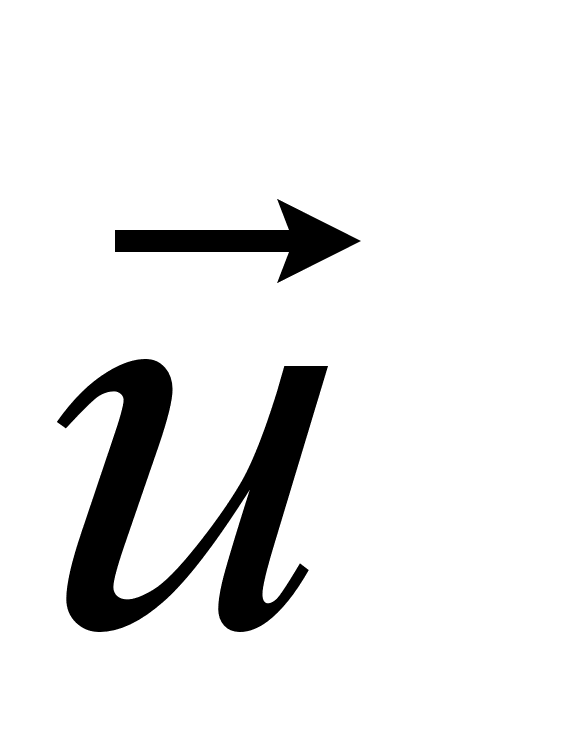
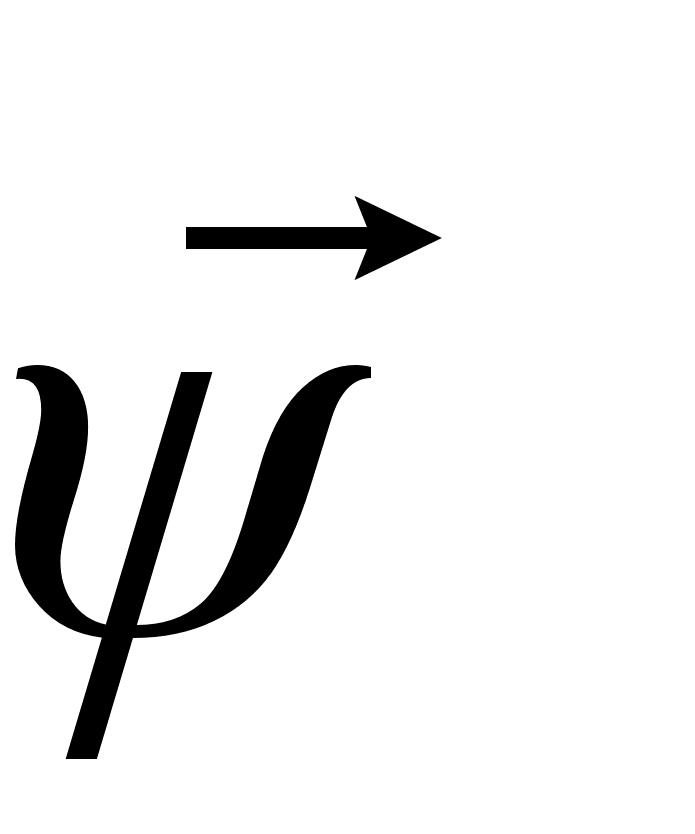
0 комментариев