Навигация
ПОГЛОЩЕНИЕ И УСИЛЕНИЕ ЗВУКА
2. ПОГЛОЩЕНИЕ И УСИЛЕНИЕ ЗВУКА
При распространении бегущей звуковой волны пространственное распределение электронов стремится следовать за пространственным распределением пьезоэлектрического потенциала. Соответственно переменные пьезоэлектрические поля порождают переменные электронные токи, которые и «подстраивают» распределение электронов к распределению потенциала. При протекании этих токов в проводнике должно выделяться джоулево тепло. В результате при распространении звука механическая энергия звуковой волны переходит в энергию беспорядочного теплового движения, т. е. происходит поглощение звука. Интенсивность поглощаемого звука изменяется по закону:
S (х) =S (0) ехр( - Гх),
где S(0) — интенсивность «на входе» кристалла. Величина Г называется коэффициентом поглощения звука.
Для отношения коэффициента поглощения звука Г к величине его волнового вектора q можно получить следующее выражение:
Г / q = χωτ/((1 + q2R2)2 + (ωτ) 2) (5)
Частотной зависимости этого выражения можно дать следующее наглядное объяснение.
Переменный ток, создаваемый пьезоэлектрическим почтем, вызывает перераспределение свободных зарядов. Перераспределенные заряды, в свою очередь, создают добавочное электрическое поле. Оно, как уже говорилось, направлено противоположно первоначальному электрическому, полю и, следовательно, приводит к уменьшению тока проводимости; τ и есть то время, за которое происходит перераспределение свободных зарядов. При статической деформации заряды перераспределяются и их поле компенсирует (экранирует) пьезоэлектрическое поле. таким образом, что ток становится равным нулю.
Если деформация измеряется с частотой ω, которая гораздо меньше 1/ τ, устанавливается почти полная компенсация. Точнее, поле объемных зарядов в случае переменной деформации, создаваемой звуком, отличается от статического поля на малую величину, пропорциональную ωτ. Поэтому в пьезоэлектрике протекает переменный ток, пропорциональный той же малой величине ωτ. Соответственно коэффициент Г, определяемый квадратом плотности тока, оказывается пропорциональным ω2.
В обратном предельном случае больших ωτ поле объемных зарядов за период звука вообще не успевает возникнуть. Поэтому при ωτ »1 коэффициент пропорциональности между плотностью тока и электрическим полем оказывается вообще независящим от частоты. Не зависит от частоты и коэффициент Г. Член (ωτ) 2 в знаменателе (5) и обеспечивает предельный переход от одного случая к другому. . Наконец, при qR » 1 коэффициент поглощения быстро убывает при увеличении частоты. Это связано с тем (уже отмечавшимся выше) обстоятельством, что звуковая волна, длина которой гораздо меньше радиуса экранирования, почти не вызывает перераспределения заряда даже в статическом случае.
Коэффициент поглощения достигает максимального значения при частоте ωm = ω0/R, т. е. когда длина волны равна 2πR; максимальное значение Гmo коэффициента поглощения равно χ/4R.
Характер частотной зависимости коэффициента поглощения определяется величиной ωmτ. Если ωmτ « 1, то максимум получается сравнительно острым.
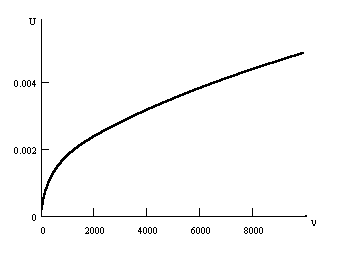
В противоположном предельною случае коэффициент поглощения растет пропорционально ω2 вплоть до частот порядка 1/τ, после чего его рост становится очень медленным. Максимум в этом случае оказывается более пологим. При ω » ωm коэффициент поглощения во всех случаях убывает пропорционально ω2. Семейство Г(ω) при разных значениях ωmτ приведено на рис. 3.
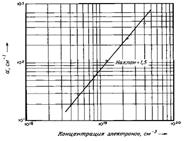
Интересно проследить характер зависимости коэффициента поглощения Г от электронной концентрации n0. Обычно проводимость σ пропорциональна n0: σ = е n0μ, где μ - так называемая подвижность электронов. Таким образом, максвелловское время релаксации τ обратно пропорционально n0. Радиус экранирования R, как мы видели, обратно пропорционален √ n0 (см. (4)). Поэтому при малых концентрациях электронов коэффициент Г прямо пропорционален n0, а при больших - обратно пропорционален n0. Существует, таким образом, при любой частоте (о некоторая промежуточная концентрация nw, при которой коэффициент Г максимален.
Оценим коэффициент поглощения Г для какого-нибудь типичного случая. Рассмотрим, например, поперечный звук в CdS, скорость которого ω0 = 1,8 х 105 см/с. Пусть n0 = 5 х 1012 см-3, ω = 3 х 108 с-1, μ = 300 см2/Вс, χ = 0,036, ε = 9,4, Т=300 К. Тогда τ = 3,5 х 10-9 с, R= 1,6 х 10-4 см, q= 1,7 х 103 см-1, и мы получаем, что коэффициент Г составляет около 30 см-1. Это означает, что на расстоянии в 1/30 ~ 0,03 см интенсивность звука затухает в с раз, т. е. теория предсказывает сильное затухание уже при таких малых концентрации и частоте.
А теперь мы переходим, пожалуй, к самому интересному вопросу — анализу влияния электрического поля на поглощение звука. Представим себе, что к пьезоэлектрическому полупроводнику, в котором распространяется звуковая волна, приложено постоянное электрическое поле Е.
Под влиянием постоянного поля Е возмущения электронной концентрации, созданные звуковой волной, движутся со скоростью дрейфа электронов:
V = μE
Чтобы в этом случае найти изменение электронной концентрации под влиянием переменного поля звуковой волны, удобно перейти к движущейся системе координат, скорость которой по отношению к кристаллической решетке равна V. В этой системе можно пользоваться выражениями для распределения электронной концентрации, полученными в отсутствие постоянного электрического поля. Нужно только учесть, что в силу эффекта Доплера частота звука в движущейся системе координат изменяется и оказывается равной ω — qV, где q — волновой вектор звука. В итоге в выражении (5) для отношения Г/q следует произвести замену ω → ω - qV. Это дает:
Г/q = χω(ω – qV)τ/ω0((1 + q2R2) + (ω – qV2)τ2)
В простейшем случае, когда направление распространения звука параллельно дрейфовой скорости, коэффициент поглощения обращается в нуль при V = ω, т. е. когда дрейфовая скорость электронов становится равна скорости звука. При V > ω коэффициент поглощения меняет знак. При Г<0 плотность потока звуковой энергии изменяется по закону:
S(x)=S(0)exp (-Гх) = S(0) ехр (│Г│х).
т. е. поглощение звука сменяется его усилением.
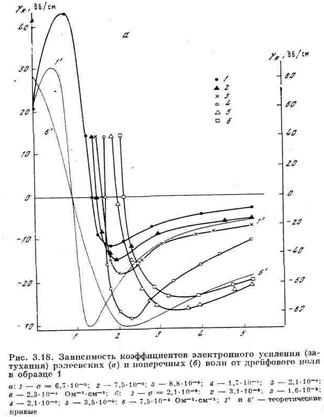
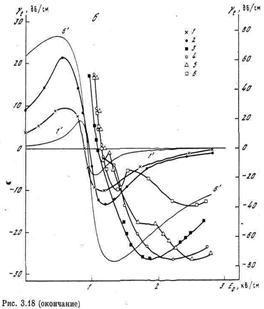
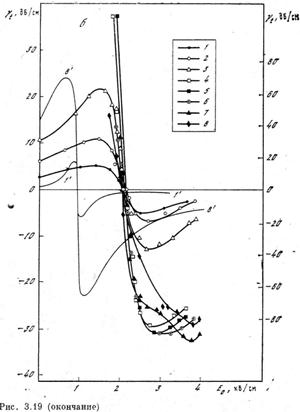
Зависимость коэффициента поглощения от постоянного электрического поля (точнее, от дрейфовой скорости электронов) приведена на рис. 4. Видно, что кривая зависимости Г(V) антисимметрична относительно линии V = ω. Отметим еще одно важное обстоятельство: если при распространении в прямом направлении (направлении дрейфа) звук усиливается, то при распространении в обратном направлении он обязательно затухает. Однако коэффициент поглощения при этом может быть меньше коэффициента усиления при прямом прохождении.
При неизменной дрейфовой скорости V коэффициент усиления как функция частоты достигает максимума при ω = ωm как и в случае поглощения звука. Абсолютный максимум коэффициента усиления по отношению к изменению и частоты и дрейфовой скорости при заданной концентрации равен опять-таки Гmo — максимальному значению коэффициента поглощения.
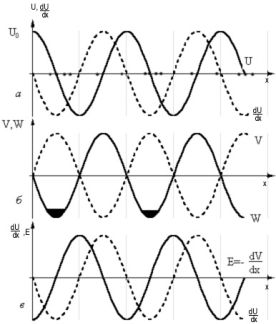
В чем физическая основа усиления звука? Для того чтобы ответить на этот вопрос, посмотрим на поглощение звука с несколько иной точки зрения. Можно сказать, что поглощение звука определяется фазовым сдвигом между деформацией решетки ди/дх и пьезоэлектрическим полем Е. В пьезодиэлектрике фазовый сдвиг отсутствует, и пьезоэлектрический эффект не приводит к поглощению звука - он лишь изменяет эффективную жесткость решетки (скорость звука). В пьезополупроводнике пьезоэлектрическое поле отстает по фазе от деформации решетки. Соответствующий сдвиг фаз пропорционален ют; этой же величине пропорционален коэффициент поглощения. При включении электрического поля возмущения концентрации электронов, созданные звуковой волной, дрейфуют со скоростью V. Это приводит к уменьшению сдвига фаз и, следовательно, к уменьшению поглощения. В более сильных электрических полях пьезоэлектрическое поле опережает по фазе деформацию решетки. При этом происходит передача энергии электрического поля звуковой волне — ее интенсивность нарастает. Именно эти процессы математически описываются формулой (6).
До сих пор мы в наших рассуждениях не учитывали поглощения звука кристаллической решеткой. Чтобы его учесть, нужно к выражению для коэффициента электронного поглощения звука добавить коэффициент решеточного поглощения. В результате значение коэффициента поглощения оказывается больше, а коэффициента усиления — меньше, .чем в отсутствие решеточных эффектов. Полный коэффициент усиления обращается в нуль не при каком-нибудь одном, а при двух значениях дрейфовой скорости — Vl и Vll на рис. 4.
Оценим коэффициент усиления в каком-нибудь типичном случае. Обратимся с этой целью к примеру, рассмотренному на стр. 16. При (Vω)/ω)== 0,l мы получаем, что Г~5 см-1. Если увеличить дрейфовую скорость и рассмотреть случай {Vω)/ω = 1, то Г~30 см-1. Это значит, что интенсивность звука возрастает в е раз на расстоянии в 1/30~0,03 см. При дальнейшем возрастании дрейфовой скорости коэффициент усиления начинает убывать.
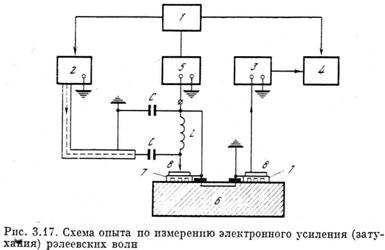
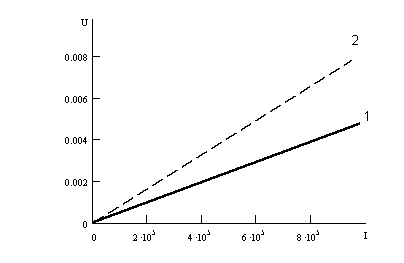
Приведем в качестве примера экспериментальные зависимости коэффициента поглощения (усиления) от электрическою поля, наблюдавшиеся в кристалле CdS (рис. 5). Как уже говорилось, CdS—фотопроводник. Начало отсчета затухания на рис. 5 соответствует затуханию в неосвещенном образце. При изменении уровня освещенности изменяется проводимость кристалла, а следовательно, и т. Так получены кривые В и С, соответствующие частоте 45 МГц и значениям (от 4,2 и 4,8 соответственно. Кривая А получена на частоте 15 МГц; <от=0,83. Из рисунка видно, что при значении электрического поля ~750 В/см коэффициент поглощения изменяет знак—поглощение сменяется усилением.
Обратим внимание на то, что теория дает очень большие значения коэффициента усиления. Усиление звука в пьезополупроводниках наблюдалось в целом ряде экспериментальных работ. В некоторых случаях существующая теория удовлетворительно описывала данные опыта. Иногда, однако, усиление, наблюдавшееся экспериментально, оказывалось гораздо меньше теоретического. Такое расхождение, возможно, связано с решеточным поглощением звука и некоторыми другими явлениями (которые не учтены в этом простейшем варианте теории).
А может быть, дело здесь в следующем. В простейшей теории, описанной выше, предполагается, что изменение концентрации электронов и электрического поля пропорционально деформации решетки в звуковой волне (линейная теория). При больших амплитудах звуковой волны линейный закон становится неприменимым — в таком случае говорят, что имеют место нелинейные эффекты. В процессе усиления звука его интенсивность может возрасти на много порядков, поэтому такие эффекты могут быть важны. О нелинейных эффектах речь пойдет ниже, и мы увидим, что они могут существенно изменить картину усиления звука.
При приложении к пьезополупроводнику электрического поля изменяется не только поглощение. Изменяя сдвиг фаз между волнами деформации и пьезоэлектрического поля, внешнее электрическое поле изменяет л скорость звука.
Отметим, что скорость звука зависит не только от величины, но и от направления электрического поля по отношению к направлению распространения звука. Соответственно скорости волн, распространяющихся вдоль и навстречу полю, различны. Это обстоятельство полезно иметь в виду; мы вспомним о нем в следующем разделе.
Похожие работы
... а также других магнитных материалов и зависит от спонтанной намагниченности и напряженности внешнего магнитного поля. В зависимости от природы кристалла, по которому распространяется акустическая волна, механизм ее взаимодействия с электронами проводимости может быть различным. Рассмотрим вначале металлический звукопровод. Представим его в виде одномерной цепочки положительно заряженных ионов, ...
... поглощения к неизвестному. 6. Пример расчета спектральной зависимости коэффициента поглощения селективно поглощающего покрытия в видимой и ИК части спектра Более полные теоретические выкладки с пояснениями вы можете найти в [4]. Зададим толщину мультипленки и количество пленок входящих в ее состав: Определим комплексный показатель преломления (в мультипленке две пленки - q): ...
... граничное условие заключается в отсутствии механических напряжений. Граничным условием для вектора электрической индукции является непрерывность его нормальных составляющих в отсутствии поверхностных зарядов. Поверхностные акустические волны (ПАВ), упругие волны, распространяющиеся вдоль свободной поверхности твердого тела или вдоль границы твердого тела с другими средами и затухающие при ...
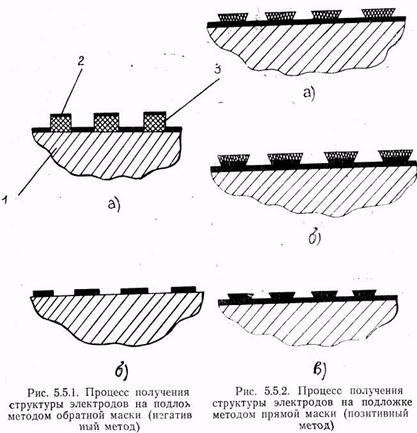
... (ПАВ) поставило задачу о необходимости тщательного анализа процессов возбуждения, распространения и рассеяния ПАВ неоднородностями и искусственными дефектами на поверхности твердого тела. В основе функционирования большинства устройств обработки сигналов на ПАВ лежит взаимодействие последних с различного рода управляющими неоднородностями в виде выступов, канавок, поверхностных электродов, ...

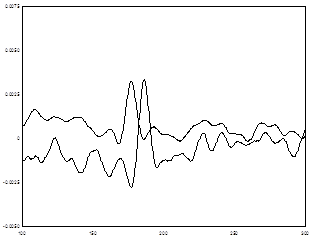
0 комментариев