Навигация
Анализ динамического поведения механической системы
Содержание:
Аннотация
Исходные данные
1. Применение основных теорем динамики механической системы
1.1 Постановка второй основной задачи динамики системы
1.2 Определение закона движения системы
1.3 Определение реакций внешних и внутренних связей
2. Построение алгоритма вычислений
3. Применение принципа Даламбера-Лагранжа и уравнений Лагранжа второго рода.
3.1 Составление дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
Анализ результатов
Аннотация
Дана механическая система с одной степенью свободы, представляющая собой совокупность абсолютно твердых тел, связанных друг с другом посредством невесомых растяжимых нитей, параллельных соответствующим плоскостям. Система снабжена внешней упругой связью с коэффициентом жесткости с. На первое тело системы действует сила сопротивления ![]() и возмущающая гармоническая сила
и возмущающая гармоническая сила ![]() . Трением качения и скольжения пренебрегаем. Качение катков происходит без скольжения, проскальзывание нитей на блоках отсутствует. Применяя основные теоремы динамики системы и аналитические методы теоретической механики, определен закон движения первого тела и реакции внешних и внутренних связей. Произведен численный анализ полученного решения с использованием ЭВМ.
. Трением качения и скольжения пренебрегаем. Качение катков происходит без скольжения, проскальзывание нитей на блоках отсутствует. Применяя основные теоремы динамики системы и аналитические методы теоретической механики, определен закон движения первого тела и реакции внешних и внутренних связей. Произведен численный анализ полученного решения с использованием ЭВМ.
Исходные данные:
|
|
|
|
|
|
|
|
|
|
|
|
|
| m = 1 кг |
|
|
| r = 0.1 м | с = 4000 H/м |
|
|
|
|
Часть 1. Применение основных теорем динамики механической системы
1.1 Постановка второй основной задачи динамики системы.
Расчетная схема представлена на рисунке 1.
Здесь обозначено:
![]() ;
; ![]() ;
; ![]() - силы тяжести;
- силы тяжести;
![]() - нормальная реакция опорной плоскости;
- нормальная реакция опорной плоскости;
![]() - сила сцепления;
- сила сцепления;
![]() - упругая реакция пружины;
- упругая реакция пружины;
![]() - реакция подшипников;
- реакция подшипников;
![]() - сила вязкого сопротивления;
- сила вязкого сопротивления;
![]() - возмущающая сила.
- возмущающая сила.
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка (3) происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза (1).
Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в форме:
![]()
![]() - сумма мощностей внешних сил;
- сумма мощностей внешних сил;
![]() - сумма мощностей внутренних сил;
- сумма мощностей внутренних сил;
Тогда кинетическая энергия системы равна сумме кинетических энергий тел,
(1.2) ![]()
(1.3) Груз (1) совершает поступательное движение, ![]()
![]() ;
;
(1.4) Блок (2) совершает вращательное движение, ![]()
![]() , где
, где ![]()
(1.5) Каток (3) совершает плоскопараллельное движение, ![]()
![]() , где
, где ![]()
Кинетическая энергия всего механизма равна:
(1.6) ![]() ;
;
Выразим – через скорость груза (1)
![]()
![]()
![]()
(1.7) ![]() ;
; ![]() ;
;
Подставляя кинематические соотношения (1.7) в выражение (1.6), получаем:
(1.8) ![]()
(1.9) ![]()
![]() ;
;
Найдем производную от кинетической энергии по времени:
(1.10) ![]()
Вычислим сумму мощностей внешних и внутренних сил. Мощность силы равна скалярному произведению вектора силы на скорость в точке ее приложения;
(1.11) ![]()
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемые и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
(1.12) ![]() = 0;
= 0;
Будут равняться нулю и мощности следующих внешних сил, приложенных в точках, скорости которых равны нулю:
![]()
Сумма мощностей остальных внешних сил:
(1.13) ![]()
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил определим:
(1.14) ![]()
где ![]() приведенная сила.
приведенная сила.
Упругую силу считаем пропорциональной удлинению пружины, которое равно сумме статического ![]() и динамического
и динамического ![]() удлинений:
удлинений:
(1.15) ![]()
Сила вязкого сопротивления ![]() , тогда
, тогда
(1.16) ![]()
В состоянии покоя системы приведенная сила равна нулю. Полагая в (1.16) S=0, ![]() =0 и F(t)=0, получаем условие равновесия системы:
=0 и F(t)=0, получаем условие равновесия системы:
(1.17) ![]()
Отсюда статическое удлинение пружины равно:
(1.18) ![]()
Подставляя (1.18) в (1.16), получаем окончательное выражение для приведенной силы:
(1.19) ![]()
Подставив выражения для производной от кинетической энергии и сумму мощностей всех сил с учетом (1.19) в (1.1), получаем дифференциальное уравнение движения системы:
(1.20) ![]()
(1.21) ![]()
где k циклическая частота свободных колебаний;
![]()
n – показатель степени затухания колебаний;
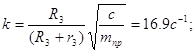
Похожие работы
... груза, его скорости и ускорения, а также динамических реакций внешних и внутренних связей. Результаты расчетов: 5. Анализ результатов вычислений Математическая модель, описывающая поведение исследуемой механической системы, построена при следующих основных допущениях: ...
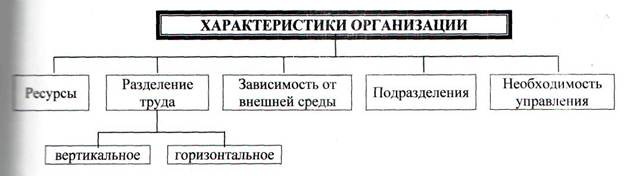
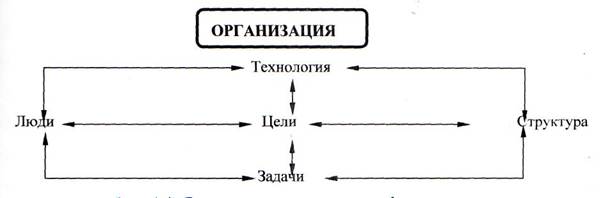
... полномочий. Оперативность структуры означает возможность реакции системы на изменения обстановки, временные показатели этой реакции и ее цену. Типичным примером организации как сложной системы является производственно-экономическая система (ПЭС). Основным видом производственно-экономических систем является предприятие. Приведем, применительно к промышленному предприятию, некоторые необходимые ...
... второй части курсовой работы и разработать проект с предложением соответствующих рекомендаций для эффективности его введения. 2 Анализ и оценка эффективности системы управления торгового предприятия (ИП Иванова А.А.) 2.1 Характеристика предприятия ИП Иванова А.А. Предприятие ИП Иванова А.А. находится в г. Шарыпово по адресу ул. Заводская, 8. Вблизи него располагается ...
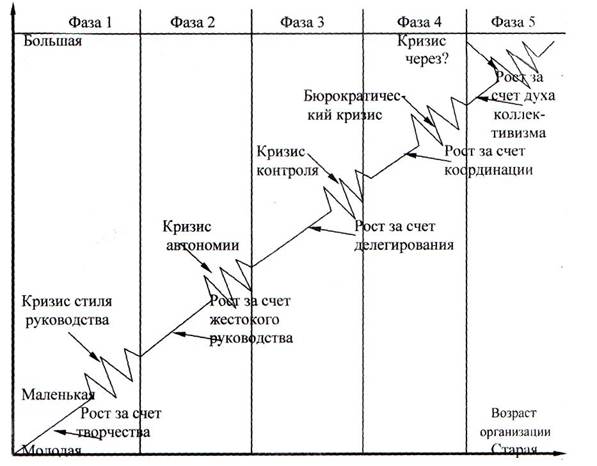
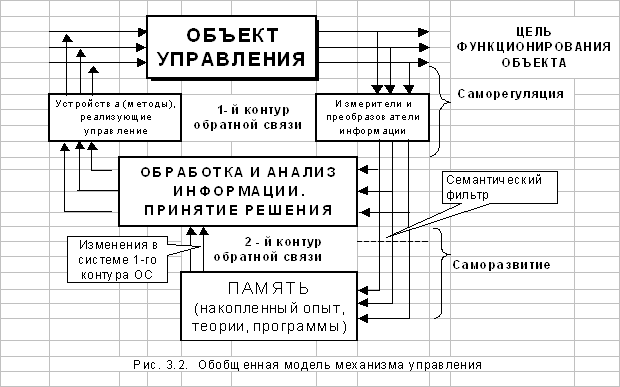
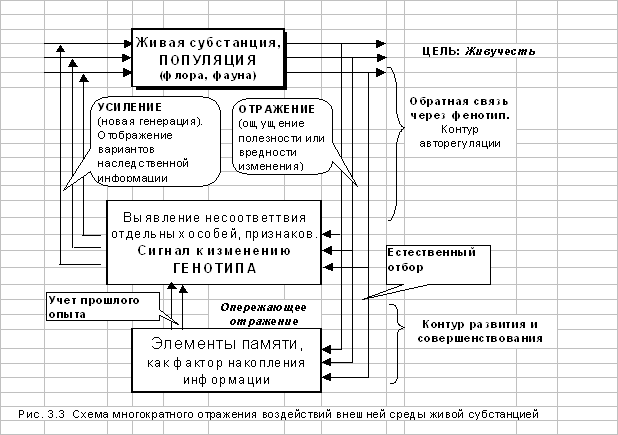
... Возникшие потребности в научно обоснованных методах и средствах управления нашли свое выражение в кибернетике - науке об управлении и системном анализе, особым предметом исследования которых являются сложные и очень сложные системы окружающего мира. 4.4 Организационные системы Традиционно современная кибернетика рассматривала, в основном, простые и сложные управляемые системы, для которых ...
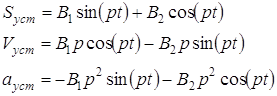
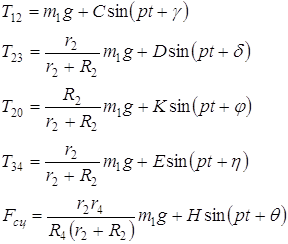





0 комментариев