Навигация
Определение закона движения системы
1.2 Определение закона движения системы
Проинтегрируем дифференциальное уравнение (1.20). общее решение этого неоднородного уравнения складывается из общего решения однородного уравнения ![]() и частного решения неоднородного
и частного решения неоднородного ![]() :
:
S = ![]() +
+ ![]() ;
;
Однородное дифференциальное уравнение, соответствующее данному неоднородному, имеет вид: ![]()
Составим характеристическое уравнение и найдем его корни:
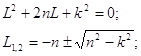
т.к. n < k => решение однородного уравнения имеет вид:
![]()
где ![]() частное решение дифференциального уравнения ищем в виде правой части:
частное решение дифференциального уравнения ищем в виде правой части: ![]()
![]() далее получаем:
далее получаем:
![]()
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения состояния А и В
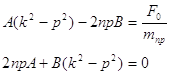
Решая эту систему получаем следующие выражения:
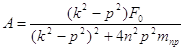 А = 0.04 м;
А = 0.04 м;
![]() В = - 0.008 м;
В = - 0.008 м;
Общее решение дифференциального уравнения:

Постоянные интегрирования ![]() определяем из начальных условий, при t = 0 имеем:
определяем из начальных условий, при t = 0 имеем:
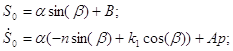
Решая эту систему получаем:
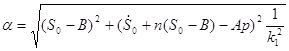
![]()
![]()
![]()
1.3 Определение реакций внешних и внутренних связей
Для решения этой задачи расчленим механизм на отдельные части и изобразим расчетные схемы отдельно для каждого тела. Определение реакций связей проведем с помощью теоремы об изменении кинетического момента и теоремы об изменении количества движения.
Тело №1: ![]()
![]()
Тело №2: 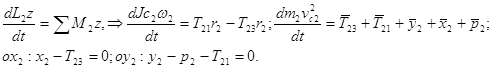
Тело №3: 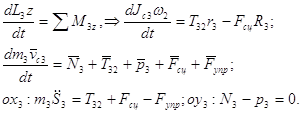
![]()
C учётом кинематических соотношений (1.7) полученную систему уравнений преобразуем к вид:
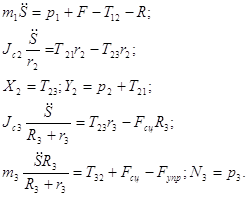
Решая эту систему, получаем выражение для определения реакций связей:
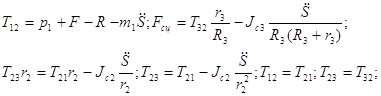
![]()
2. Построение алгоритма вычислений:
(2.1) Исходные данные:
![]()
(2.2) Вычисление констант:
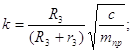
![]()
![]()
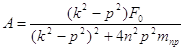
![]()
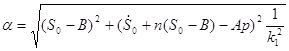
![]()
(2.3) Задание начального времени: t=0;
(2.4) Вычисление значений функций в момент времени t=0;

![]()
![]()
(2.5) Вычисление реакций связей:
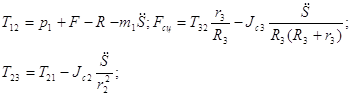
![]()
![]()
(2.6) Вывод на печать значений искомых функций в момент времени t;
(2.7) Определение значения времени на следующем шаге ![]()
(2.8) Проверка условия окончания цикла: ![]()
(2.9) Возврат к пункту (2.4).
3. Применение принципа Даламбера-Лагранжа и уравнения Лагранжа второго рода
3.1 Применение принципа Даламбера-Лагранжа
Общее уравнение динамике системы есть математическое выражение принципа Даламбера-Лагранжа.
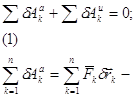
сумма элементарных работ всех активных сил на возможном перемещении системы;
![]() сумма элементарных работ всех инерции сил на возможном перемещении системы.
сумма элементарных работ всех инерции сил на возможном перемещении системы.
Изобразим на рисунке активные силы и силы инерции (рис.3)
Идеальные связи: ![]()
Не учитываем, и не отображаем на расчетной схеме, поскольку по определению работа их реакций на любом возможном перемещении системы равна 0.
Сообщим системе возможное перемещение.
![]()
Вычисляя последовательно элементарные работы активных сил и суммируя получим:
(2) ![]()
Найдём возможную работу сил инерции:
![]()
Запишем выражение для главных векторов и главных моментов сил инерции;
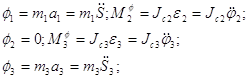
Используя кинематические соотношения (1.7), определим:
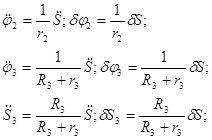
Теперь возможную работу сил инерции можно преобразовать к виду:
![]()
(3) ![]()
Далее подставляя выражения (2) и (3) в (1), т.е в общее уравнение динамики получаем
![]()
Поделив это уравнение на ![]() , получим дифференциальное уравнение вынужденных колебаний системы:
, получим дифференциальное уравнение вынужденных колебаний системы:
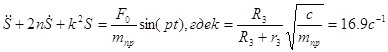
Анализ результатов
В данной курсовой работе мы исследовали динамическое поведение механической системы с использованием основных теорем и уравнений теоретической механики. Дифференциальное уравнение движения механической системы получено тремя способами. Во всех случаях коэффициенты ![]() , n, k получились одинаковыми и совпали с компьютерной распечаткой, что говорит об их правильности. В процессе решения дифференциального уравнения данной механической системы были получены законы движения первого груза, его скорость и ускорение в зависимости от времени t. На основании этих зависимостей были определены законы изменения всех остальных характеристик механической системы, в том числе и реакции связей.
, n, k получились одинаковыми и совпали с компьютерной распечаткой, что говорит об их правильности. В процессе решения дифференциального уравнения данной механической системы были получены законы движения первого груза, его скорость и ускорение в зависимости от времени t. На основании этих зависимостей были определены законы изменения всех остальных характеристик механической системы, в том числе и реакции связей.
Похожие работы
... груза, его скорости и ускорения, а также динамических реакций внешних и внутренних связей. Результаты расчетов: 5. Анализ результатов вычислений Математическая модель, описывающая поведение исследуемой механической системы, построена при следующих основных допущениях: ...
... полномочий. Оперативность структуры означает возможность реакции системы на изменения обстановки, временные показатели этой реакции и ее цену. Типичным примером организации как сложной системы является производственно-экономическая система (ПЭС). Основным видом производственно-экономических систем является предприятие. Приведем, применительно к промышленному предприятию, некоторые необходимые ...
... второй части курсовой работы и разработать проект с предложением соответствующих рекомендаций для эффективности его введения. 2 Анализ и оценка эффективности системы управления торгового предприятия (ИП Иванова А.А.) 2.1 Характеристика предприятия ИП Иванова А.А. Предприятие ИП Иванова А.А. находится в г. Шарыпово по адресу ул. Заводская, 8. Вблизи него располагается ...
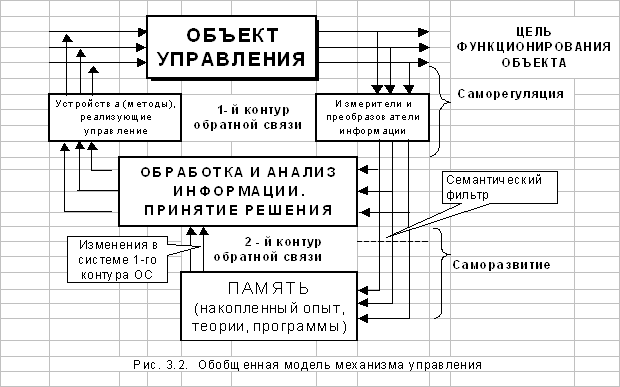
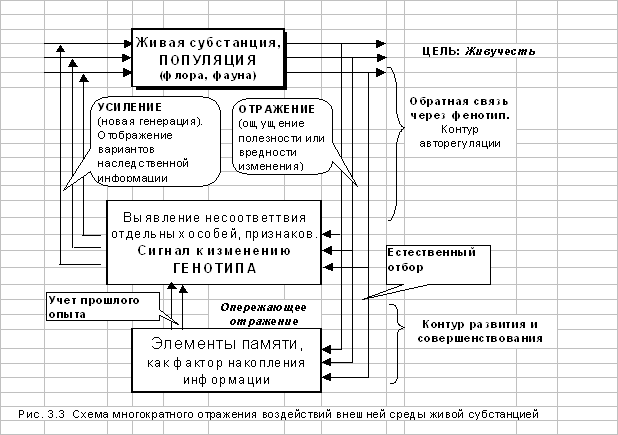
... Возникшие потребности в научно обоснованных методах и средствах управления нашли свое выражение в кибернетике - науке об управлении и системном анализе, особым предметом исследования которых являются сложные и очень сложные системы окружающего мира. 4.4 Организационные системы Традиционно современная кибернетика рассматривала, в основном, простые и сложные управляемые системы, для которых ...
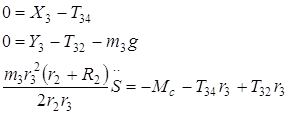
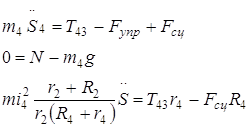
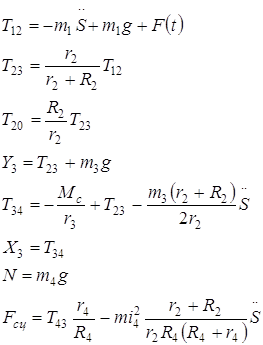
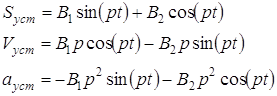
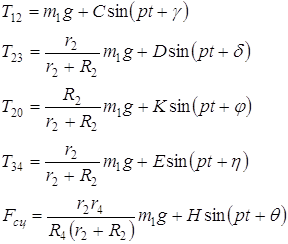





0 комментариев