КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

1.3 КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

Кинетостатический расчет, положенный в основу силового расчета механизма, базируется на принципе Д’Аламбера, который в общем случае движения звеньев механизмов, совершающих сложное плоское движение, позволяет решить задачу путем сведения сил инерции звеньев к главному вектору инерции F_i и к главному моменту сил M_i.

 (1.3.1)

Знак “-” означает, что вектор силы инерции направлен в сторону противоположную ускорению центра масс.

Массы звеньев рассчитываются с помощью формулы:

 (1.3.2)

где q = 0.1 кг/м,

l – длина звена.

m = P/g,

где P – вес звена (H),

g – ускорение свободного падения.

g = 9.8 м/с².

Также существует главный момент инерции звена, который приложен к центру масс звена и направлен в противоположную угловому ускорению звена сторону

 (1.3.3)

где  — момент инерции звена,

— угловое ускорение звена.

1.3.1 РАСЧЕТ СИЛ И ГЛАВНЫХ МОМЕНТОВ ИНЕРЦИИ ЗВЕНЬЕВ МЕХАНИЗМА

.

m_AB = 2,6 кг.

m_CA 0,008кг.

m_EF =0.0105кг.

m_DC=0.005кг

,

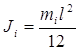Силы и главные моменты инерции приведены в таблице

222.3	0.89	0.48	0.5	0	0.89	0.18 0.171

Таблица 1.3.1. Рассчитанные значения сил и моментов инерции звеньев механизма

1.3.2 ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В КИНЕМАТИЧЕСКИХ ПАРАХ

Силовой анализ механизма начинаем с группы Ассура 3-5, наиболее удалённой от ведущего звена. Связи в шарнирах заменяются реакциями и .

В шарнире F реакция неизвестна по модулю и направлена по горизонтали. Обозначим в точке  силу инерции. Обозначим также вес звена FE и вес ползуна Р.

Сумма моментов относительно точки F равна нулю:

 (1.3.4)

где ,— плечи соответствующих силы и веса

Находим :

 (1.3.5)

Составляем векторное уравнение:

 (1.3.6)

С учётом этого уравнения строим замкнутый силовой многоугольник. На чертеже выбираем полюс . От него проводим вектор произвольной длины по направлению силы .Вычисляем масштабный коэффициент:

 (1.3.7)

Далее к вектору  достраиваем другие составляющие уравнения (1.3.6), рассчитывая длину векторов при помощи масштабного коэффициента.

Определяют реакции в кинематической паре 2-4. Реакции в шарнирах A и D нужно разложить на составляющие по направлению осей  и , и перпендикулярные им:  и . Тангенциальные составляющие можно найти, если записать уравнение суммы моментов каждого звена относительно точки С.

Условия равновесия звеньев 2 и 3 соответственно:

 (1.3.9)

  (1.3.10)

 

Рассмотрим уравнение равновесия группы в целом. Запишем векторное уравнение равновесия этой группы:

 (1.3.11)

В этом уравнении все составляющие, кроме , известны по модулю и по направлению. Нужно построить замкнутый силовой многоугольник, откладывая последовательно векторы сил.

 (1.3.12)

Рассмотрим уравнение равновесия группы в целом. Запишем векторное уравнение равновесия этой группы:

 (1.3.13)

В этом уравнении все составляющие, кроме , известны по модулю и по направлению. Нужно построить замкнутый силовой многоугольник, откладывая последовательно векторы сил.

Теперь определим уравновешивающую силу и уравновешивающий момент, действующий на кривошип AB.

На кривошип AB действует шатун силой . Считается, что сила  приложена перпендикулярно звену AB. В этом случае уравнение моментов всех сил, приложенных к кривошипу относительно точки B, имеет вид:

 (1.3.12)

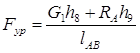 (1.3.13)

 

 (1.3.14)

 

Найденные при силовом анализе механизма величины представлены в таблице 1.4.

57	48	65	0.22	0.6	0.8	0.79	0.7	0.9	73	1.9

Таблица 1.4. Силовой анализ механизма